Задачи. Олимпиадные задачи по математике за 6 класс - Погребникова Алена. Арифметика На карточках записаны цифры 1, 2, Из этих карточек составлены числа и записано неверное равенство. Покажите, как, переместив только одну карточку, сделать равенство верным. 1
 Скачать 0.53 Mb. Скачать 0.53 Mb.
|
|
Задача 10: Докажите, что из 26 различных натуральных чисел, не превосходящих 50, всегда можно выбрать два числа, одно из которых делится на другое. Решение: Разобьем числа на «цепочки»: 1-2-4-8-16-32; 3-6-12-24-48; 5-10-20-40; … 25-50; 27; … 49 Иначе говоря, каждая цепочка однозначно задана своим наименьшим нечётным делителем. Цепочек всего 25, поэтому какие-то два из 26 чисел попадут в одну и ту же цепочку. Задача 11: Попробуйте обобщить предыдущую задачу, если вместо 50 в условии будет стоять произвольное чётное число 2N. (Какое число должно стоять вместо числа 26?) Решение: N + 1 Задача 12: Дано 20 различных натуральных чисел, меньших 70. Рассматриваются всевозможные их попарные разности (из большего числа вычитают меньшее). Докажите, что среди них всегда найдутся четыре одинаковых. Решение: Простая оценка числа попарных разностей не дает требуемого результата. Правильная оценка строится так: будем считать, что числа упорядочены по возрастанию, и рассмотрим числа a2 – a1, a3 – a2, …, a20 – a19. Сумма этих 19 натуральных чисел равна a20 – a1, то есть меньше 70 – 1. Но если предположить, что среди них нет четырёх равных, то там не более трёх единиц, трёх двоек, …, трёх шестерок и еще одно число, не меньшее 7. Сумма таких чисел не меньше, чем 3 • (1 + 2 + 3 + 4 + 5 + 6) + 7 = 70. Получили противоречие, доказывающее, что четыре равных разности найдутся даже среди выписанных 19 разностей соседних чисел. Задача 13: В последовательности 2, 0, 0, 0, 2, 2, 4,…каждый член, начиная с пятого, равен последней цифре суммы предшествующих четырёх членов. а) Встретятся ли в этой последовательности еще раз подряд 4 цифры 2, 0, 0, 0? б) Встретятся ли в ней четыре подряд цифры 0, 0, 8, 2 ? Решение: а) Да. б) Да. Последовательность рано или поздно зациклится, потому что четверка последовательных цифр однозначно определяет следующую цифру. При этом последовательность обратима с любого места, то есть в ее период входят все цифры, включая самые первые. Цифры 0,0,8,2 встретятся в ней как раз перед вторым появлением четверки 2,0,0,0, потому что если продлить вправо 0,0,8,2, то последовательно получим 0,0 и 0. Задача 1: Коридор длины 6 м покрыт тремя трёхметровыми ковровыми дорожками, причём нигде дорожки не лежат в три слоя. Докажите, что какие-то две из них перекрываются не меньше, чем на 1,5 м. Решение: Занумеруем дорожки слева направо. Закрасим все такие участки, где первая дорожка перекрывается со второй, а вторая с третьей. Суммарная длина таких перекрытий равна 3 м: три дорожки длины 9 м должны уместиться на коридоре длины 6 м. Следовательно, какое-то из этих трёх перекрытий не меньше 1,5 м (а какое-то другое – не больше 1,5 м). Задача 2: Окружность длины 6 м покрыта тремя трёхметровыми дугами, причём никакие три дуги не имеют общих точек. Докажите, что какая-то пара дуг имеет пересечение не меньше, чем 1 м. Задача 3: В комнате площадью 6 кв.м постелены на полу три ковра площади 3 кв.м каждый. Верно ли, что какие-нибудь 2 из них пересекаются по площади, не меньшей 1 кв.м.? Решение: Будем считать, что сначала на пол положен первый ковёр, затем второй, затем третий, то есть ковёр с меньшим номером не может лежать на ковре с большим номером. Суммарная площадь ковров равна 9, площадь ковров, лежащих непосредственно на полу, не больше 6, значит, часть ковров площадью не меньше 3 лежит на других коврах. Эта площадь складывается из: 1) части третьего ковра, лежащей непосредственно на втором, 2) части третьего ковра, лежащей непосредственно на первом 3) части второго ковра, лежащей на непосредственно на первом. Отсюда следует, что одна из этих частей не меньше 1. Задача 4: В комнате площадью 6 кв.м постелены на полу три ковра площади S кв.м каждый. Известно, что S > 2. Докажите, что какие-нибудь 2 из них пересекаются по площади, не меньшей S – 2 кв.м. Задача 5: В комнате площадью 6 кв.м на полу постелены 4 ковра площади 2 кв.м каждый. Верно ли, что какие-то два из них обязательно перекрываются по площади, не меньшей 1 кв.м? Решение: Нет, неверно. Контрпример строится очень легко. Задача 6: Внутри квадрата со стороной 1 расположены 4 прямоугольника, площадь каждого из которых не менее 1/2. Докажите, что хотя бы два из них имеют общую часть площади не менее 1/6. Задача 7: На кафтане площади 1 расположены 4 заплаты, площадь каждой из которых не менее 5/8. Докажите, что какие-то две из них имеют общую часть площади не менее 1/3. Решение: «Излишек» площади состоит из 6 ( = 4 • 3/2) попарных пересечений (при этом возможны тройные и четверные пересечения). Обозначим через S1 площадь, покрытую только один раз, S2 – площадь двойных пересечений, через S3 – площадь тройных и через S4 – площадь четверных пересечений. Сумма всех площадей попарных пересечений равна S2 + 3S3 + 6S4. С другой стороны, по условию S1 + 2S2 + 3S3 + 4S4 ≥ 4 • 5/8 = 2.5. Умножая это неравенство на 2 и вычитая очевидное условие 3(S1 + S2 + S3 + S4) ≤ 3 (квадрат не обязательно покрыт целиком!), получаем неравенство – S1 + S2 + 3S3 + 5S4 ≥ 2. Следовательно, S2 + 3S3 + 6S4 ≥ 2 и какое-то из попарных пересечений заплат не меньше 2/6. Задача 8: На спортивные соревнования в ЛМШ ходили 220 школьников. При этом некоторые из них участвовали в чемпионатах, а остальные были зрителями. В легкоатлетической эстафете приняли участие 30 человек, в соревнованиях по волейболу – 26, пионерболу – 32, футболу – 31, шахматам – 28 и теннису – 36 человек. 53 школьника приняли участие более чем в одном соревновании; из них 24 школьника участвовали 3 или более раз, 9 школьников – не менее 4 раз и 3 школьника – даже 5 раз (в последнюю тройку входит и один чудак, который выступал во всех шести соревнованиях). Сколько из школьников были зрителями? Решение: Это классическая задача на «круги Эйлера» и формулу включений и исключений – в ней необходимо тщательно разобраться с составом участников соревнований. В сумме в них были 30 + 26 + 32 + 31 + 28 + 36 = 183 школьника. Число школьников, игравших хотя бы один раз, равно 183 – 53 – 24 – 9 – 3 – 1 = 93. Оставшиеся 127 школьников были зрителями. Задача 9: На кафтан площади 1 поставлены 5 заплат. Площадь каждой из них равна 1/2. Докажите, что найдутся две заплаты, пересекающиеся по площади не менее 1/5. Решение: Обозначим через xk площадь части кафтана, покрытую ровно k заплатами (k = 0, 1, …, 5). По условию площадь кафтана равна 1, а сумма площадей заплат – 5/2: S0 = x0 + x1 + x2 + x3 + x4 + x5 = 1,S1 = x1 + 2x2 + 3x3 + 4x4 + 5x5 = 5/2. Сумма площадей всех 10 попарных пересечений заплат равна S2 = x2 + 3x3 + 6x4 + 10x5. Оценим ее: S2 ≥ – 3x0 – x1 + x2 + 3x3 + 5x4 + 7x5 = 2S1 – 3S0 = 2, поэтому хотя бы одно из 10 попарных пересечений будет по площади не меньше 2/10. Равенство возможно, только если x0 = x1 = x4 = x5 = 0 и все 10 попарных пересечений равны по площади! Задача 10: На кафтане площади 1 имеется 5 заплат площади 1/3. Докажите, что найдутся такие две заплаты, площадь общей части которых не меньше 1/15. Задача 11: На кафтане площади 1 имеется 9 заплат площади 1/5. Докажите, что найдутся такие две заплаты, площадь общей части которых не меньше 1/45. Математические игры Задача 1: В двух кучках лежат предметы, по 100 предметов в каждой. За ход разрешается взять произвольное количество предметов, но только из одной кучки. Проигрывает тот, кто не может сделать очередной ход. Найдите выигрышную стратегию для второго игрока. Решение: Второму игроку достаточно повторять ходы первого, но только в другой кучке. Таким образом, только после ходов второго в количество предметов в кучках становится равным, следовательно, ситуация, когда в обеих кучках не останется ни одного предмета, также может наступить только после хода второго, а, значит, он не проиграет. Поскольку с каждым ходом количество предметов в кучках уменьшается, игра закончится, и так как второй не проиграет – он выиграет. Задача 2: В трёх кучках лежат предметы, по 100 предметов в каждой. За ход разрешается взять произвольное количество предметов, но только из одной кучки. Проигрывает тот, кто не может сделать очередной ход. Найдите выигрышную стратегию для первого игрока. Решение: Забирая все предметы из одной кучки, первый сводит игру к игре «две кучки по 100», в которой он играет уже вторым. Задача 3: Два миллионера по очереди кладут пятаки на круглый стол, так, чтобы они не накладывались друг на друга. Проигрывает тот, кто не может сделать хода. Как надо играть миллионеру, который кладёт первый пятак, чтобы наверняка выиграть? Решение: Выигрывает первый. Первый ход – положить пятак в центр стола, и дальше симметрия. Задача 4: Двое по очереди разламывают шоколадку. За один ход разрешается сделать прямолинейный разлом любого из имеющихся кусков вдоль углубления. Проигрывает тот, кто первым отломит дольку 1 × 1. Кто выигрывает при правильной игре, если шоколадка имеет размеры а) 10 × 10; б) 10 × 13. в) шоколадка 10 × 13, но первый получивший дольку 1 × 1 выигрывает. Решение: Всюду выигрывает второй, разделив шоколадку на две, и далее действуя симметрично. В пункте в) надо играть симметрично до предпоследнего момента. Задача 5: Двое по очереди ставят шахматных слонов в клетки доски 8 × 8 так, чтобы слоны не били друг друга. Проигрывает тот, кто не может сделать ход. Кто выигрывает при правильной игре, и как ему при этом нужно играть? Решение: Выигрывает второй. Симметрия относительно вертикальной оси или относительно центра. Задача 6: У ромашки а) 12 лепестков; б) 11 лепестков. За ход разрешается оторвать либо один лепесток, либо два рядом растущих лепестка. Проигрывает тот, кто не может сделать хода. Решение: В обоих случаях выигрывает второй. Своим первым ходом он разбивает лепестки на две одинаковых группы, а дальше действовать симметрично. В а) проходит и тривиальная центрально-симметричная стратегия. Задача 7: Доска 8 × 8. За ход можно положить доминошку на любое свободное место. Проигрывает тот, кто не может сделать очередной ход. Решение: Выигрывает второй, стратегия – центральная симметрия. Задача 8: В каждой клетке доски а) 11 × 11 б) 11 × 12 в) 12 × 12 стоит шашка. За ход разрешается снять с доски любое количество подряд идущих шашек либо из одного вертикального, либо из одного горизонтального ряда. Выигрывает снявший последнюю шашку. Решение: В а) выигрывает первый. Например, первым ходом он снимает центральную шашку и дальше действовует центральносимметрично. В б) первым ходом нужно снять всю центральную (шестую) вертикаль, а дальше действовать осесимметрично. (Эта же стратегия проходит и в задаче а)). И, наконец, в в) можно сразу действовать центральносимметрично, поэтому выигрывает второй. Задача 9: Для игры «щелк» требуется прямоугольная шоколадка (в этой задаче – шоколадка 8 × 8). За ход разрешается съесть произвольную дольку и все находящиеся справа и сверху от неё. Проигрывает тот, кто съедает левую нижнюю дольку. Решение: Выигрывает первый. Он должен первым ходом съесть квадрат 7 × 7, и далее действовать симметрично. Задача 10: Двое играют в следующую игру: первый выбирает любое поле на доске 8 × 8, ставит туда короля и делает ход (король может ходить в соседние и соседние по диагонали клетки), при условии, что на эту клетку раньше никто не вставал. Проигрывает тот, кто не может сделать ход. Кто выигрывает при правильной игре? Решение: Выигрывает второй. Клетки разбиваются на пары стоящих рядом (например на доминошки), и как только первый поставил короля на одну из клеток пары, второй ходит на другую. Задача 1: Игра начинается с числа 60. За ход разрешается уменьшить имеющееся число на любой из его делителей. Проигрывает тот, кто получит ноль. Решение: Во-первых, заметим, что эта игра всегда заканчивается победой одного из игроков: числа на доске постоянно уменьшаются, поэтому рано или поздно на доске окажется число 0. Теперь докажем, что выигрывает первый. Своим ходом он всегда может забирать 1, оставляя второму нечётное число. Второй должен отнять от нечётного числа какой-нибудь его делитель, а поскольку все делители нечётных чисел нечётны, то в результате после хода второго на доске опять окажется чётное число. Таким образом, первый игрок всегда сможет сделать ход, то есть он не может проиграть. Следовательно (см. первое замечание), проиграет второй. Задача 2: Волк и Заяц играют в следующую игру: на доске написано некоторое натуральное число с ненулевой последней цифрой. Ход состоит в том, что из числа вычитают какую-нибудь его ненулевую цифру и пишут результат вместо старого числа. Выигрывает тот, кто первым получит нуль. Решение: Первый игрок постоянно вычитает из числа его последнюю (ненулевую!) цифру. Задача 3: Имеется две кучи конфет: в первой – 40, во второй – 45. За ход нужно одну кучу съесть, а другую разделить на две (не обязательно равные). Проигрывает тот, кто не может сделать ход. Решение: В этой игре выигрывает первый игрок. Он всегда съедает нечётную кучку, а чётную делит на две нечётных – в результате после его хода оказываются две нечётных кучки, а после хода второго – снова одна нечётная и одна чётная кучка. Единственная позиция, в которой невозможно сделать ход – позиция (1,1), которая могла получиться только после хода первого игрока. Задача 4: Имеется две кучи конфет: в первой – 100, во второй – 201. За ход разрешается съесть из одной кучки любое число конфет, являющееся делителем количества конфет в другой кучке. Выигрывает тот, кто съедает последнюю конфету. Решение: И здесь выигрышными являются позиции, в которых обе кучки содержат нечётное число конфет. Первый игрок должен своим ходом взять 1 конфету из первой кучки. Задача 5: Два игрока ставят по очереди числа вместо звездочек в следующей системе равенств: 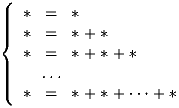 (в последнем равенстве справа 8 слагаемых). Второй игрок выигрывает, если все равенства выполняются, в противном случае выигрывает первый. Решение: Эта задача кодируется игрой про 8 шашек, стоящих на диагонали шахматной доски. Задача 6: Имеется полоска клетчатой бумаги длиной 10 клеток. В крайней правой ее клетке стоит шашка (рис. 1). Двое играющих по очереди передвигают ее влево на одну или две клетки. Проигрывает тот, кому некуда ходить. 6cm Рис 1. Решение: Представим себе, что шашка уже дошла до крайней левой клетки, помеченной на рис. 1 цифрой 0. Понятно, что в этом случае проиграл тот, чья очередь ходить (назовем его очередником), потому что ходить ему некуда. А вот если шашка стоит на клетках 1 или 2 то очередник одним ходом сдвинет ее на клетку 0 и выиграет. Отметим клетку 0, где очередником быть невыгодно, минусом, а выгодные для очередника клетки 1 и 2 – плюсами (рис. 2). 6cm Рис 2. 6cm Рис 3. Теперь посмотрим, каково быть очередником, когда шашка стоит на клетке 3? Если сдвинуть шашку на одну клетку, она окажется на клетке 2, а если на две – на клетке 1. Обе клетки выгодны для очередника, да только очередником будет уже не тот, кто ходил, а его партнер. Он и выиграет. Получается, что клетка 3 для очередника невыгодна, а клетки 4 и 5 выгодны: с них очередник одним ходом переводит шашку на клетку 3, и его партнер, став очередником, оказывается у разбитого корыта. Продолжая в том же духе, нетрудно показать, что клетка 6 невыгодна для очередника, клетки 7 и 8 – выгодны, а клетка 9 – снова невыгодна (рис. 3). Стало быть выигрывает второй игрок. Задача 7: Кто выигрывает в игре Баше, если длина полоски составляет 11 клеток? 12 клеток? 13 клеток? 2000 клеток? Решение: Как видно из решения предыдущей задачи, невыгодные для очередника позиции – это клетки, номера которых имеют остаток 1 при делении на 3. Поэтому на полоске длиной 12 клеток выигрывает второй игрок, а на полосках длин 11, 13 и 2000 клеток – первый. Задача 8: Изменим правила игры Баше: теперь за один ход можно сдвигать шашку на 1, 2, 3, 4 или 5 клеток, а длина полоски – 13 клеток. Решение: Нарисуем эту полоску и, как в предыдущей задаче, отметим на ней плюсами и минусами клетки, выгодные и невыгодные для очередника. Получается, что невыгодные для очередника клетки (то есть клетки, на которые надо ходить, чтобы выиграть) имеют остаток 1 при делении на 6. Задача 9: А теперь в игре Баше можно сдвигать шашку на 3, 6, 9 или 12 клеток, а длина полоски – 40 клеток. Задача 10: Проанализируйте игру Баше, где можно сдвигать шашку на 1, 3 или 4 клетки, а длина полоски – 15 клеток. А что можно сказать про случай, если длина полоски – 2000 клеток? Задача 1: Имеется 40 конфет. Двое по очереди едят от одной до шести из них. Выигрывает съевший последнюю конфету. Решение: А что это, как не игра Баше? Первым ходом нужно съесть 5 конфет. Задача 2: Имеется 40 конфет. Двое по очереди едят от 1 до 6 из них. Тот, кто съел последнюю, проигрывает. Решение: Это тоже игра Баше, только цель в ней – достичь не нуля конфет, а одной конфеты! Все выигрышные позиции сдвинуты на 1 относительно «стандартной» игры. Первый игрок должен первым ходом съесть 4 конфеты. Задача 3: В 6-й класс ЛМШ приехало 50 школьников. За ход разрешается съесть двух, четверых или семерых из них. Проигрывает тот, кто не может сделать ход. Решение: Выигрышными здесь являются все «позиции», в которых число школьников больше 3 и не кратно 3, а также «позиции» 2 и 3. Работает стратегия «ставь на минус!» – первым ходом игрок должен съесть двух школьников и оставить 48. Затем на каждый ход 2 он отвечает ходом 7, а на каждый ход 4 или 7 – ходом 2. Так он действует до тех пор, пока число школьников не станет равно 6, 9 или 12. В позиции «12» на ход 7 надо ответить ходом 4 (соответственно, на ход 4 нужно ответить ходом 7), а на ход 2 – также ходом 4. В позиции «9» на ход 7 отвечаем ходом 2 (и наоборот), а на ход 4 – тоже ходом 4. Наконец, в позиции «6» возможны только ходы 4 и 2, поэтому все очевидно. Задача 4: В чашке сидит 105 микробов. За ход разрешается вытащить 2, 3 или 5 микробов. Проигрывает тот, кто не может сделать очередной ход. Решение: Проигрышными являются позиции вида 7k и 7k + 1. Поскольку 105 – одна из таких позиций, то в игре выигрывает второй игрок. Задача 5: Конь стоит на поле a1. За ход разрешается передвигать коня на две клетки вправо и одну клетку вверх или вниз, или на две клетки вверх и на одну вправо или влево. Проигрывает тот, кто не может сделать ход. Кто выигрывает при правильной игре? Решение: Проигрывает первый игрок. На доске проигрышными клетками являются только a1, c3, c4, d3, d4, c7, c8, d7, d8, g3, g4, h3, h4, g7, g8, h7, h8. Задача 6: В кучке n спичек. За ход нужно взять от 1 до 3 спичек, но не столько, сколько только что взял противник. Тот, кто не может сделать ход, проигрывает. Кто выигрывает при правильной игре сторон а) при n = 12 б) при n = 13? Решение: Для анализа игры нужно понять, что она ведется на поле n × 3, где номер строки соответствует величине последнего хода, сделанного соперником. Задача 7: В куче – n спичек, из них 3 – обломанные, остальные – целые. За ход можно взять 1, 2 или 3 спички, но обломанные можно брать только когда кончились целые. Тот, кому досталось меньше обломанных спичек, выплачивает разницу в их числе другому. Кто победит и с каким счетом а) при n = 13; б) при n = 14? Задача 8: Имеется две кучи по семь апельсинов. За ход разрешается съесть один апельсин из любой кучки или по одному апельсину из каждой кучки. Проигрывает тот, кто не сможет сделать ход. Задача 9: Король стоит на поле a1. За один ход разрешается сдвинуть его на одну клетку вверх, одну клетку вправо или одну клетку по диагонали вправо-вверх. Выигрывает тот, кто поставит короля на поле h8. Решение: Эти две игры кодируются друг дружкой. Задача 10: .7mm 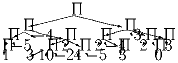 В начале игры фишка стоит на верхней позиции П. Игроки по очереди передвигают ее на одну позицию вниз по линиям. Игра заканчивается, когда фишка попадает на число. После этого второй выплачивает первому столько тугриков, каково это число (если число меньше 0, то на самом деле выплачивает первый второму). Сколько тугриков будет выплачено при наилучшей игре сторон, и какой игрок их получит? Решение: Второй выплатит первому 2 тугрика. Задача 11: В трёх кучках лежит по 7 камней. За ход можно взять любое количество камней, но только из одной кучки. Выигрывает взявший последний камень. а) Кто выигрывает в этой игре, если в нее играют 2 человека? б) Докажите, что если в эту игру играют трое, то двое из них могут сговориться и обыграть третьего. Задача 12: В коробке лежат 300 спичек. За ход можно взять из коробка не более половины имеющихся в нем спичек. Проигрывает тот, кто не может сделать ход. Решение: Проигрышными позициями («минусами») являются 1, 3, 7, 15, 31, 63, 127 и 255. Задача 13: На столе лежат 9 карточек, на которых написаны натуральные числа от 1 до 9. Двое по очереди откладывают в сторону по одной карточке. Проигрывает тот, после хода которого сумма чисел на отложенных карточках станет больше 25. Решение: Первый берет карточку с числом 5, а затем дополняет ходы противника до 10. Задача 1: Найдите выигрышную стратегию для первого игрока в игре «щёлк» на шоколадке 2 × 100. Решение: Выигрышные позиции – шоколадки, со столбцами длинами n + 1 и n. Задача 2: Проанализируйте игру «щёлк» на огрызке шоколадки из трёх строчек: 2, n и n + 2 дольки. а) Кто выигрывает при n = 2,3,4,5 б) n – произвольное. Задача 3: Игра в «двойные шахматы» ведется также, как и в обычные, только игроки делают по 2 хода за раз. Докажите, что в этой игре у второго игрока не может быть выигрышной стратегии. Решение: Передача хода – ход конём туда-обратно, в результате чего позиция не изменится. Знатоки шахматных правил могут заметить, что на самом деле ситуация в игре всё же не вполне симметрична, так как есть, наример, правило троекратного повторения позиции (и правило 50 ходов). Полезно подумать, как можно ответить на эти возражения. Задача 4: Докажите, что в игре «щёлк» у первого игрока есть выигрышная стратегия на любой прямоугольной шоколадке, в которой больше одной дольки (предъявлять стратегию не обязательно). Решение: Вничью игра закончиться не может. Предположим, что выигрышная стратегия есть у второго игрока. Долька, находящаяся в правом верхнем углу съедена в любом случае после первого хода. Если у второго есть выигрышная стратегия, то у него есть выигрышный ответный ход на ход первого, состоящий в поедании только правой верхней дольки. Но этот выигрышный ход первый может с тем же успехом сделать сам с самого начала, а далее воспользоваться выигрышной стратегией второго! (А так ли получается, если в шоколадке всего одна долька?) Задача 5: На бесконечной доске двое играют в крестики-нолики. Кто поставит пять своих в ряд – по вертикали или горизонтали – выигрывает. Докажите, что при правильной игре первый не проигрывает. Задача 6: На доске написано число 2. За ход можно к записанному числу прибавить один из его делителей отличный от самого этого числа. Проигрывает тот, кто получит число большее 1000. Докажите, что у первого игрока есть выигрышная стратегия. Решение: После первых двух ходов всегда получается число 4. Из него можно получить как 5, так и 6, но из 5 можно получить только 6. Следовательно, после числа 4 можно осуществить передачу хода в зависимости от того, выигрышным или проигрышным является число 6. Задача 7: Двое играют в следующую игру: первый выбирает любое поле на доске 8 × 8, ставит туда а) короля; б) коня и делает ход этой фигурой, причём разрешается ходить только на те клетки, на которые раньше никто не вставал. Далее игроки ходят по очереди. Проигрывает тот, кто не может сделать ход. Решение: Выигрывает второй. Клетки разбиваются на пары стоящих «ходом короля (коня)», и как только первый поставил короля (коня) на одну из клеток пары, второй ходит на другую. Задача 1: Может ли в месяце быть 3; 4; 5; 6 воскресений? Задача 2: Может ли в году быть 51; 52; 53; 54 воскресенья? Задача 3: Может ли сумма цифр трёхзначного числа быть равной 22? А равной 28? Задача 4: Может ли произведение цифр трёхзначного числа быть равно 22? 28? 350? 730? Задача 5: Позавчера Васе было 11 лет, а в следующем году исполнится 14. Может ли такое быть? Задача 6: Двое близнецов родились с интервалом в 10 минут. Когда спустя 7 лет они готовились идти в первый класс, их спросили, сколько им лет. «Мне вчера исполнилось семь», – гордо ответил один. «А мне семь исполнится только завтра», – признался второй. Как такое могло быть? Решение: Они родились в ночь с 28 февраля на 1 марта невисокосного года, а в школу поступали в високосном году. Вопрос был задан 29 февраля. Задача 7: Можно ли в прямоугольную таблицу поставить числа так, чтобы в каждом столбце сумма была положительна, а в каждой строке – отрицательна? Задача 8: Можно ли в таблицу 4 × 4 поставить числа – 1, 0 и 1 так, чтобы все 8 сумм чисел в строках и столбцах были различными? Задача 9: Можно ли в прямоугольной таблице расставить натуральные числа так, чтобы в каждом столбце сумма чисел была больше 100, а в каждой строке – меньше 5 ? Задача 10: Может ли и сумма, и произведение нескольких натуральных чисел быть равными а) 999? б) 1999? Решение: а) Да. Например, это числа 111, 9 и много-много единиц. б) Нет. 1999 – простое число, так что среди множителей непременно присутствует само это число, а тогда сумма больше 1999. Задача 11: Площадь прямоугольника меньше 1 кв.м. Может ли его периметр быть больше 1 км? Решение: Да, пусть стороны равны 500 м и 1/1\,000 м. Задача 12: На балу было юношей и девушек поровну, было 10 танцев и каждый раз танцевали все. а) Могло ли получиться, что каждый юноша каждый следующий танец танцевал либо с более красивой, либо с более умной девушкой? Решение: Пусть на балу 3 юноши и 3 девушки А, Б и В, причём красота возрастает в порядке АБВ, а ум – в порядке БВА. Юноши чередуют девушек по кругу в порядке АБВ. Задача 13: Сумма положительных чисел больше 10. Может ли сумма их квадратов быть меньше 1? Решение: Да. Возьмем 1001 число, все равны 1/100, тогда их сумма равна 10.01, а сумма квадратов – 1\,001/10\,000. Задача 14: На занятии Вася, Леня и Стас решили все задачи. Может ли оказаться, что Стас большинство задач решил раньше Лени, Леня – большинство раньше Васи, а Вася – большинство раньше Стаса? Решение: Например, задач всего три, первую задачу решил сперва Стас, потом Леня, потом Вася; вторую – Леня, Вася, Стас; третью – Вася, Стас, Леня. Задача 15: Фирма проработала год, подсчитывая свою прибыль каждый месяц. Каждые два подряд идущих месяца суммарная прибыль была отрицательной. а) Может ли суммарная прибыль за весь год быть положительной? б) А за первые 11 месяцев? Решение: а) Нет. Разбиваем 12 месяцев на пары, складываем и видим, что суммарная прибыль тоже должна быть отрицательной. б) Да: представим, что каждый нечётный месяц фирма работала с прибылью + 100, а в каждом чётном месяце прибыль равнялась – 101. Задача 16: В однокруговом футбольном турнире за победу давали 2 очка, за ничью 1 очко, за поражение 0 очков. «Спартак» одержал больше всех побед. Мог ли он набрать меньше всех очков? Решение: Да. Пусть Спартак одержал победу лишь однажды, а остальные матчи проиграл. Все матчи, в которых Спартак не участвовал, завершились вничью. Если в турнире участвовало не меньше пяти команд, то у Спартака меньше всех очков. Задача 17: Можно ли на шахматной доске расставить а) 9 ладей; б) 14 слонов так, чтобы они не били друг друга? Решение: Нельзя в обоих пунктах. Задача 18: Какое наибольшее число ладей (слонов, королей, ферзей, коней) можно расставить на доске так, чтобы они не били друг друга? Решение: 8 (12, 32, 8, 32) Задача 19: У шахматной доски выпилены а) угловая клетка; б) две противоположные угловые клетки; в) две клетки разного цвета. Можно ли такую испорченную доску распилить на двуклеточные прямоугольники? Решение: в) Обойдем шахматную доску ладьей по циклу. Выброшенные клетки разного цвета разобьют цикл на два куска чётной длины, и каждый кусок режется на пары соседних клеток. Задача 20: Из 4 одинаковых с виду монет одна фальшивая (легче настоящей). Можно ли наверняка найти ее за одно взвешивание на чашечных весах без гирь? Решение: Нельзя, поскольку при невезении после взвешивания останутся 2 подозрительные монеты. Задача 21: На сковороде могут одновременно жариться 2 котлеты. Каждую надо обжарить с обеих сторон, причём для обжаривания одной стороны требуются 2 минуты. Можно ли поджарить 3 котлеты быстрее, чем за 7 минут? Решение: Да. Через две минуты одну котлету переворачиваем, а вторую снимаем и вместо нее кладем третью. Через четыре минуты снимаем первую котлету, вместо нее кладем дожариваться вторую (на вторую сторону), а третью котлету переворачиваем. Через шесть минут котлеты готовы. Задача 22: В магазин привезли платья трёх цветов и трёх фасонов. Всегда ли можно выбрать для витрины 3 платья, чтобы были представлены все цвета и все фасоны? Решение: Не всегда. Например, если есть три красных платья трёх фасонов, и еще синее и зеленое платье первого фасона, то выбрать требуемым образом нельзя. Задача 1: На двух кустах сидело 25 воробьев. После того как с первого куста перелетело на второй 5, а со второго улетело 7 воробьев, то на первом кусте осталось вдвое больше воробьев, чем на втором. Сколько воробьев было на каждом кусте первоначально? Решение: Пусть x – количество воробьёв на первом кусте. Тогда x – 5 = 2 × (25 – x – 7 + 5). Решаем, и получаем, что x = 17. Задача 2: Золотоискатель Джек добыл 9 кг. песка. Сможет ли он за три взвешиванимя отмерить 2 кг песка с помощью двухчашечных весов а) с двумя гирями – 200 г и 50 г; б) с одной гирей 200 г? Решение: Сможет в обоих пунктах а) сначала надо без гирь отмерить 4 кг 500 г и 2 кг 250 г, а третьим взвешиванием при помощи гирь и отмеренного веса 2 кг 500 г взвесить 2 кг. б) При помощи гири взвесим 4.400 и 4.600, потом разделим 4.400 на две равные части по 2.200 и, наконец, отвесим ровно 2 кг. Задача 3: Часы показывают час дня. Найти ближайший момент времени, когда часовая и минутная стрелка совпадут. Решение: Это произойдет через 1/11 часа. Задача 4: Из 100 туристов, отправляющихся в заграничное путешествие, немецким языком владеют 30 человек, английским – 28, французским – 42. Английским и немецким одновременно владеют 8 человек, английским и французским – 10, немецким и французским – 5, всеми тремя языками – 3. Сколько туристов не владеют ни одним языком? Решение: только английским владеет 13 человек, только французским – 30, только немецким – 20 человек. 20 человек не знают ни одного из этих языков. Задача 5: Три человека выписали по 100 различных слов. После этого слова, встречающиеся не менее двух раз, вычеркнули. В результате у одного осталось 45 слов, у другого – 68, а у третьего – 54. Докажите, что по крайней мере одно слово выписали все трое. Решение: Если бы это было не так, то сумма всех попарных пересечений содержала бы чётное число слов. Задача 6: Оксана Николаевна раздавала фумигаторы для шести отрядов. Каждому отряду она давала половину всех имеющихся у нее фумигаторов и еще полфумигатора. Оксана Николаевна раздала все фумигаторы. Сколько их всего было? Решение: 63. Задача 7: На доске написаны 10 единиц и 10 двоек. За ход разрешается стереть две любые цифры и, если они были одинаковыми, написать двойку, а если разными – единицу. Если последняя оставшаяся на доске цифра – единица, то выигрывает первый игрок, а если двойка – то второй. Докажите, что игрок, который ходит вторым, всегда выигрывает. Решение: Чётность количества единиц не меняется. Задача 8: Каких натуральных чисел, меньших 200,000, больше: тех, которые делятся на 8 и не делятся на 9, или тех, которые делятся на 9 и не делятся на 8? Решение: Первых. Добавим и к тем, и к другим все числа, кратные 72. Тогда вопрос превратится в такой: каких чисел больше – тех которые делятся на 8 или тех, которые делятся на 9? Ответ на этот вопрос очевиден. Задача 1: На озере расцвела одна лилия. Каждый день число ее цветков удваивалось, а на 20-й день всё озеро покрылось цветами. На который день покрылась цветами половина озера? Решение: Начнём с конца. Пусть сегодня половина озера покрылась цветами. Через сколько дней покроется всё озеро? Завтра! И это будет 20-й день. Ответ: за 19 дней. Задача 2: Мама послала Алешу в магазин за покупками, вручив ему кошелек с деньгами. Половину денег Алеша уплатил за молоко и сыр. Доехав за 3 р. на автобусе до магазина, половину оставшихся денег и еще 1 р. он уплатил за книгу. На половину того, что еще осталось, Алеша купил тетрадей. Выйдя из магазина, он купил мороженое за 4 р., оставив деньги лишь на обратный проезд на автобусе. Сколько денег мама дала Алеше? Решение: Так как нам известно количество денег перед последней покупкой, то задачу проще решать с конца. После покупки тетрадей у Алеши осталось 7 р., значит, за тетради он заплатил 7 р. Тогда 14 р. вместе с 1 р. – это половина денег, бывших у Алеши до покупки книги. Тогда до покупки книги у него было 30 р. Поэтому после покупки молока и сыра у Алеши оставалось 33 р., а это половина первоначальной суммы. Т.е. мама дала Алеше 66 р. Задача 3: 48 спичек разложены по трем кучкам. Известно, что если из первой кучки переложить во вторую столько спичек, сколько в этой второй кучке имеется, а затем из этой второй переложить в третью столько, сколько в этой третьей находится и, наконец, из третьей переложить в первую столько спичек, сколько в этой первой кучке будет тогда находиться, то число спичек во всех кучках станет одинаковым. Сколько спичек было в каждой кучке первоначально? Решение: Эту задачу также проще решать с конца. Так как после всех перекладываний число спичек в кучках стало одинаковым, то в каждой кучке их оказалось 48:3 = 16 штук. Перед этим в первой кучку добавили столько спичек, сколько в ней было, т.е. 8 штук. Эти 8 спичек взяли из третьей кучки, т.е. там перед последним перекладыванием было 16 + 8 = 24 спички. Но эти 24 спички мы получаем перекладыванием из второй кучки в третью такого количества спичек, какое в третьей кучке уже было. Т.е. удвоением спичек. Значит до второго перекладывания в третьей кучке было 12 спичек, а во второй 16 + 12 = 28 спичек. Рассуждая аналогично получаем, что во второй кучке 14 спичек, а в первой 8 + 14 = 22 спички. Ответ: Первоначально в первой кучке было 22 спички, во второй – 14, а в третьей – 12. Задача 4: Алеша задумал число. Он прибавил к нему 5, потом разделил сумму на 3, умножил на 4, отнял 6, разделил на 7 и получил число 2. Какое число задумал Алеша? Решение: 10 Задача 5: Микрокалькулятор позволяет делать с введённым в него числом две операции: умножать на 2 или переставлять его цифры. Можно ли получить из числа 1 число 68? Задача 6: В колбу пустили бактерию. Каждую минуту число бактерий удваивается. Через три часа колба заполнилась бактериями. В какой момент бактериями была заполнена четверть колбы? Решение: Через 2 часа 58 минут. Задача 7: Над озерами летели гуси. На каждом садилась половина гусей и еще полгуся, остальные летели дальше. Все сели на 7 озерах. Сколько было гусей? Решение: 127. Задача 8: Клетчатая доска 8 × 8 выложена плитками домино 1 × 2. Докажите, что какие-то две из них образуют квадрат из четырёх клеток. Задача 9: Учитель раздавал школьникам открытки. Первому он дал одну открытку и одну десятую оставшихся. Второму он дал две открытки и одну десятую оставшихся и т.д. Девятому он дал девять открыток и одну десятую оставшихся. Оказалось, что все получили поровну и все открытки были розданы. Сколько всего было открыток? Решение: 81 Задача 10: По кругу расставлены 9 нулей и единиц, причём не все они равны. За один ход между каждыми двумя соседними числами записывается 0, в случае если они равны, и 1 в противном случае. Далее старые числа стираются. Могут ли в конце все числа оказаться равными? Решение: Нет, не могут Задача 11: За столом сидят 7 гномов, перед каждым – кружка, в некоторые налит эль (но, быть может, не поровну). Первый разлил весь свой эль поровну в кружки всем остальным. Затем второй разлил свой эль поровну всем остальным (включая первого), затем третий гном и т.д. до седьмого. Когда и седьмой гном разлил свой эль, у всех оказалось столько же эля, сколько было вначале. Сколько эля в каждой кружке, если всего его 3 литра? Решение: 6/7, 5/7, 4/7, 3/7, 2/7, 1/7 и 0. Задача 12: На большой клетчатой доске стоят (живут) несколько шашек. За один ход некоторые шашки убираются с доски (умирают), кроме того на некоторых клетках шашки появляются (рождаются). Рождение и смерть происходят одновременно на всех клетках по следующим законам: Живая шашка умирает, если у неё меньше двух или больше трёх живых соседей (по стороне или углу). Шашка рождается в клетке, если у этой клетки три соседа (по стороне или углу). Оказалось, что на доске шашки стоят так, как показано на рисунке. Какое положение шашек могло быть за ход до этого?  |
