Задачи. Олимпиадные задачи по математике за 6 класс - Погребникова Алена. Арифметика На карточках записаны цифры 1, 2, Из этих карточек составлены числа и записано неверное равенство. Покажите, как, переместив только одну карточку, сделать равенство верным. 1
 Скачать 0.53 Mb.
|
Олимпиадные задания по математике с решениями.6-8 классы.
Ответы:
6 класс 1. Кассир продал все билеты в первый ряд кинотеатра, причем по ошибке на одно из мест было продано два билета. Сумма номеров мест на всех этих билетах равна 857. На какое место продано два билета? 2. Каждый из трёх приятелей либо всегда говорит правду, либо всегда лжёт. Им был задан вопрос: «Есть ли хотя бы один лжец среди двух остальных?» Первый ответил: «Нет», второй ответил: «Да». Что ответил третий?  3. Существует ли 10-угольник, который можно разрезать на 5 треугольников? 4. Вася и Митя играют в «морской бой» на поле размером 8 8 по следующим правилам. Митя расставляет 16 одноклеточных кораблей так, чтобы они не соприкасались (даже углами). Каждым ходом Вася называет одну из клеток поля и, если на этой клетке стоит корабль, то корабль считается уничтоженным. Докажите, что независимо от расстановки кораблей Вася за 4 хода сможет уничтожить хотя бы один корабль. 5. На острове Невезения отменили понедельники: у них за воскресеньем сразу следует вторник. За последний год (то есть, с 15 декабря 2009 года по 14 декабря 2010 года) воскресенья на острове совпадали с нашими воскресеньями ровно восемь раз. Какой день недели на острове сегодня? 6. На каждом километре между селами Марьино и Рощино стоит столб с табличкой, на одной стороне которой написано расстояние до Марьино, на другой – расстояние до Рощино. Останавливаясь у каждого столба, Бобик заметил, что если сложить все цифры, записанные на обеих сторонах таблички, то получится 13. Найдите расстояние между селами. 7. По кругу стоят восемь козлов разного роста. Любой из них умеет перепрыгивать через двух соседних козлов против часовой стрелки. Докажите, что при любом начальном расположении козлов они смогут встать по росту. Решения и ответы 1. Кассир продал все билеты в первый ряд кинотеатра, причем по ошибке на одно из мест было продано два билета. Сумма номеров мест на всех этих билетах равна 857. На какое место продано два билета? Ответ: на тридцать седьмое место. Выясним, сколько мест могло быть в первом ряду. Во-первых, их не больше 40, так как сумма натуральных чисел от 1 до 41 равна 861. Во-вторых, их не меньше 40, так как сумма натуральных чисел от 1 до 39 равна 780, и даже после прибавления к ней 39, результат будет меньше 857. Значит в первом ряду ровно 40 мест. Теперь несложно определить, на какое место был продан лишний билет: 1 + … + 40 = 820; 857 – 820 = 37. 2. Каждый из трёх приятелей либо всегда говорит правду, либо всегда лжёт. Им был задан вопрос: «Есть ли хотя бы один лжец среди двух остальных?» Первый ответил: «Нет», второй ответил: «Да». Что ответил третий? Ответ: «Нет». Заметим, что так как первый и второй приятели дали различные ответы, то один из них – лжец, а другой – рыцарь. Кроме того, рыцарь не мог ответить «Нет» на предложенный ему вопрос, так как в этом случае он бы сказал неправду (среди двух оставшихся точно есть лжец). Следовательно, первый – лжец. Он солгал, значит среди двух оставшихся должен быть лжец, и им может быть только третий приятель. Значит третий ответил «Нет». 3. Существует ли 10-угольник, который можно разрезать на 5 треугольников? 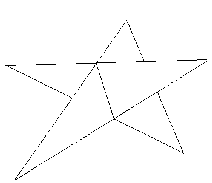 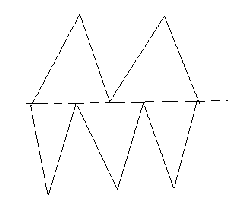 Ответ: существует. Например, см. рисунки. 4. Вася и Митя играют в «морской бой» на поле размером 88 по следующим правилам. Митя расставляет 16 одноклеточных кораблей так, чтобы они не соприкасались (даже углами). Каждым ходом Вася называет одну из клеток поля и, если на этой клетке стоит корабль, то корабль считается уничтоженным. Докажите, что независимо от расстановки кораблей Вася за 4 хода сможет уничтожить хотя бы один корабль. Разрежем поле для игры на 16 квадратов размером 22. Заметим, что в каждом таком квадрате не может стоять более одного корабля (иначе корабли будут соприкасаться). Так как всего кораблей 16, то в каждом квадрате должен стоять корабль. Таким образом, Васе достаточно полностью «расстрелять» один из этих квадратов. 5. На острове Невезения отменили понедельники: у них за воскресеньем сразу следует вторник. За последний год (то есть, с 15 декабря 2002 года по 14 декабря 2003 года) воскресенья на острове совпадали с нашими воскресеньями ровно восемь раз. Какой день недели на острове сегодня? Ответ: суббота. Так как обычная неделя состоит из семи дней, а неделя на острове – из шести, то совпадение воскресений происходит один раз в 67 = 42 дня. Значит, за 378 дней происходит 9 совпадений. Поскольку 378 – 365 = 13, то девятое совпадение должно произойти в течение ближайших тринадцати дней (с 15 по 27 декабря). Единственное воскресенье в этот период – 21 декабря. Непосредственным подсчетом получаем, что сегодня на острове – суббота. 6. На каждом километре между селами Марьино и Рощино стоит столб с табличкой, на одной стороне которой написано расстояние до Марьино, на другой – расстояние до Рощино. Останавливаясь у каждого столба, Бобик заметил, что если сложить все цифры, записанные на обеих сторонах таблички, то получится 13. Найдите расстояние между селами. Ответ: 49 километров. Расстояние между селами не может быть больше, чем 49 километров, так как тогда на одном из столбов будет написано с одной стороны 49, а с другой – не 0, то есть, сумма цифр будет больше 13. На первых девяти столбах с одной стороны записаны однозначные числа от 1 до 9, поэтому числа, записанные с другой стороны, также должны быть из одного десятка (чтобы суммы цифр были одинаковы). Следовательно, искомое расстояние выражается числом, оканчивающимся на 9. Числа 9, 19, 29 и 39 решениями не являются, так как на первом столбе сумма цифр не будет равна 13. Таким образом, искомое расстояние равно 49 километрам.  7. По кругу стоят восемь козлов разного роста. Любой из них умеет перепрыгивать через двух соседних козлов против часовой стрелки. Докажите, что при любом начальном расположении козлов они смогут встать по росту. На рисунке показано, каким образом любой козел (черный) сможет допрыгать до любого места, то есть, встать за любым (белым), заранее выбранным. В это время остальные козлы стоят на своих местах. Поэтому, сначала второй по росту козел встанет за самым высоким, после чего за ним встанет следующий по росту, и так далее. Такая операция возможна потому, что числа 2 и 7 – взаимно простые. Основной тур Даны две палочки. Их можно прикладывать друг к другу и делать отметки. Как с помощью этих операций выяснить, что больше – длина более короткой палочки, или 2/3 длины более длинной палочки? Одно число увеличили на 2%, а другое на 3%. Могла ли сумма увеличиться на 5%? (Числа считаются положительными.) С  колькими способами можно разрезать доску, показанную на рисунке, на прямоугольники из двух клеток так, чтобы в каждой части была закрашенная клетка?П  етя выкладывал примеры из спичек. Цифры он «записывал» следующим образом: К  огда Петя отвлёкся, Вася в записанном им верном примере на сложение внутри каждой цифры переложил ровно одну спичку и получил: Восстановите исходное равенство. Дополнительный тур В 6А классе учится 27 школьников. Им предложили посещать кружки по пению, молчанию и чтению стихов. Каждый хочет посещать один или несколько из этих кружков. Оказалось, что в каждый кружок желает ходить более трети класса. Можно ли составить такие списки кружков, что каждый будет ходить ровно в один кружок, в который хочет, и во всех кружках будет поровну школьников? Четыре друга участвовали в олимпиаде. Витя решил больше всех задач – восемь, а Петя меньше всех – пять задач. Каждая задача олимпиады была решена ровно тремя из друзей. Сколько задач было на олимпиаде? К  летки тетрадного листа раскрашены в восемь цветов. Докажите, что найдется фигура вида, указанного на рисунке, внутри которой есть клетки одного цвета.Олимпиадные задачи по математике 6 класса решите уравнение: 0,5  Найдите все дроби со знаменателем 15, которые больше  и меньше 1.Возраст старика Хоттабыча записывается числом с различными цифрами. Об этом числе известно следующее: Если первую и последнюю цифру зачеркнуть, то получится двузначное число, которое при сумме цифр, равной 13, является наибольшим; Первая цифра больше последней в 4 раза. Сколько лет Хоттабычу? Некоторый товар стоил 500 рублей. Затем цену товара увеличили на 10%, а затем уменьшили на 10%. Какой стала цена товара в итоге? В летний лагерь приехали отдыхать три друга: Миша, Володя и Петя. Известно, что каждый из них имеет одну из следующих фамилий: Иванов, Семенов, Герасимов. Миша – не Герасимов. Отец Володи – инженер. Володя учится в 6 классе. Герасимов учится в 5 классе. Отец Иванова – учитель. Какая фамилия у каждого из трех друзей? Решения. x = 5. Числа и 1 представим в виде дроби со знаменателем, кратным 15. Тогда  ; 1= . Между числами и 1 лежат дроби  Условию удовлетворяет лишь  Так как после зачеркивания получается наибольшее число с суммой цифр 13, то вторая и третья цифры равны 9 и 4. Так как первая цифра больше последней в 4 раза и все цифры различны, то первая цифра будет 8, а последняя 2. В результате получаем число 8942. Старику Хоттабычу 8942 года. 550-55 = 495 (руб.) – стала цена в итоге. Так как Володя учится в 6 классе, а Герасимов в 5 классе, то Володя не Герасимов. Так как отец Иванова – учитель, отец Володи – инженер, то Володя – не Иванов. Тогда Володя - Семенов, Миша – Иванов, а Петя – Герасимов |