Задачи. Олимпиадные задачи по математике за 6 класс - Погребникова Алена. Арифметика На карточках записаны цифры 1, 2, Из этих карточек составлены числа и записано неверное равенство. Покажите, как, переместив только одну карточку, сделать равенство верным. 1
 Скачать 0.53 Mb. Скачать 0.53 Mb.
|
|
6. Логическая задача. 1) на движение 1. Могут ли три человека преодолеть расстояние в 60 км за 3 часа, если у них в распоряжении имеется двухместный мотоцикл? Скорость мотоцикла 50 км/ч, скорость пешехода 5 км/ч. Решение. 1 час : Два человека (А и В) едут на мотоцикле и проезжают 50 км, а третий человек (С) идёт пешком и проходит 5 км. 2 час: Человек (В) сходит с мотоцикла и идёт пешком. Он проходит 5 км. Человек (С) идёт пешком и проходит ещё 5 км. Человек (А) возвращается на 40 км и ждёт человека (С) там. 3 час: Два человека (А и С) на мотоцикле добираются до пункта назначения. Человек (В) проходит ещё 5 км и оказывается в пункте назначения. Ответ. Могут 2. Мотоциклист, велосипедист и пешеход движутся по шоссе в одну сторону с постоянными скоростями. Когда велосипедист поравнялся с пешеходом, мотоциклист отставал от них на 6 км. Когда мотоциклист догнал велосипедиста, пешеход отстал от них на 3 км. Какое было расстояние между пешеходом и велосипедистом, когда мотоциклист догнал пешехода? Решение. Изобразим упомянутые в условии ситуации: 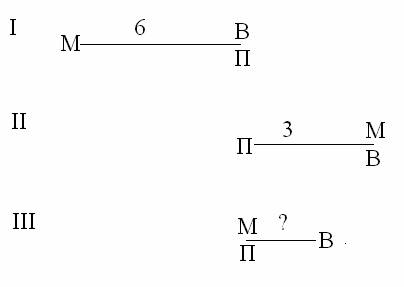 Сразу видно, что третье расположение следовало первому и предшествовало второму. Рассмотрим движение мотоциклиста и велосипедиста относительно пешехода. Сколько километров относительно пешехода проехал мотоциклист от первой до второй ситуации? 3+6=9 километров Сколько километров относительно пешехода проехал велосипедист от первой до второй ситуации? 3 километра. Во сколько раз скорость мотоциклиста относительно пешехода больше скорости велосипедиста относительно пешехода? 9/3=3 раза. Сколько километров относительно пешехода проехал мотоциклист между первой и третьей ситуациями? 6 километров Сколько километров относительно пешехода за это же время проедет велосипедист? Т.к. его относительная скорость втрое меньше, то 6/3=2 километра. Ответ: 2 километра 2) на взвешивание 1. Из девяти монет одна фальшивая: она легче остальных. Как за два взвешивания на чашечных весах без гирь определить, какая именно? Решение. Разобьём монеты на 3 кучки по 3 монеты и проведём взвешивания. Первое взвешивание: положим по 3 монеты на каждую чашку весов. Возможны два случая: 1. Равновесие, тогда на весах только настоящие монеты, а фальшивая среди тех монет, которые не взвешивались. 2. Одна из кучек легче, то в ней фальшивая монета. Второе взвешивание: теперь требуется найти фальшивую среди трёх монет( по методу первого взвешивания). 2. Известно, что монеты: 1к., 2к., 3к. и 5 к. весят, соответственно, 1, 2, 3 и 5 граммов. Среди четырёх монет (по одной каждого достоинства) одна фальшивая. Она отличается весом от настоящей. Как с помощью взвешиваний на чашечных весах без гирь определить фальшивую монету? Решение. Чтобы узнать какая монета фальшивая выполним следующие взвешивания:
Если при первом взвешивании будет равновесие, то бракованная монета – 5 к. Если при втором, то бракованная монета – 1 к. Если же равновесия не будет, то обе монеты, 1 к. и 5 к., - настоящие, а одна из монет, 2 коп или 3 коп, - бракованная. Кроме того, из второго взвешивания можно будет сделать вывод легче или тяжелее настоящей фальшивая монета. Если при первом взвешивании перевесит та же чашка весов, что и при втором, то фальшивая монета – 2 к., иначе 3к. 3. Имеется 10 мешков монет. В 9 мешках монеты настоящие (весят по 10г), а в одном фальшивые (весят по 11 г) Одним взвешиванием на электронных весах определить, в каком мешке фальшивые монеты? Решение. Занумеруем мешки и возьмем из каждого мешка количество монет, соответствующее его номеру ( из первого мешка 1 монету, из второго –2…)Всего мы возьмем 1+2+3+…+10=55 монет. Если бы все они были настоящие, то их общая масса составила 550г, но среди них есть и фальшивые, поэтому эта масса будет больше. Если фальшивые монеты в 1 ящике, то разница в массе составит 1 г., а если во втором- 2 г. и т.д. Определив эту разницу, мы и узнаем в каком мешке фальшивые монеты. 3) на принцип Дирихле 1. Пятнадцать мальчиков собрали вместе 100 орехов. Докажите, что какие-то двое из них собрали одинаковое количество орехов. Решение: Предположим противное – тогда мальчики собрали не меньше, чем 0 + 1 + 2 + … + 14 = 105 орехов. Противоречие. 2. Верно ли, что среди любых 34 разных натуральных чисел, не превосходящих 50, всегда можно выбрать два числа, одно из которых вдвое больше другого? Решение: Да, верно. Разобьем числа на такие пары-клетки: (1,2), (3,6), (5,10), …, (25,50); (4,8), (12,24), (20,40); (16,32). Добавим к этим 17-ти парам ещё не использованные 16 чисел, не превосходящих 50 (27, 28, 29, 31, 33, 35, 36, 37, 39, 41, 43, 44, 45, 47, 48, 49), каждое из них образует отдельную клетку. Всего получилось 33 клетки, поэтому в одну из них попадут хотя бы два данных числа. В «одноместную» клетку они попасть не могут, значит, они попали в пару, так что одно из них действительно в два раза больше другого. 3. В магазин привезли 25 ящиков с тремя разными сортами яблок (в каждом ящике яблоки только одного сорта). Докажите, что среди них есть по крайней мере 9 ящиков с яблоками одного и того же сорта. Решение: Предположим, что ящиков с конфетами каждого из трёх сортов привезли не более восьми, тогда всего привезли бы 8 · 3 = 24 ящика. Это противоречит условию задачи. Значит, найдутся 9 ящиков с одинаковым сортом конфет. 4. 10 школьников на олимпиаде решили 35 задач, причем известно, что среди них есть школьники, решившие ровно одну задачу, школьники, решившие ровно две задачи и школьники, решившие ровно три задачи. Докажите, что есть школьник, решивший не менее пяти задач. Решение: Из условий следует, что найдутся 7 школьников, решивших 35 – 6 = 29 задач. Так как 29 = 4 • 7 + 1, то найдется школьник, решивший не менее пяти задач. 5. Пятеро молодых рабочих получили на всех зарплату – 1500 рублей. Каждый из них хочет купить себе магнитофон ценой 320 рублей. Докажите, что кому-то из них придется подождать с покупкой до следующей зарплаты. Решение: Если бы каждый из рабочих мог купить магнитофон, то у них в сумме было бы не менее 5 • 320 = 1600 рублей. 6. Сто человек сидят за круглым столом, причем более половины из них – мужчины. Докажите, что какие-то два мужчины сидят друг напротив друга. Решение: Разобьем всех людей на 50 пар так, что в каждой паре – два человека, сидящих друг напротив друга. Ясно, что в одной из этих пар-«клеток» оба человека – мужчины. 7. В городе 15 школ. В них обучается 6015 школьников. В концертном зале городского дворца культуры 400 мест. Доказать, что найдётся школа, ученики которой не поместятся в этот зал. Решение: Предположим, что в каждой школе не более 400 учеников. Значит, в 15 школах не более 15 · 400 = 6000 школьников. Но по условию в школах обучаются 6015 человек. Значит, найдется школа, в которой больше 400 учеников. Поэтому ученики этой школы не поместятся в зал на 400 мест. 4) на взаимно однозначное соответствие 1. В кругу стоят девочки: Ася, Катя, Галя и Нина, одетые в зелёное, голубое, белое, розовое платья. Девочка в зелёном платье (не Ася и не Катя) стоит между девочкой в голубом платье и Ниной. Девочка в белом платье стоит между девочкой в розовом платье и Катей. Какого цвета платье было надето на каждой из девочек?
Ответ: Галя – в зелёном, Катя – в голубом, Ася – в белом, Нина – в розовом. 2. Учащиеся школы решили организовать инструментальный ансамбль. Михаил играет на саксофоне. Пианист учится в 9 классе. Ударника зовут не Валерием, а ученика 10 класса зовут не Леонидом. Михаил учится не в 11 классе. Андрей – не пианист и не ученик 8 класса. Валерий учится не в 9 классе, ударник - не в 11. Леонид играет не на контрабасе. На каком инструменте играет Валерий и в каком классе он учится? Решение.
Валерий играет на контрабасе. Для того, чтобы определить в каком он классе составим ещё одну таблицу.
Ответ. Валерий играет на контрабасе и учится в 11 классе. 3. В семье 4 ребенка. Младшему 5, старшему 15 лет. Двум другим 8 и 13 лет. Имена детей: Боря, Галя, Вера и Аня. Какой возраст каждого ребенка, если одна девочка ходит в детский сад. Аня старше Бори. Сумма лет Ани и Веры делится на 3.
Ответ: Аня 13, Боря 8, Вера 5, Галя 15 4. Царь призвал ко двору трех богатырей. И спрашивает: - Кто убил Змея Горыныча? Илья Муромец сказал: — Змея убил Добрыня Никитич. Добрыня Никитич сказал: — Змея убил Алёша Попович. Алёша Попович сказал: — Я убил змея. Только один богатырь сказал правду, остальные два слукавили. Так кто же убил Змея Горыныча? Решение. Допустим, Илья слукавил, тогда Змея убил, например, Алеша. Тогда двое других богатырей сказали правду, но это противоречит условию. Тогда пусть сам Илья и убил, а сказал неправду из скромности. Тогда и другие богатыри соврали. Значит правду сказал Илья Муромец: Змея убил Добрыня Никитич. 5. Михаилу в викторине предложили выбрать один из ящиков. В одном из ящиков спрятан приз. Михаил получил 4 подсказки - приз в желтом или красном ящике - приз в зеленом или синем ящике - приз в зеленом ящике - в желтом ящике приза нет Три подсказки ошибочны, но только одна правильная. Андрей подумал и открыл правильный ящик. Какого цвета? Ответ: Желтый 5) на круги Эйлера 1. На спортивные соревнования в ЛМШ ходили 220 школьников. При этом некоторые из них участвовали в чемпионатах, а остальные были зрителями. В легкоатлетической эстафете приняли участие 30 человек, в соревнованиях по волейболу – 26, пионерболу – 32, футболу – 31, шахматам – 28 и теннису – 36 человек. 53 школьника приняли участие более чем в одном соревновании; из них 24 школьника участвовали 3 или более раз, 9 школьников – не менее 4 раз и 3 школьника – даже 5 раз (в последнюю тройку входит и один чудак, который выступал во всех шести соревнованиях). Сколько из школьников были зрителями? Решение: В сумме в них были 30 + 26 + 32 + 31 + 28 + 36 = 183 школьника. Число школьников, игравших хотя бы один раз, равно 183 – 53 – 24 – 9 – 3 – 1 = 93. Оставшиеся 127 школьников были зрителями. 2. Из 100 туристов, отправляющихся в заграничное путешествие, немецким языком владеют 30 человек, английским – 28, французским – 42. Английским и немецким одновременно владеют 8 человек, английским и французским – 10, немецким и французским – 5, всеми тремя языками – 3. Сколько туристов не владеют ни одним языком? Решение: только английским владеет 13 человек, только французским – 30, только немецким – 20 человек. 20 человек не знают ни одного из этих языков. 6) комбинаторные задачи 1. Сколькими способами победитель «Поля чудес» может выбрать два приза из 50 имеющихся? Решение: (50 × 49)/2=1225. 2. Сколькими способами можно из 50 участников собрания выбрать председателя и секретаря? Решение: 50 × 49=2450. 3. Сколькими способами можно зажечь свет в нашем классе? (в классе 3 лампочки, у каждой – отдельный выключатель) | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
