|
|
арккосинус. Арккосинус числа а. Решение уравнений cos x a
Тема урока: Арккосинус числа а. Решение уравнений cos x = a.
Тип урока: изучение нового материала
Цели урока:ввести понятие арккосинуса числа а; выработать навык вычисления арксинуса числа а; вывести формулу корней простейших тригонометрических уравнений формулу cos x = a;
Предметные: умение применять формулу при решении простейших тригонометрических уравнений;
Личностные: развивать умение кратко, логично, последовательно излагать мысли и суждения; развивать способность аргументировать свои утверждения; развивать умения классифицировать, сравнивать, анализировать и делать выводы.
Коммуникативные: умение вступать в диалог с одноклассниками и учителем
Регулятивные: обучать навыкам планирования деятельности, работы в оптимальном темпе, воспитывать умение правильно оценивать свои возможности, результаты учебной деятельности, развивать коммуникативные навыки;
Познавательные: воспитывать трудолюбие и целеустремленность.
Ход урока:
Организационный момент
2.Актуализация знаний
Вычислить значения: cos 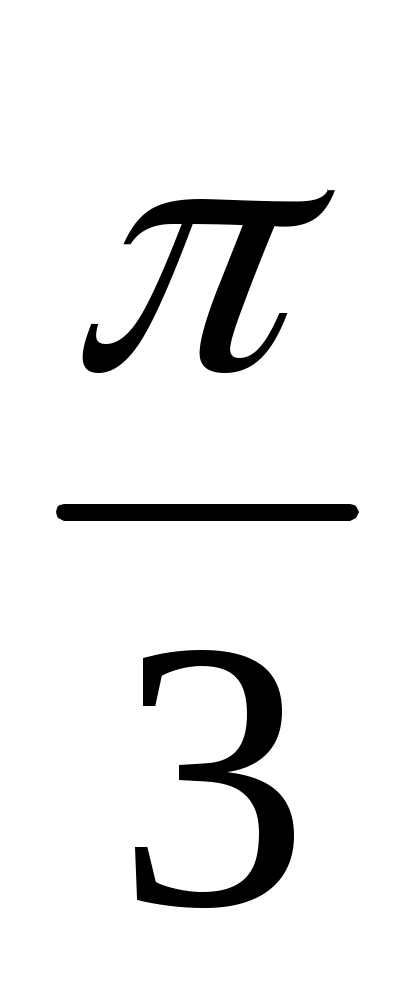 ; cos ; cos 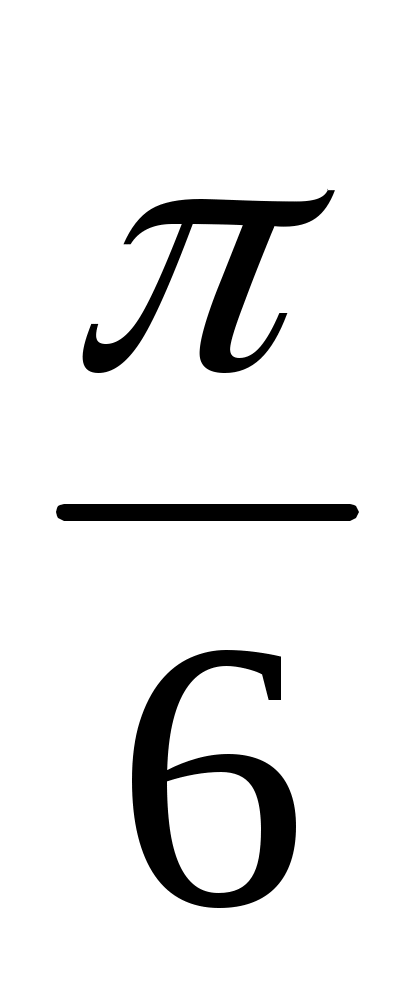 ; cos ; cos 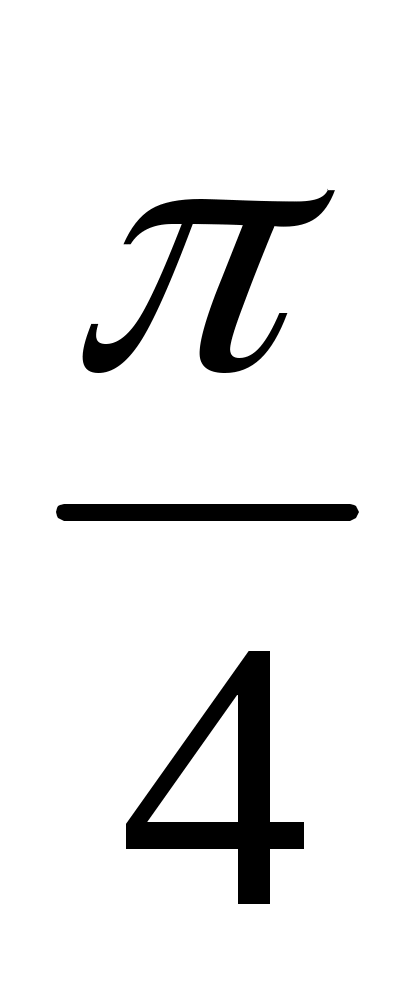 . .
Учитель
|
Ученик
|
Точки единичной окружности 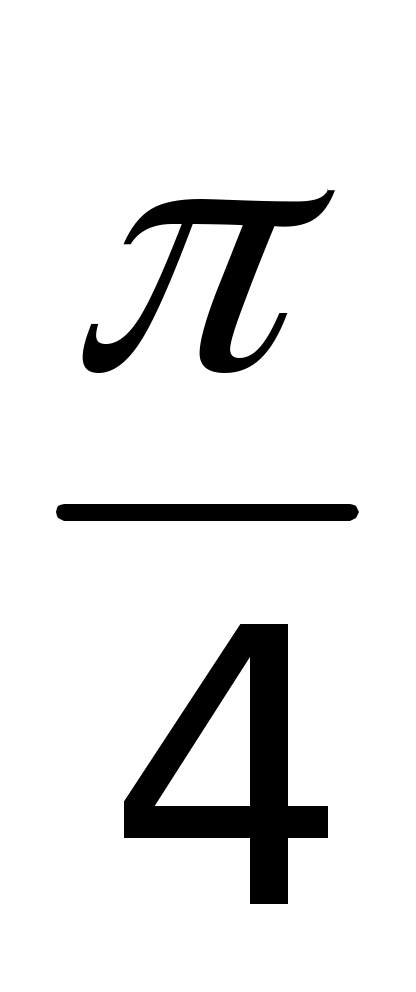 , ,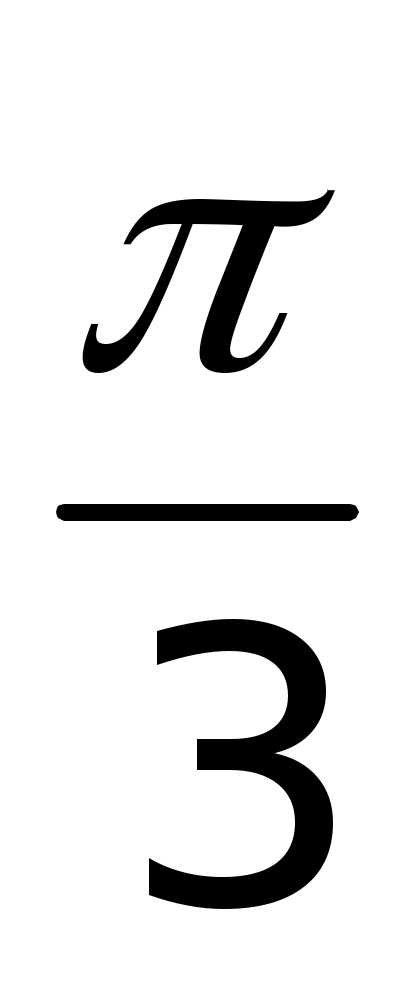 , ,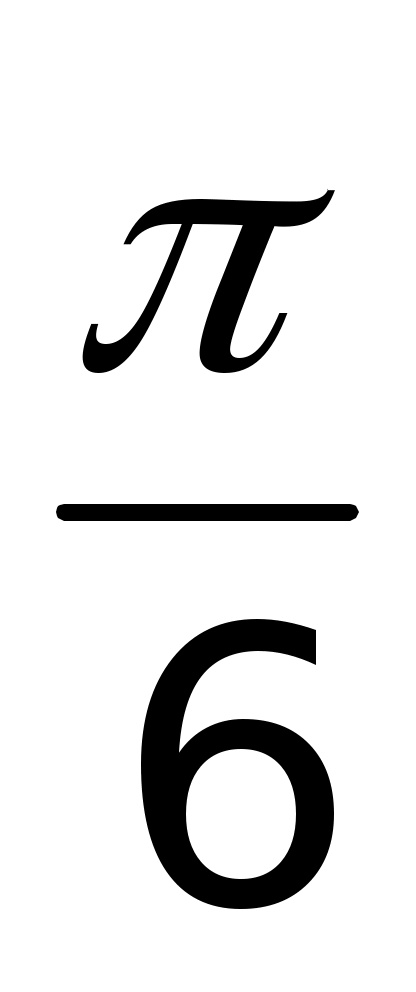 принадлежат какой четверти? принадлежат какой четверти?
|
Точки единичной окружности 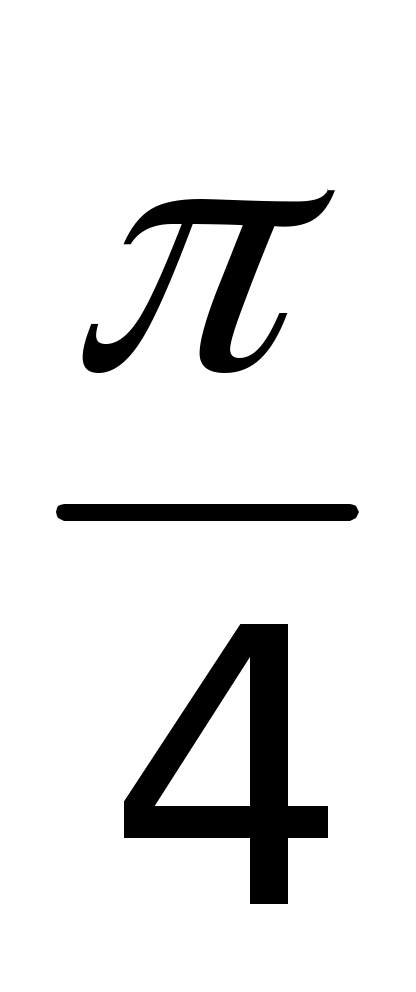 , ,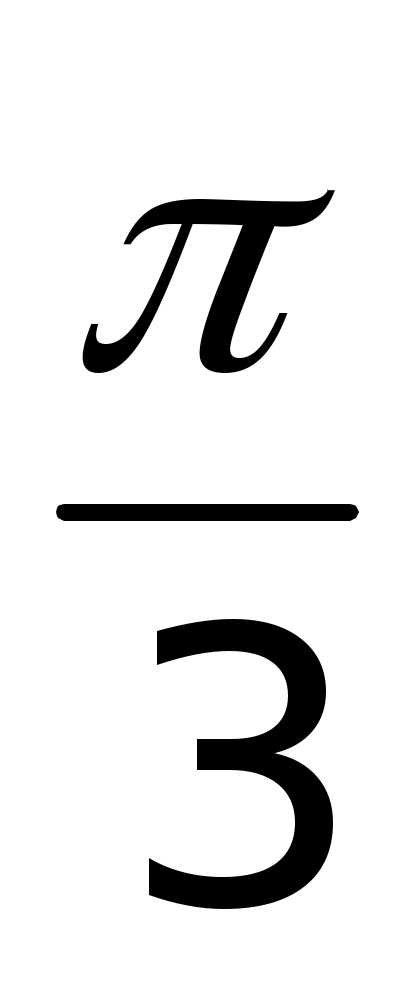 , ,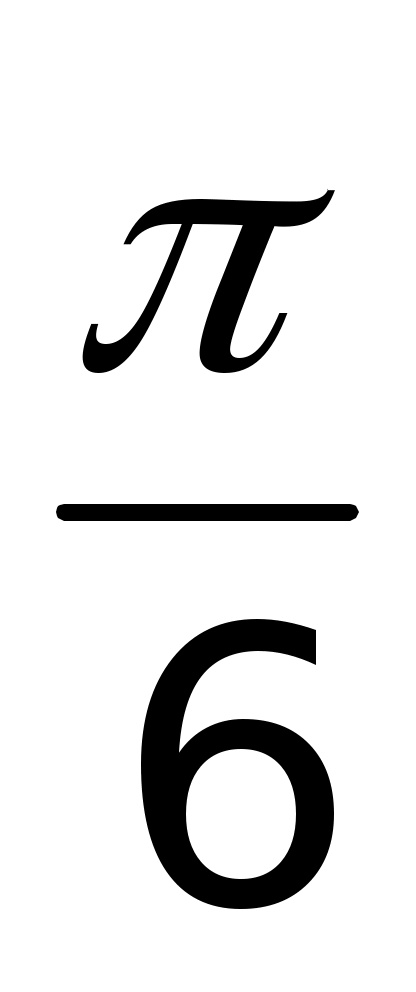 принадлежат 1четверти? принадлежат 1четверти?
|
Косинус какого угла есть величина положительная?
Вывод: Косинус острого угла есть величина положительная.
|
- Если угол принадлежит 1 четверти
|
2. Вычислить значения: cos 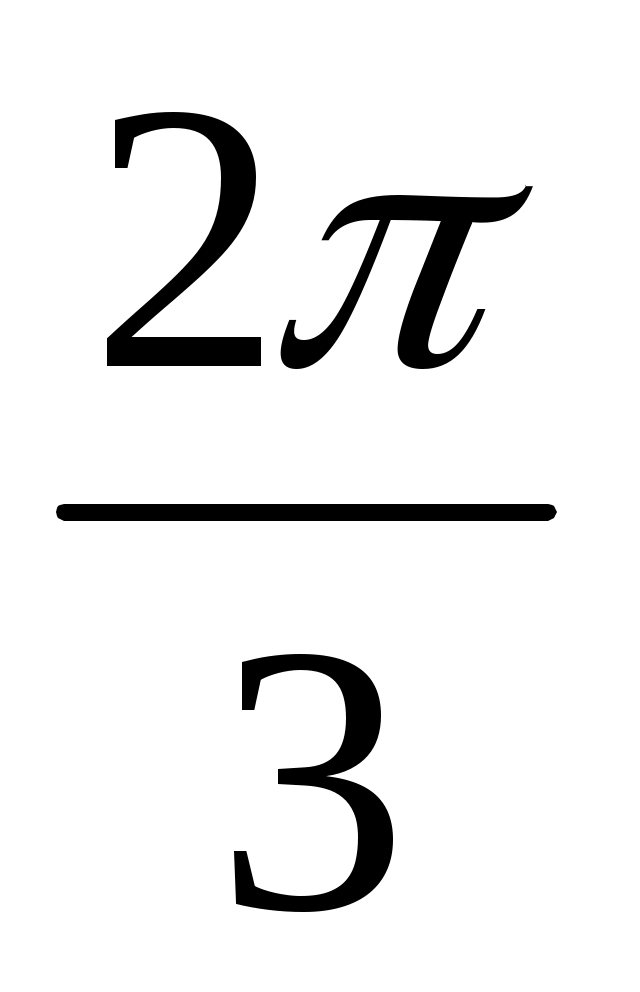 ; cos ; cos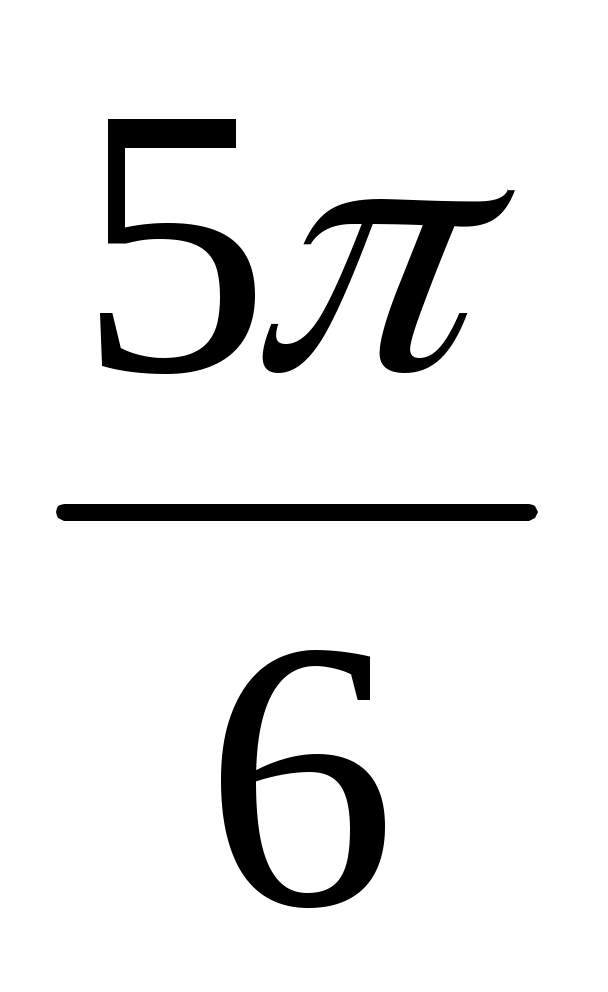 ; cos ; cos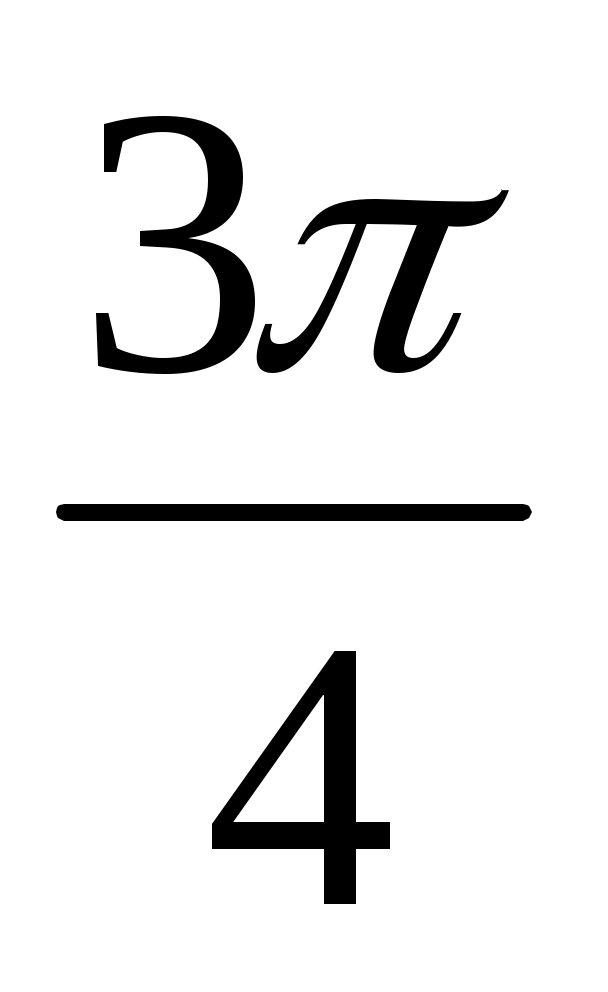
Учитель
|
Ученик
|
Точки единичной окружности 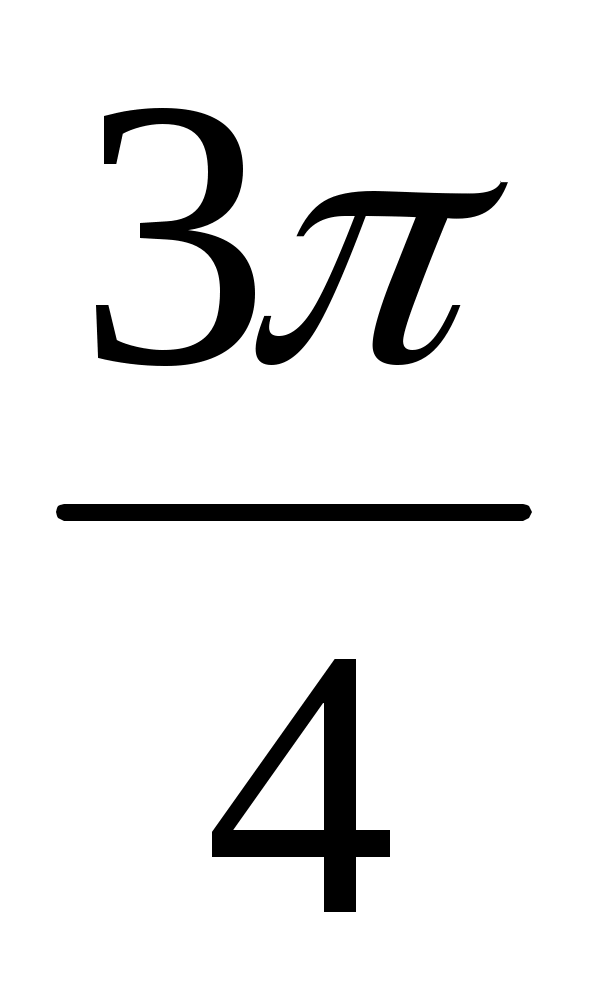 , ,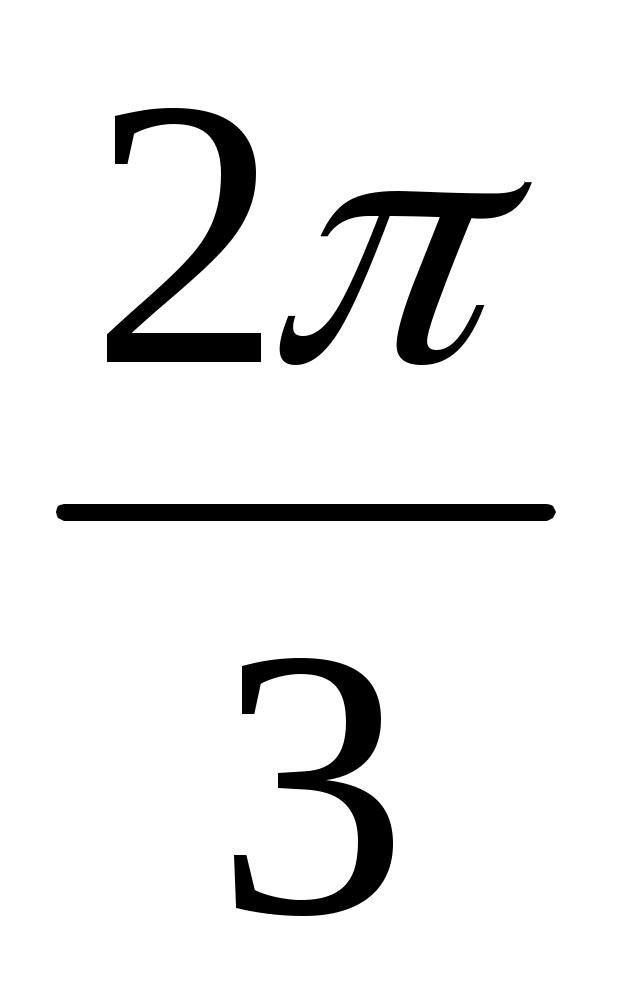 , ,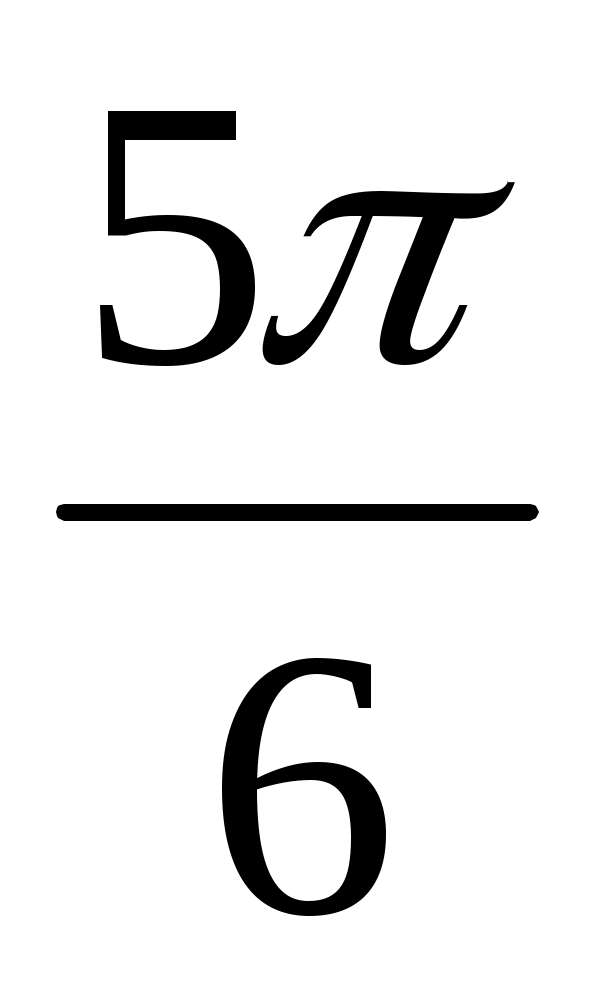 принадлежат какой четверти? принадлежат какой четверти?
|
Точки единичной окружности 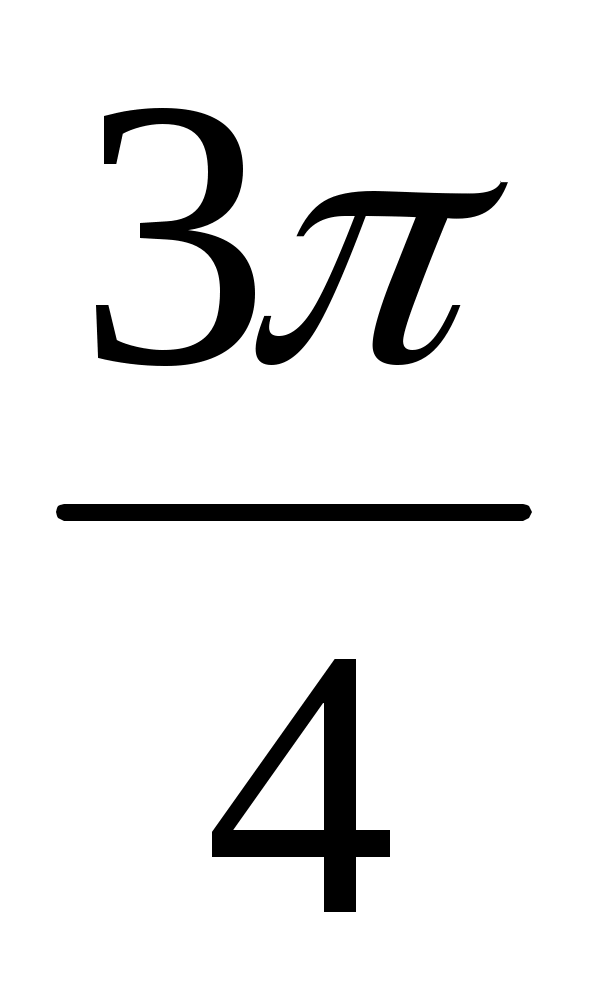 , ,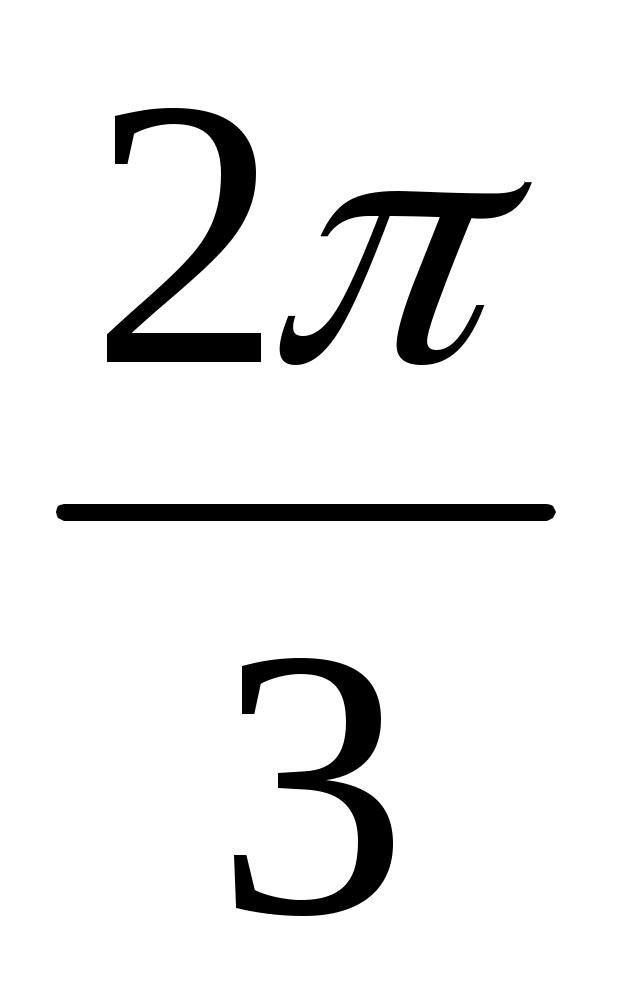 , ,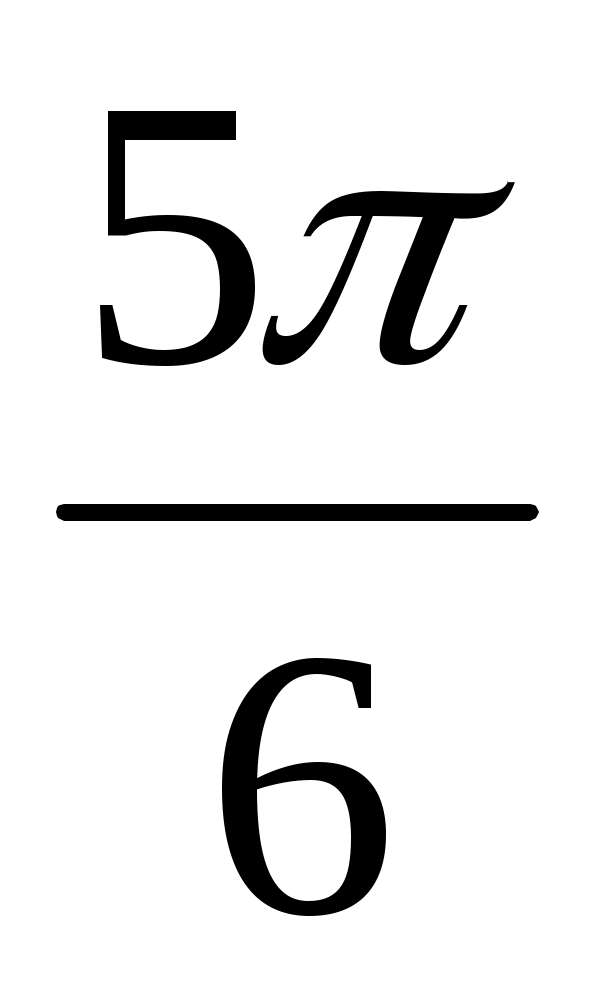 принадлежат 2 четверти. принадлежат 2 четверти.
|
Косинус какого угла есть величина отрицательная?
Вывод: Косинус тупого угла величина отрицательная
|
- Если угол принадлежит 2 четверти
|
3.Косинус какого угла равен 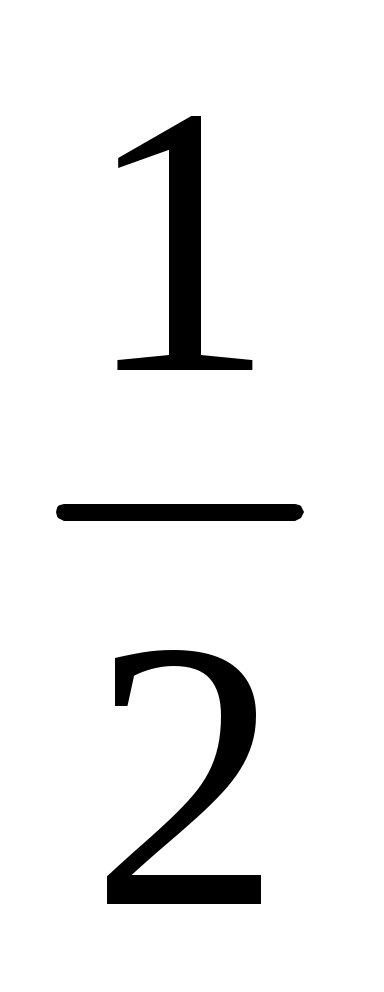 ; 0; ; 0; 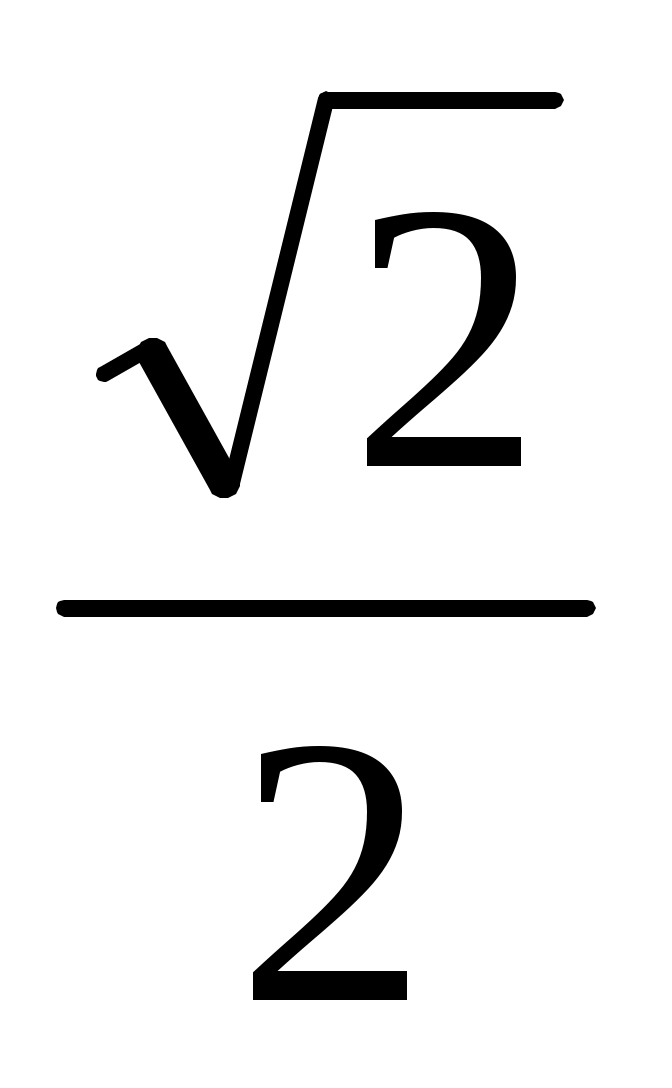 ; 1; ; 1; 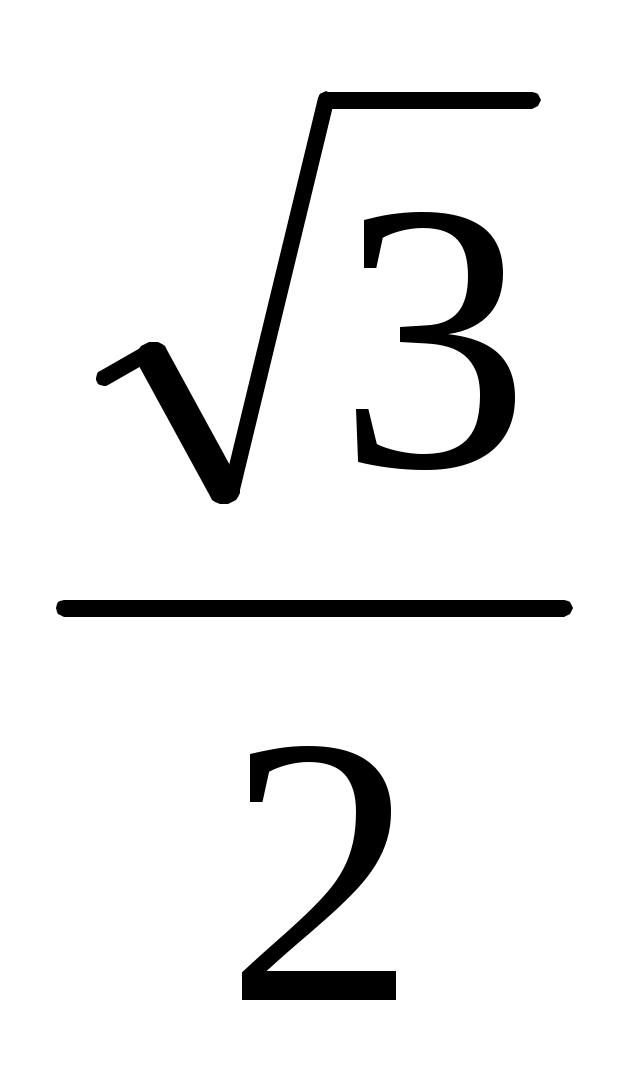 ; - ; -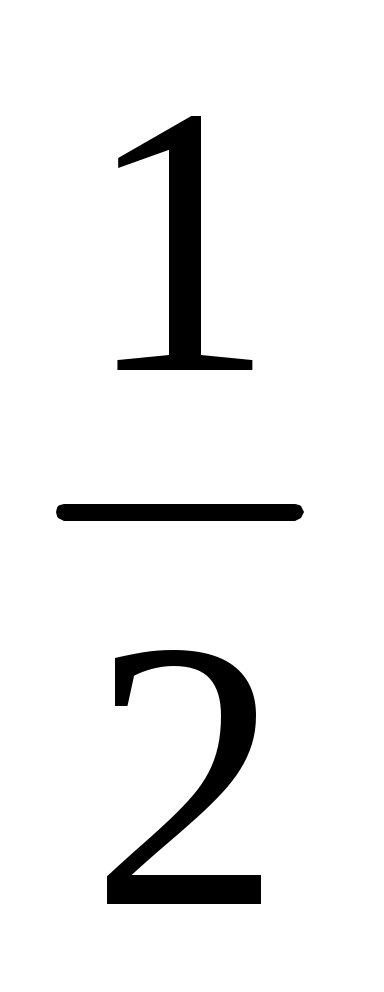 ; - ; -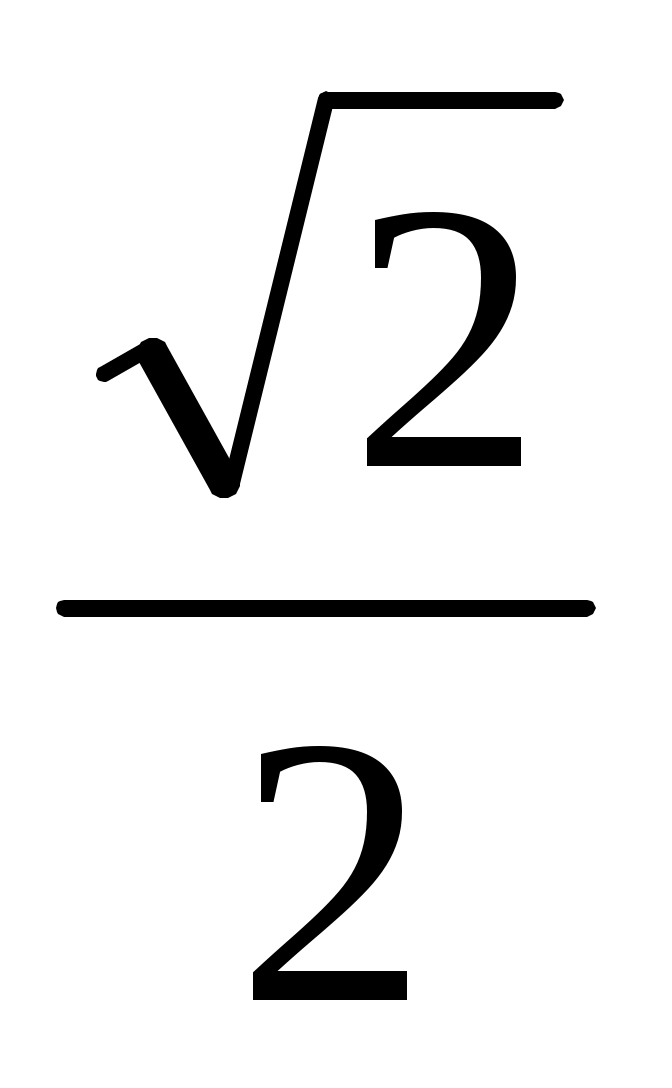 , если , если 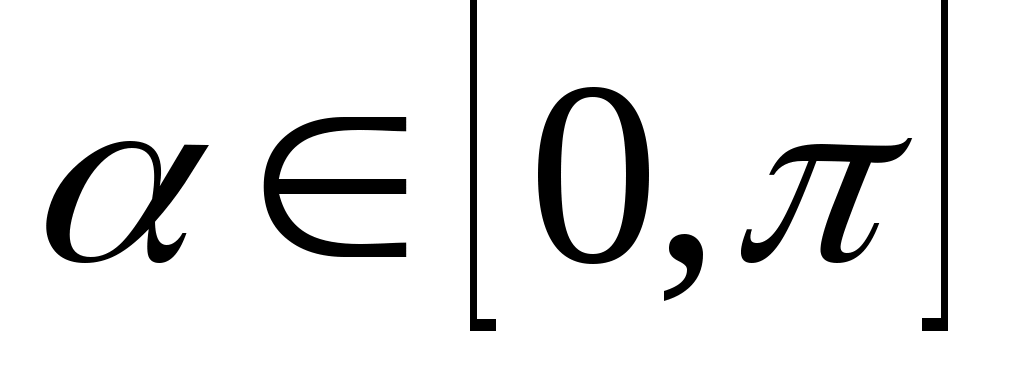 ? ?
4. Постановка темы и цели урока
5.Изучение нового материала
Учитель
|
Ученик
|
Теперь решим уравнение cos t =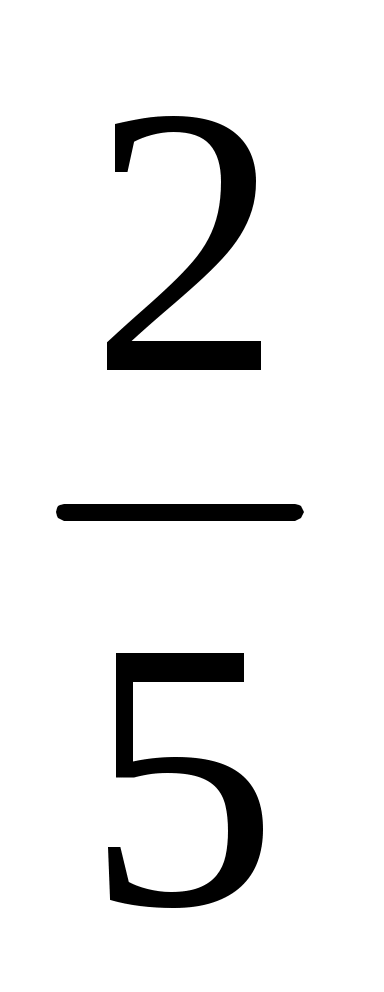 . .
|
на доске ведет запись на основной доске рядом с примером cos t = 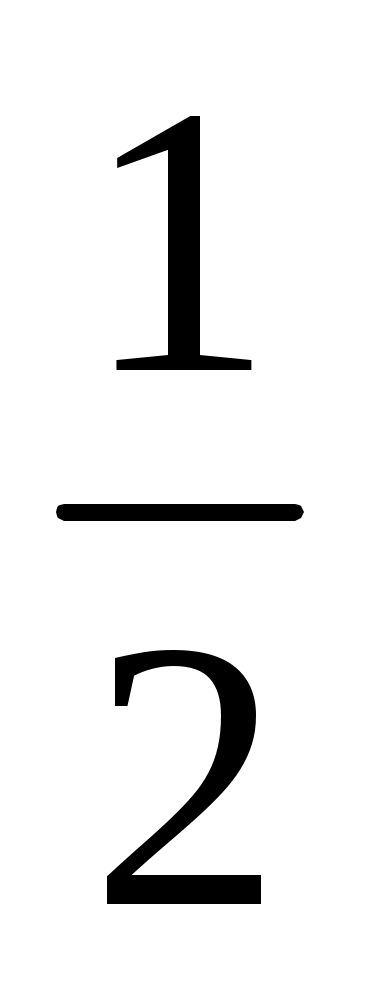 , все остальные учащиеся слушают (пример и единичная окружность записаны заранее) , все остальные учащиеся слушают (пример и единичная окружность записаны заранее)
Проговаривая алгоритм решения простейшего тригонометрического уравнения, ученик решает уравнение с помощью единичной окружности.
t = t1 +2πk, t = t2 +2πk, где k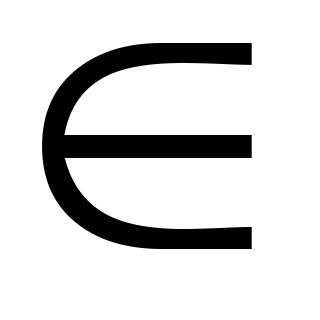 Z, т.к. t1= - t2, то t = ± t1 +2πk, где k Z, т.к. t1= - t2, то t = ± t1 +2πk, где k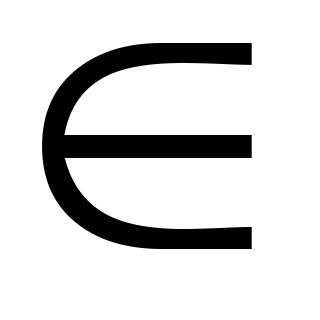 Z, Z,
|
Является ли эта записьответомрешения уравнения?
|
Эта запись не является ответом решения уравнения, т. к. не определены значения t1.
|
Учитель: Что это за число t1, пока неизвестно, ясно только то, что t1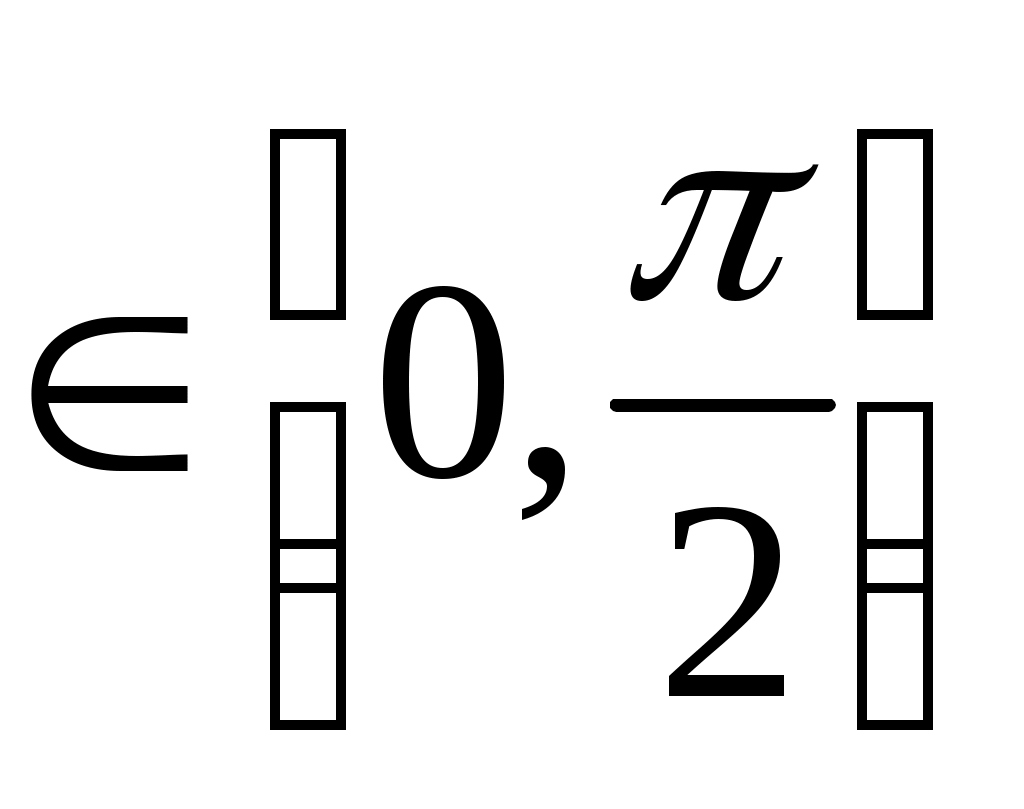 . Столкнувшись с такой ситуацией, математики поняли, что надо придумать способ ее описания на математическом языке. Поэтому был введен на рассмотрение новый символ arcсos а, который читается: арккосинус а. . Столкнувшись с такой ситуацией, математики поняли, что надо придумать способ ее описания на математическом языке. Поэтому был введен на рассмотрение новый символ arcсos а, который читается: арккосинус а.
Запишем тему сегодняшнего урока: «Арккосинус числа а. Решение уравнений cos t = a»
Учитель
|
Сегодня на уроке мы изучим понятие арккосинус числа а, научимся его вычислять и применять при решении простейших тригонометрических уравнений.
Arcus в переводе с латинского значит дуга, сравните со словом арка. Символ arcсosа, введенный математиками, содержит знак (arc), сosа - напоминание об исходной функции
|
Открываем учебник на стр.89 и читаем определение арккосинуса (ученики открывают учебник и читают по книге определение, выделяя главное)
|
Закрепление и отработка понятия арккосинус числа а и алгоритма его вычисления (фронтальная работа с классом)
Учитель
|
Ученик
|
Значит, вычисляя арккосинус числа а, какой нужно себе задать вопрос?
|
Косинус какого числа равен а?
|
Применяя изученное определение, найдите значение выражения
arccos (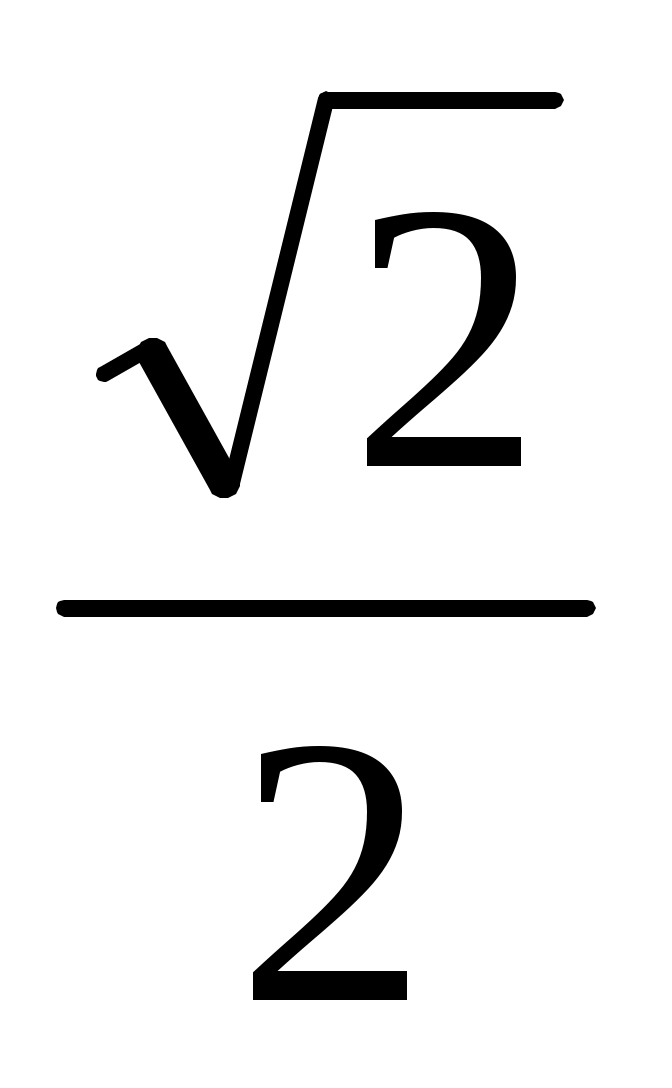 );arcсos( );arcсos( 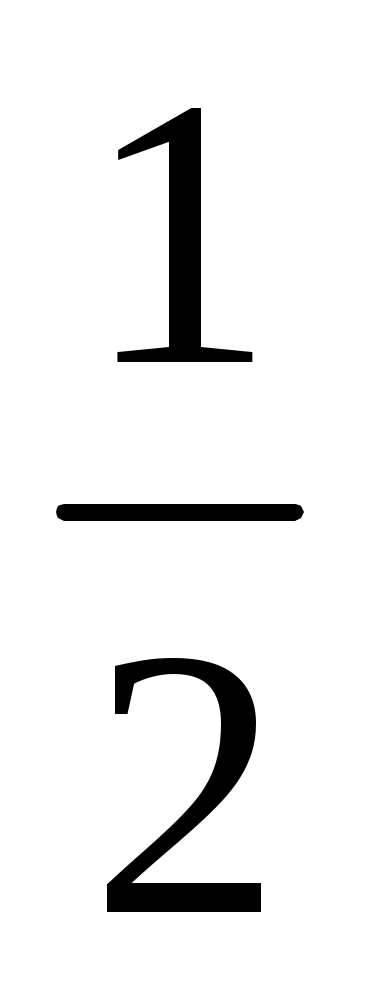 ) arcсos( ) arcсos( 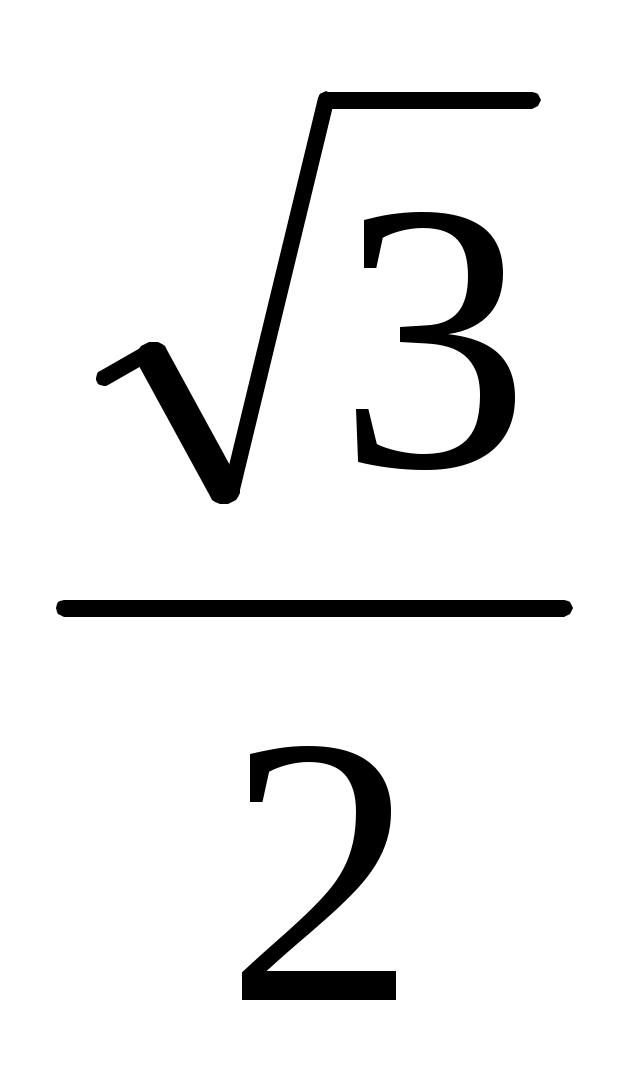 ) (Слайд 5) ) (Слайд 5)
|
arccos (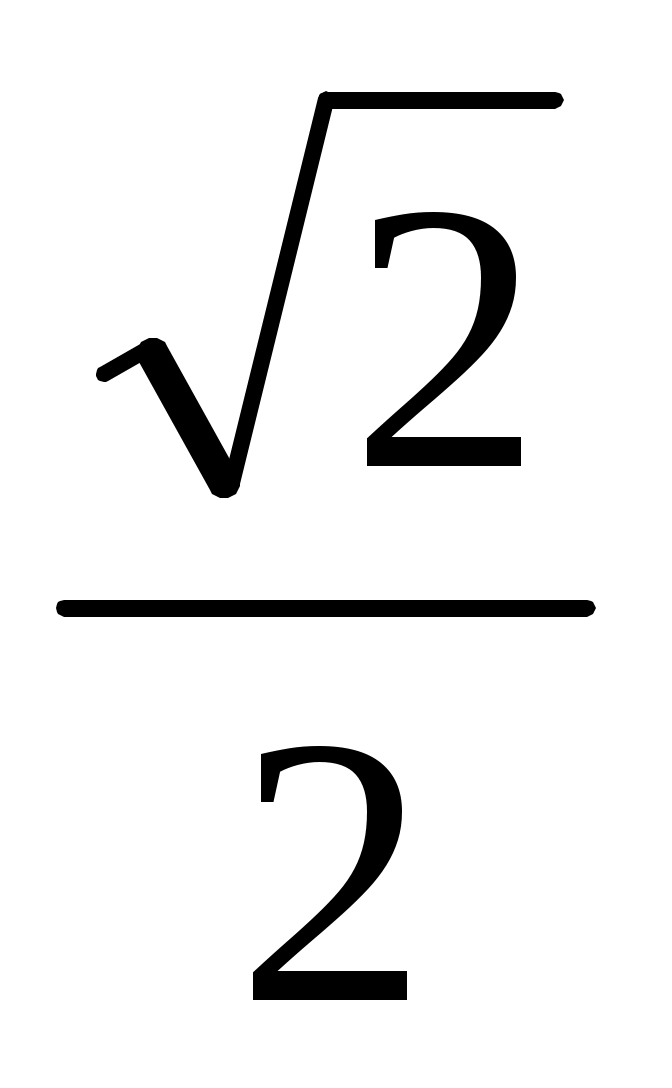 ) = ) =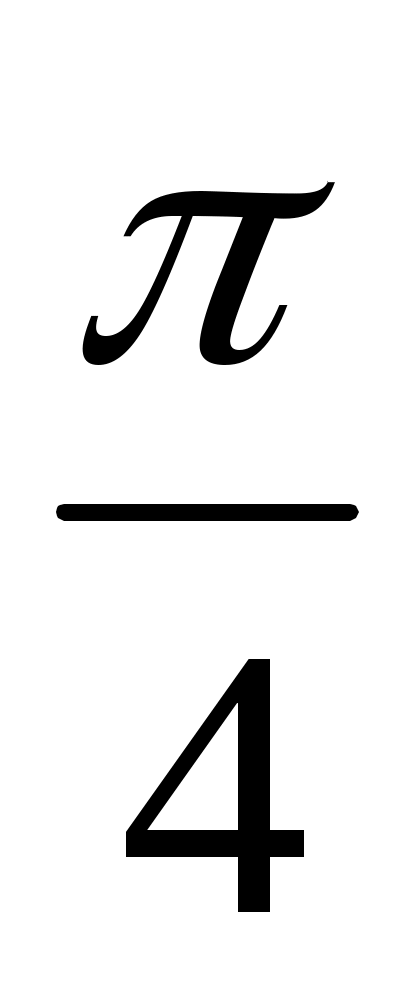
arcсos(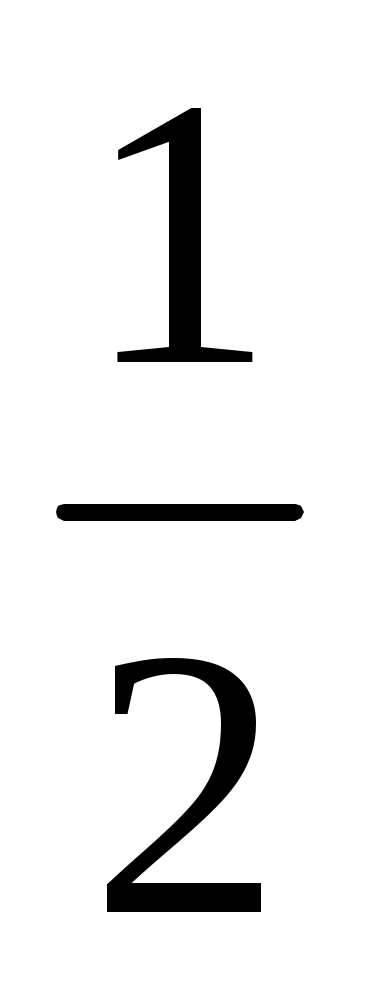 ) = ) =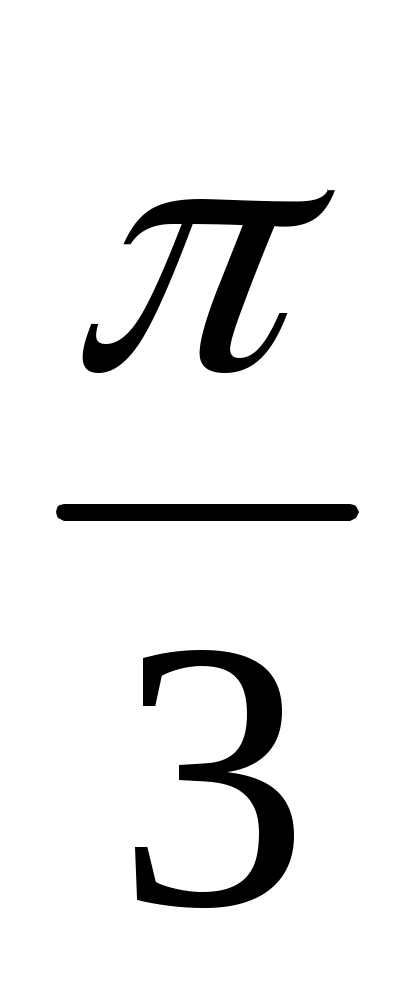
arcсos( 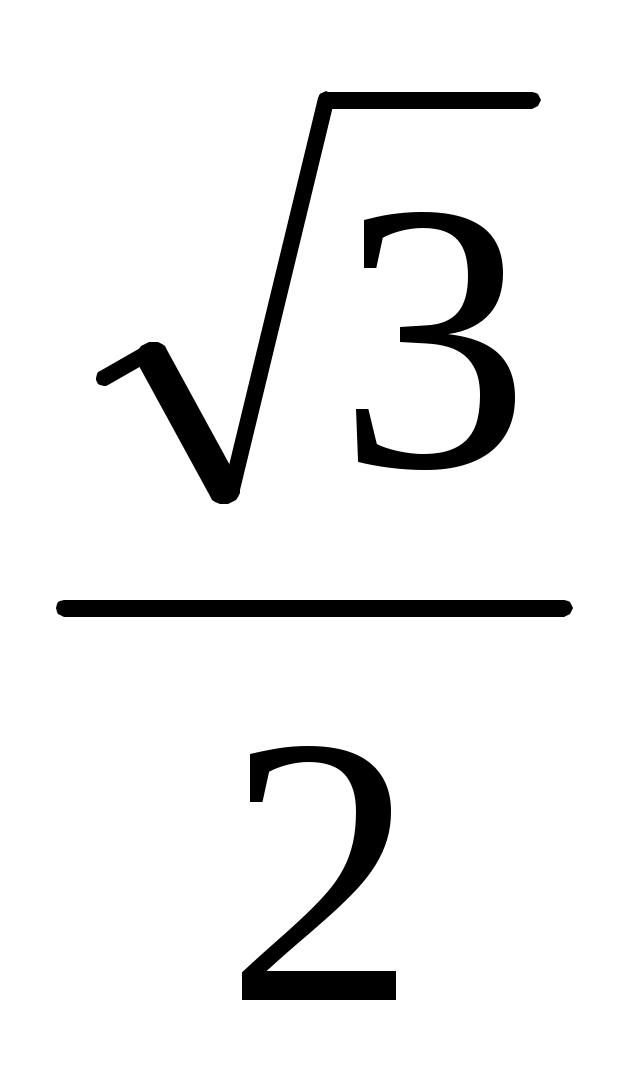 ) = ) =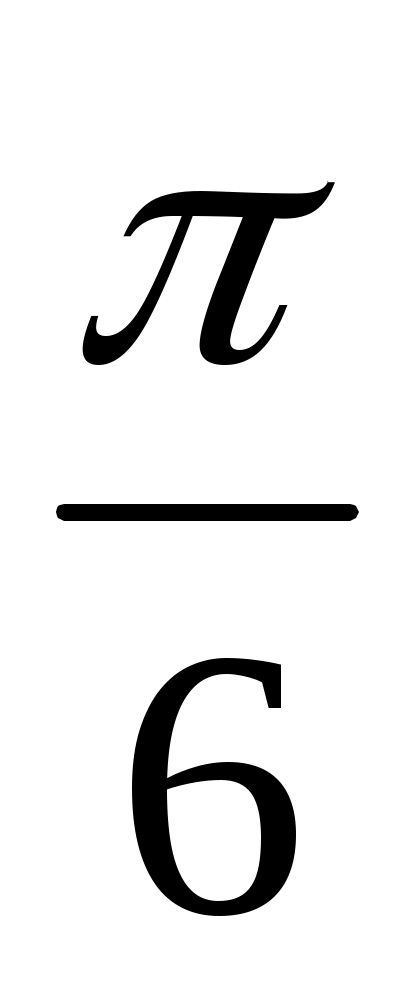
|
Все значения а принадлежат отрезку от -1 до 0. Какой четверти принадлежат значения арккосинуса а?
|
Значения arccosа принадлежат отрезку от 0 до 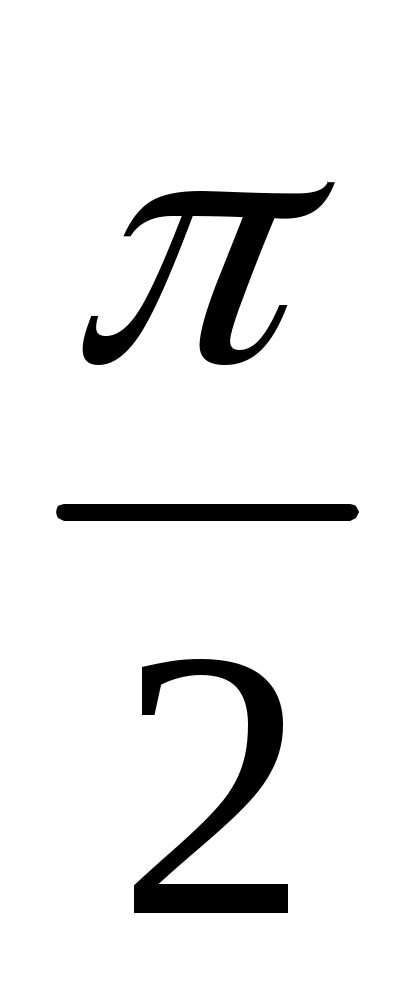
|
А как же вычислить значение arccos(–а)? Обратимся к учебнику и найдем формулу, по которой вычисляется значение arccos(–а) (читаем и выделяем формулу). (Слайд 6)
Вычислить: arccos (-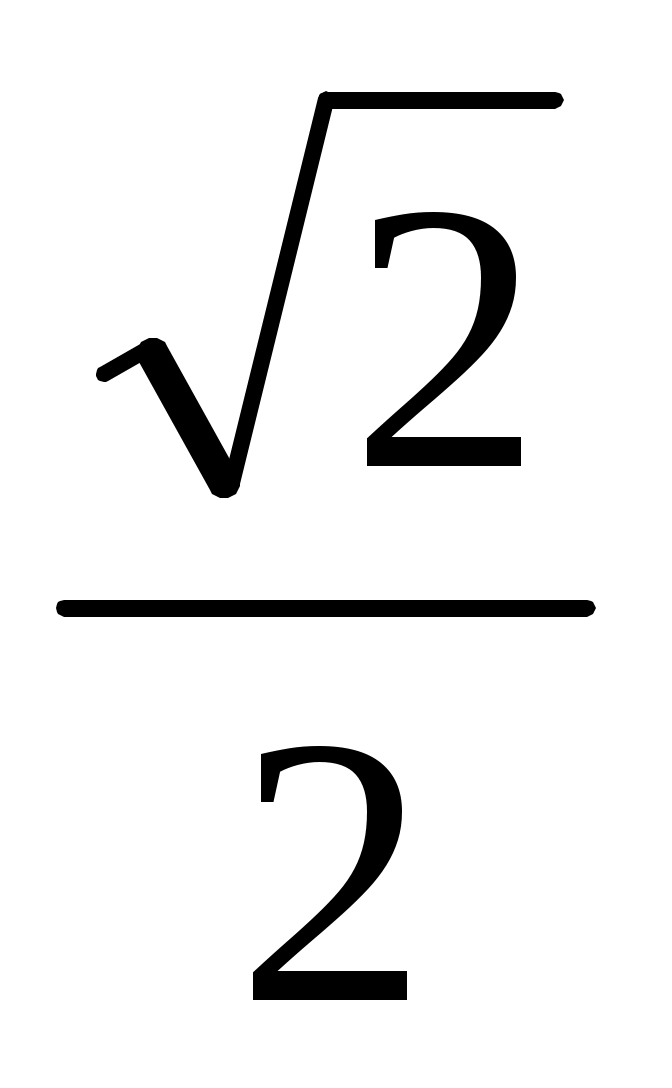 ); arcсos(- ); arcсos(- 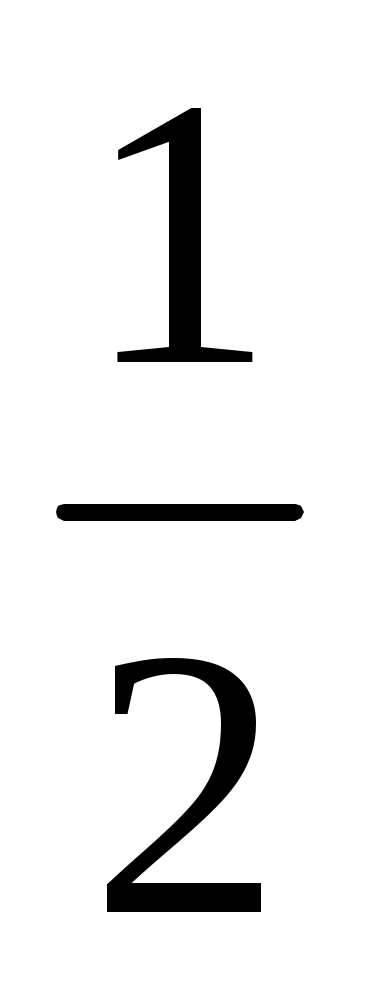 ); arcсos(- ); arcсos(- 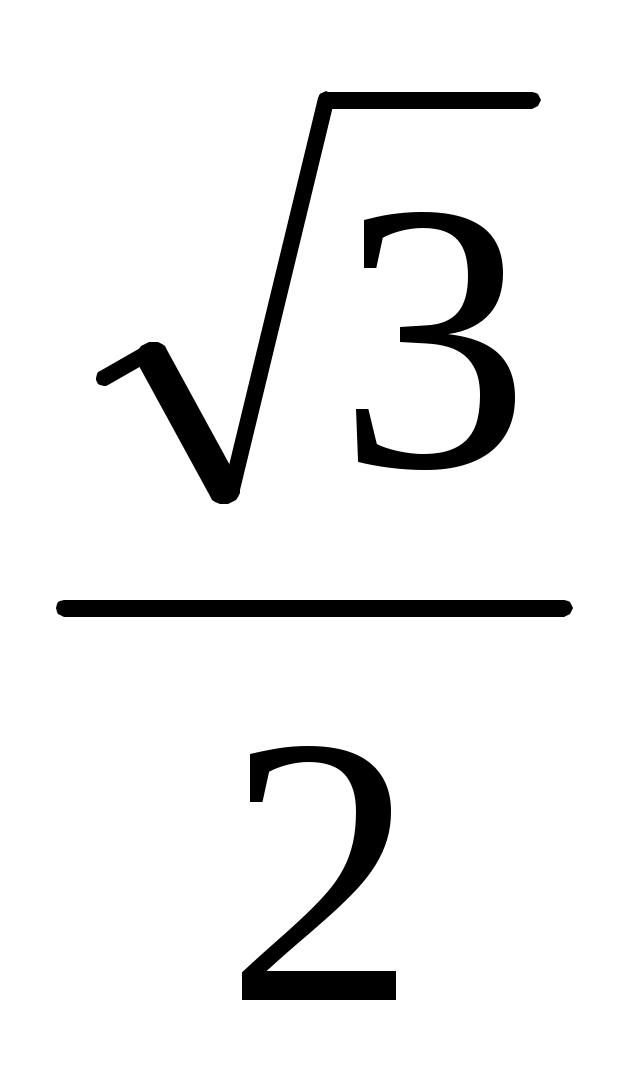 ); (Слайд 6) ); (Слайд 6)
|
arccos (-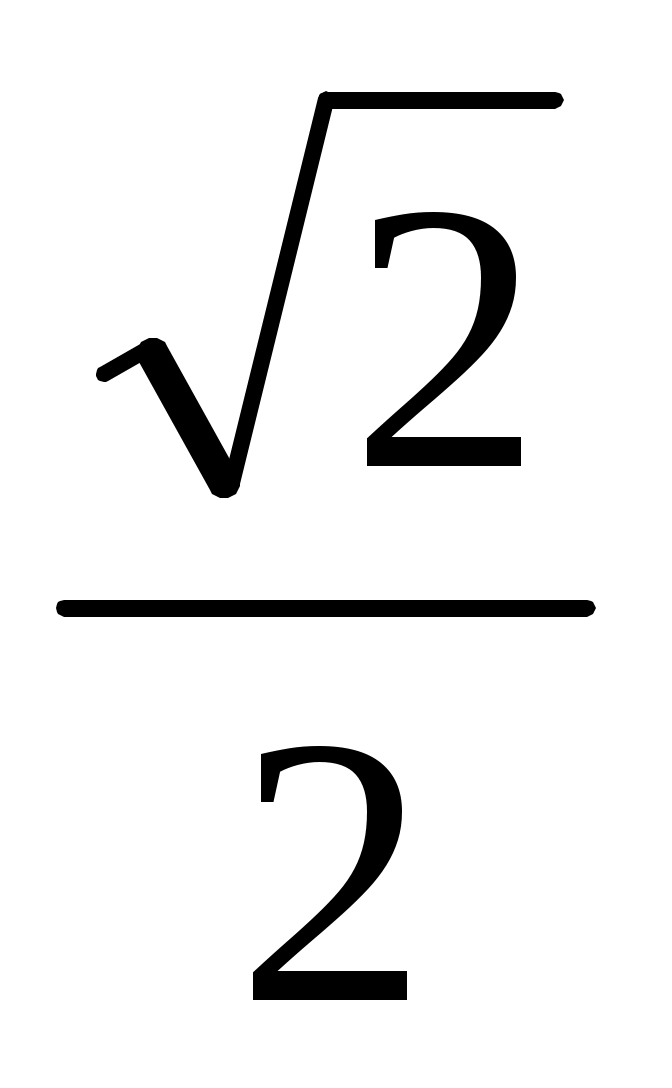 )= )= 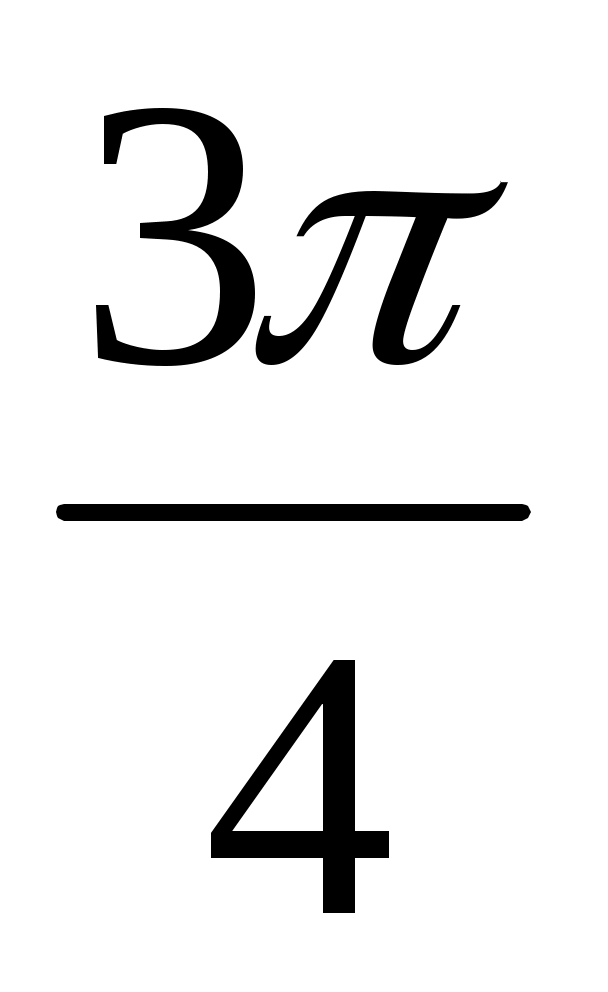
arсcos(- 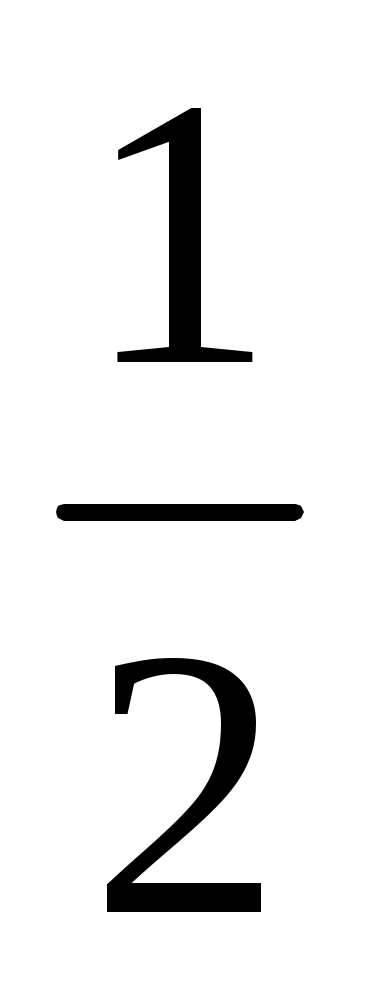 ) = ) = 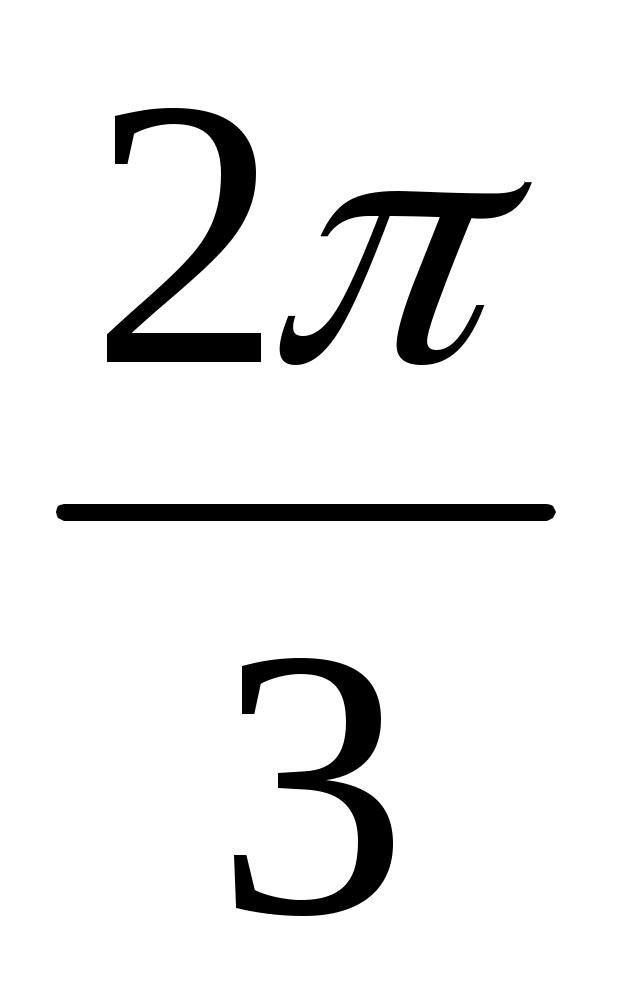
arсcos(- 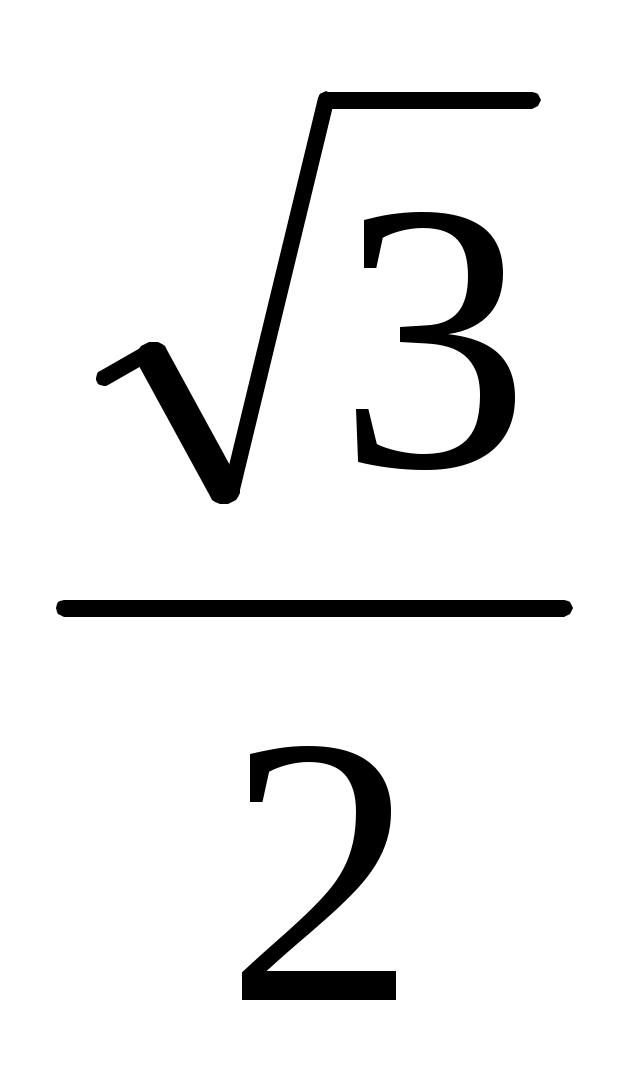 ) = ) =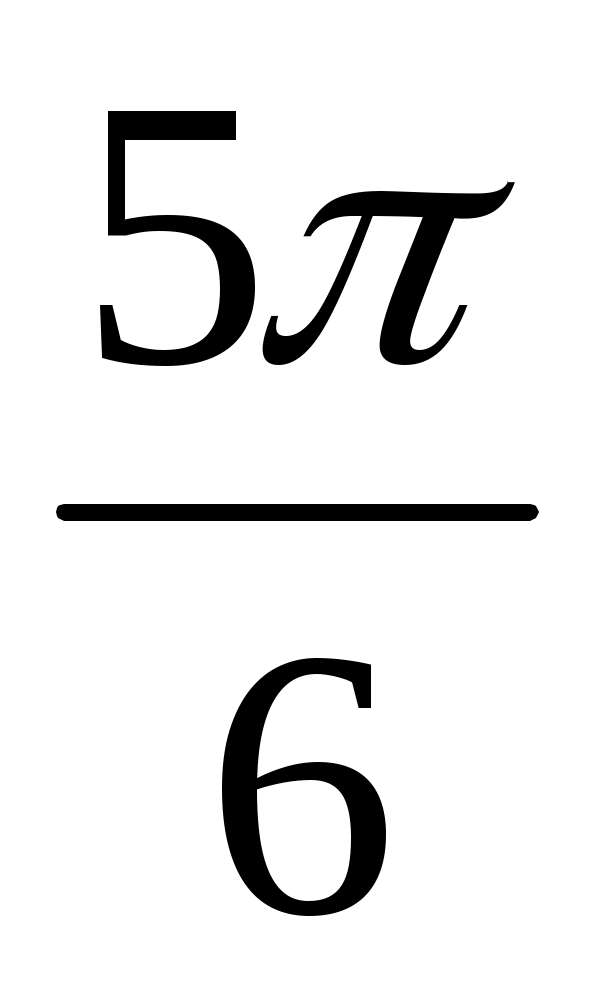
|
Все значения (-а) принадлежат отрезку от -1 до 0. Какой четверти принадлежат значения arccos(–а)?
Запишите справочный материал (слайд 6)
|
Значения arcсos(-а) принадлежат отрезку от 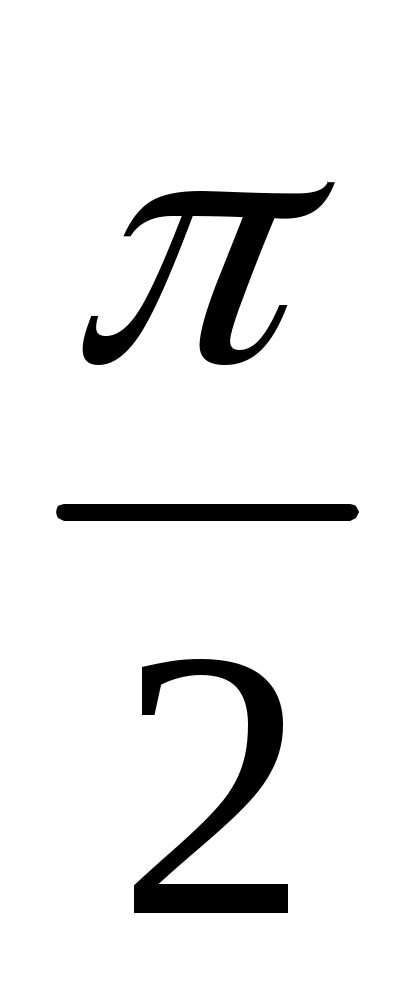 до π до π
Учащиеся записывают формулу в тетрадь.
|
5. Закрепление изученного материала.
Задание
|
Найти значение выражения:
а) arccos (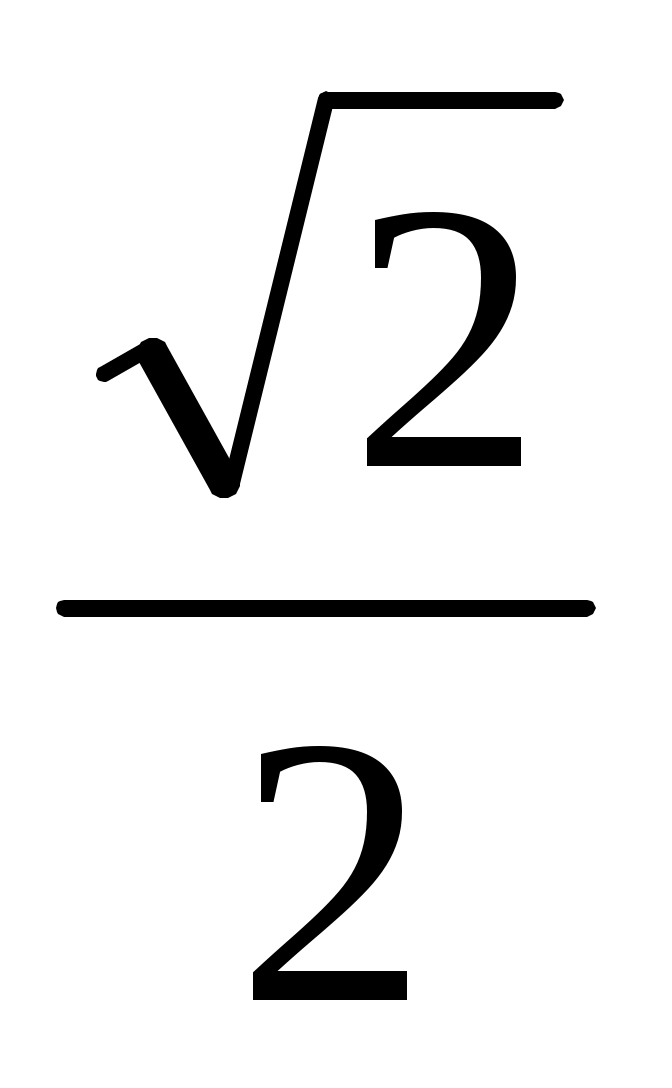 )-arccos (- )-arccos (-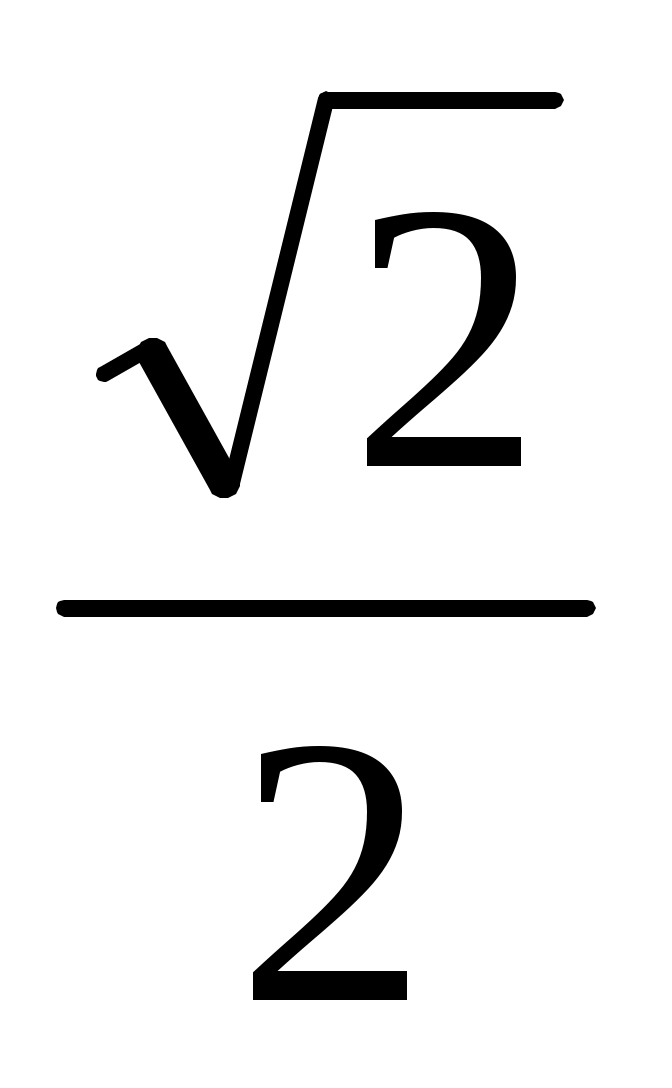 )+ )+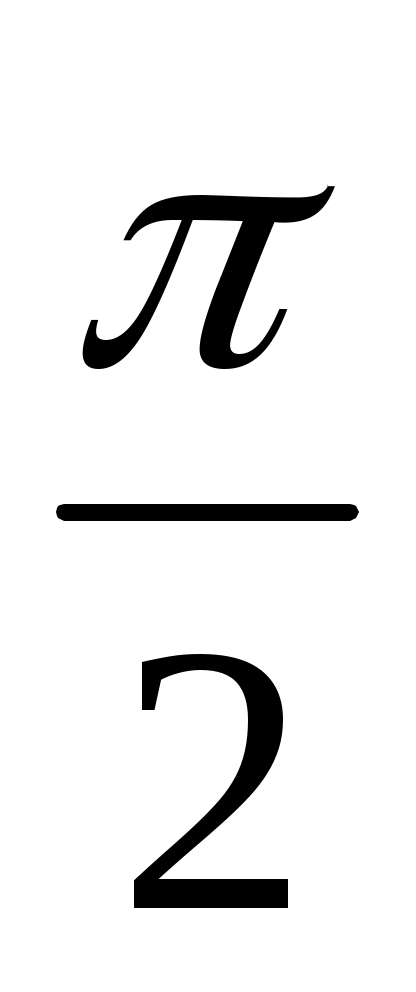 +arcos1 +arcos1
|
б) 2arccos 0 + 3 arccos 1 –arcos (-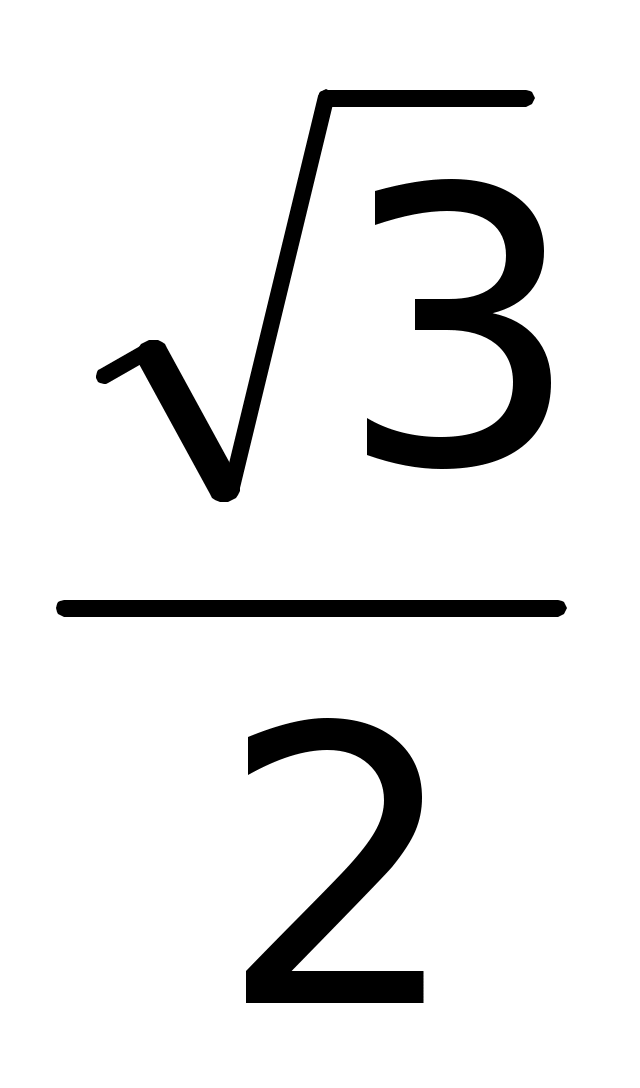 ) )
|
6. Самостоятельная работа (с последующей самопроверкой)
2 человека работают у доски самостоятельно, остальные работают в тетрадях, затем проверяют правильность выполнения. Те, кто работал с дом заданием, у доски пишут налисточка, затем сдают их на проверку
Учитель
|
Ученик
|
Вернемся к уравнению cos t =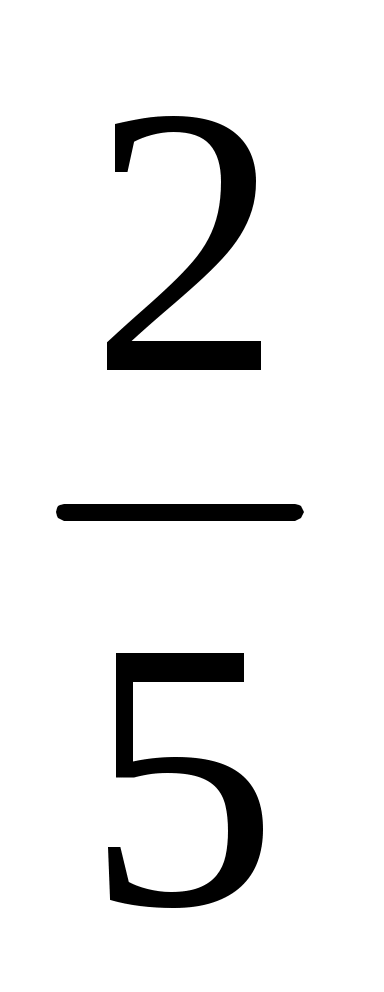 . которое решала…. Зная понятия арккосинуса, теперь мы можем записать ответ решения этого уравнения следующим образом. . которое решала…. Зная понятия арккосинуса, теперь мы можем записать ответ решения этого уравнения следующим образом.
cos t =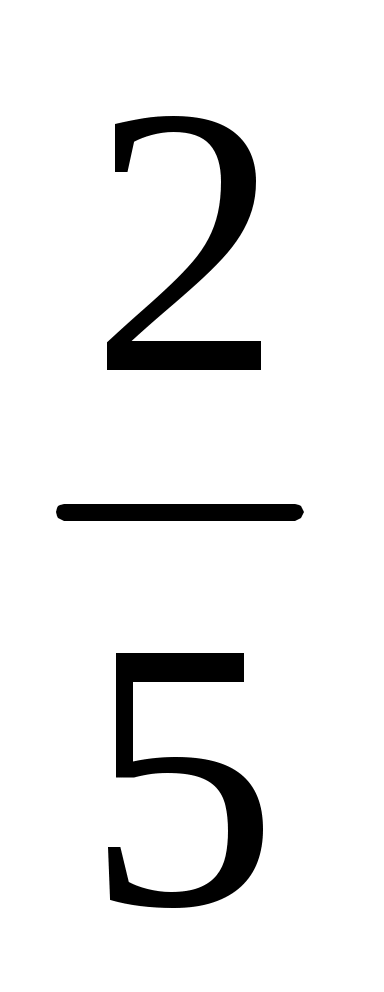 . .
t = ±arccos 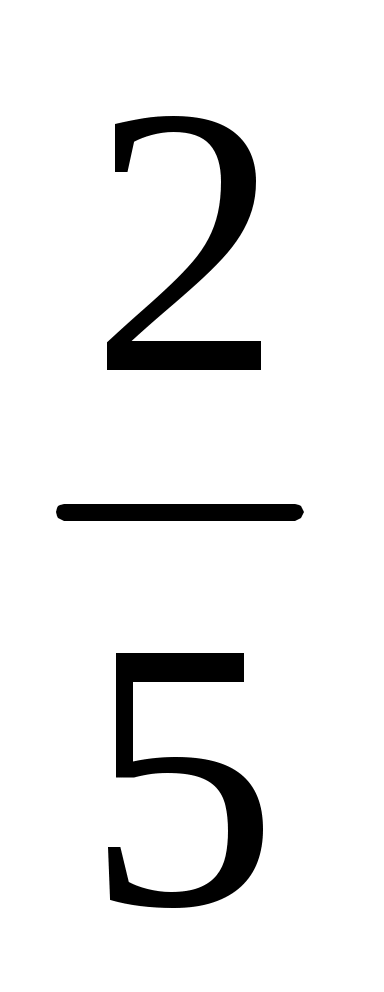 + 2πk, где k + 2πk, где k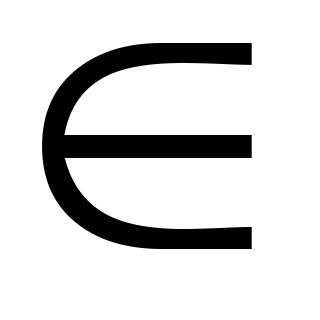 Z . Z .
Ответ: t = ±arccos 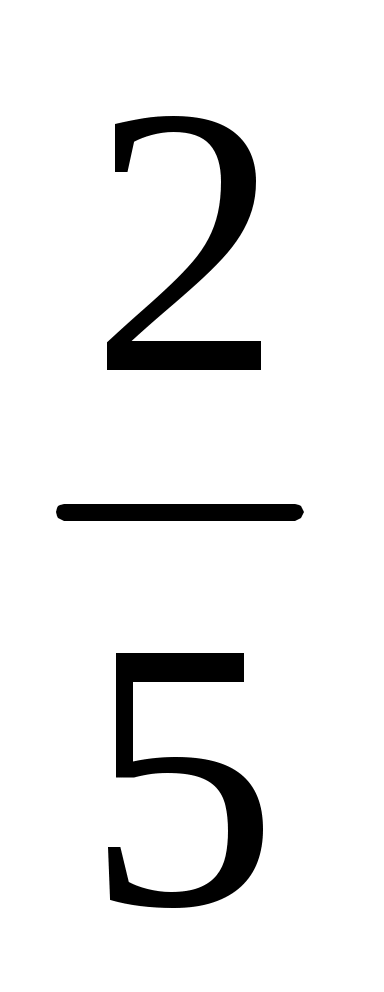 + 2πk, где k + 2πk, где k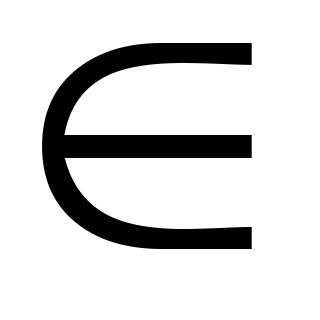 Z Z
Мы решили уравнение двумя способами: с помощью единичной окружности и с помощью формулы.
|
Записывают в тетради решение за учителем
|
Итак, запишем справочный материал и выделим его решением уравнения (Слайд 10)
cos t = a, где а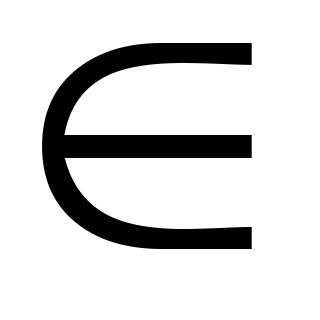 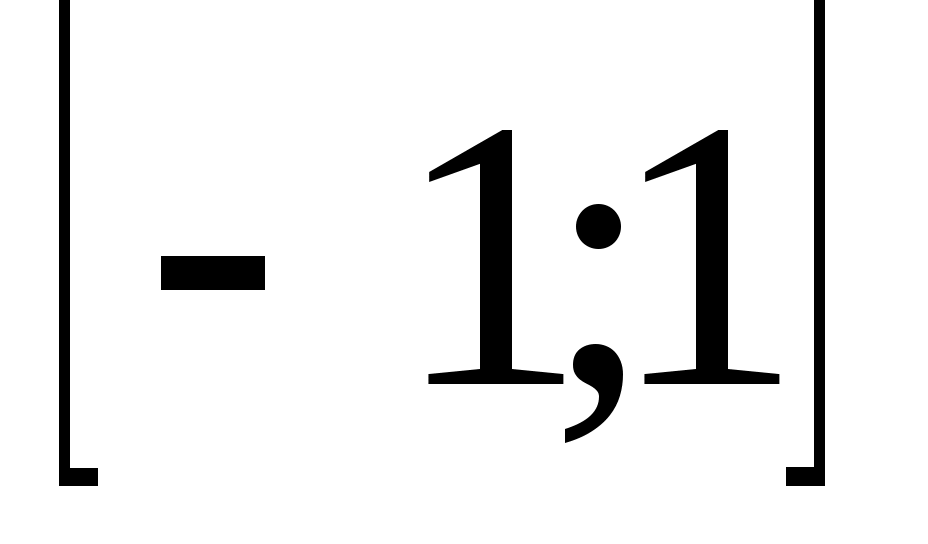 . .
t = ± arcсos а + 2πk, k . .
Ответ: t = ± arcсos а + 2πk, k . .
|
Записывают в тетради модель решения уравнения за учителем
|
1 уч.: а) cos t = 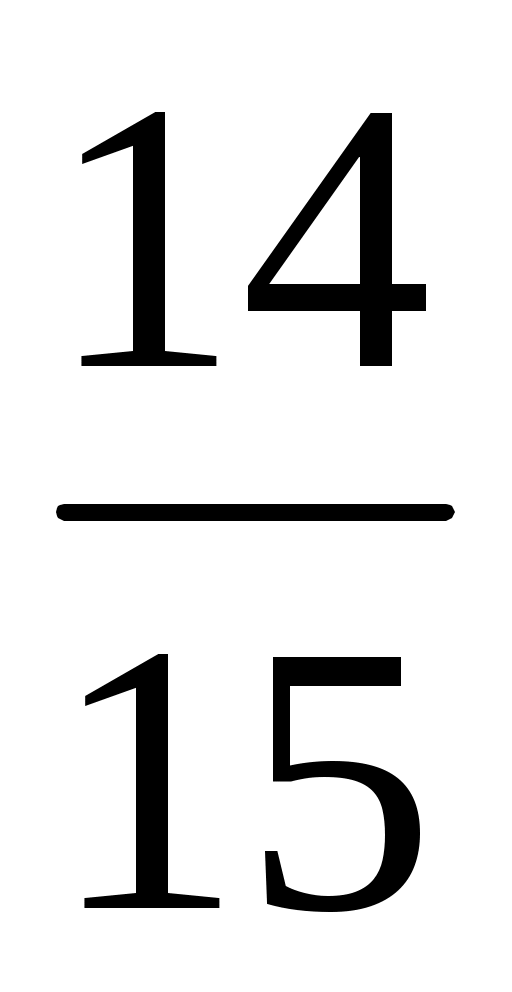 ; б) cos t = - ; б) cos t = -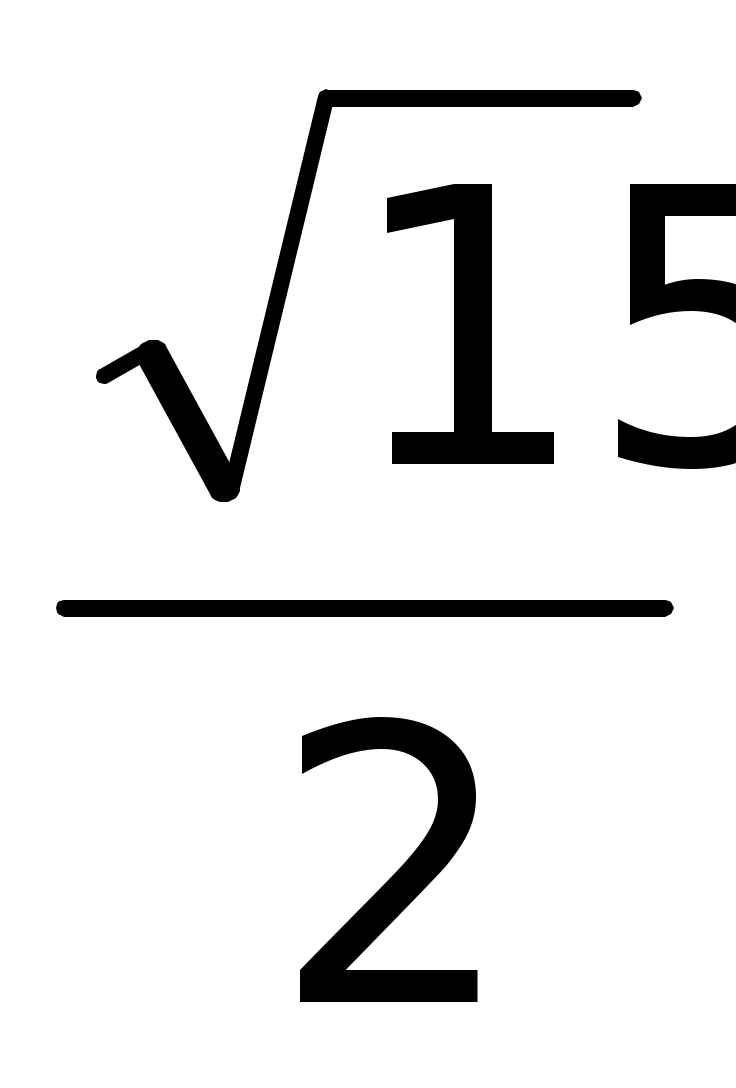 ; ;
2 уч: а) cos t = 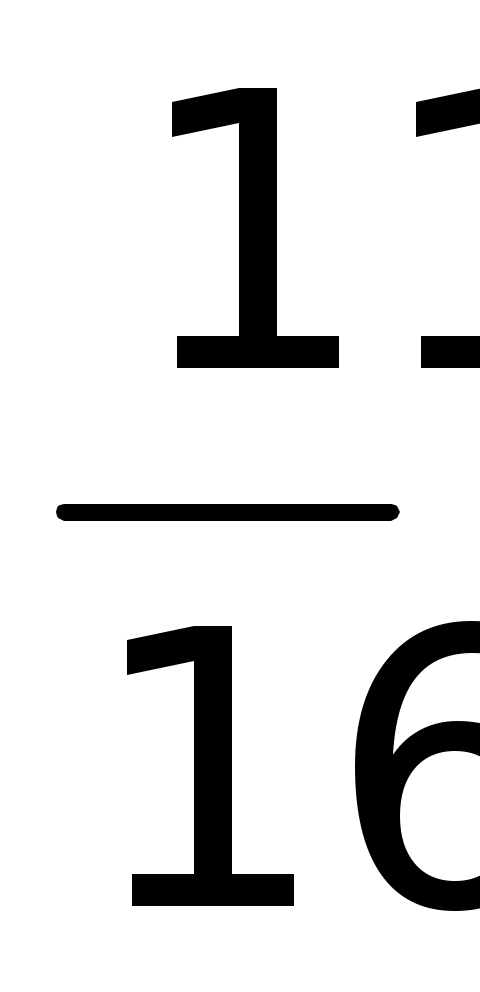 ; б) cos t = ; б) cos t = 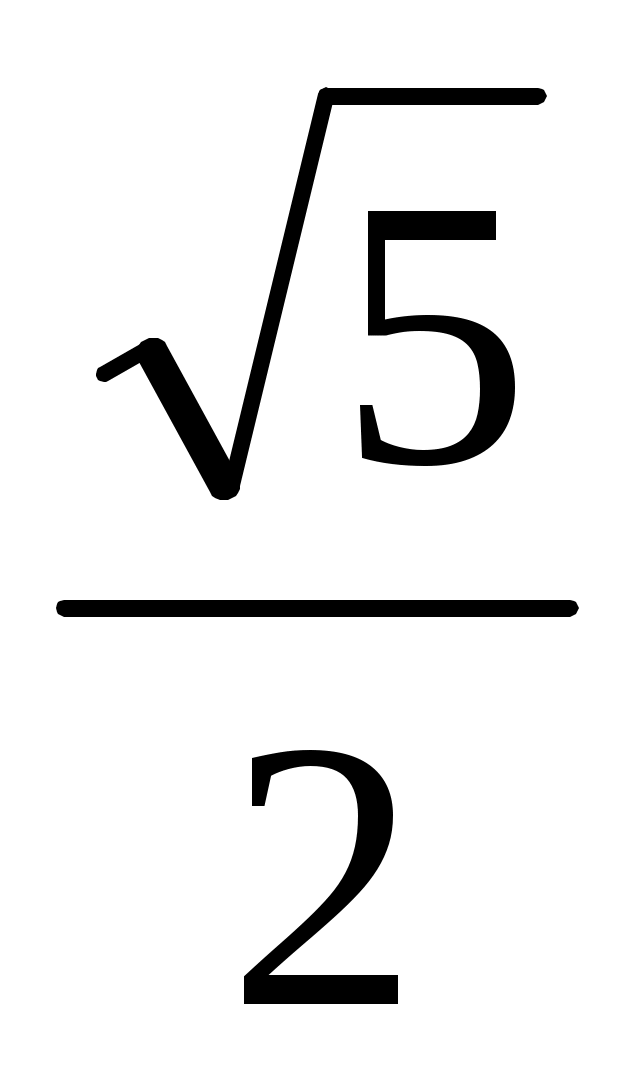 . (обратить внимание на этот пример, выполняя оценку числа . (обратить внимание на этот пример, выполняя оценку числа 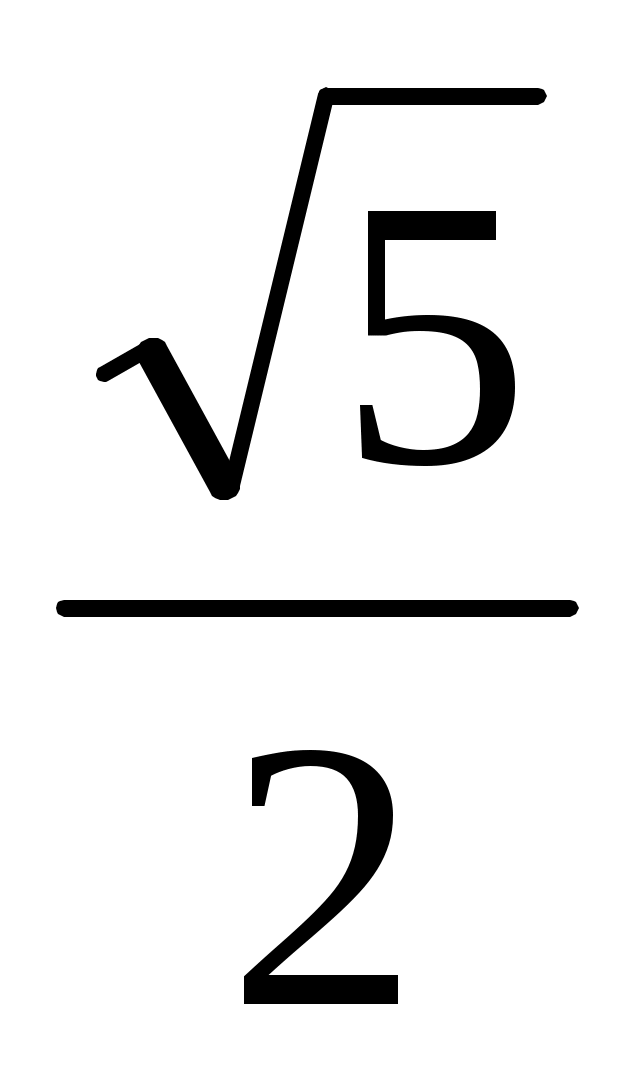 ) )
Решите уравнение:
№2
б) cos t = 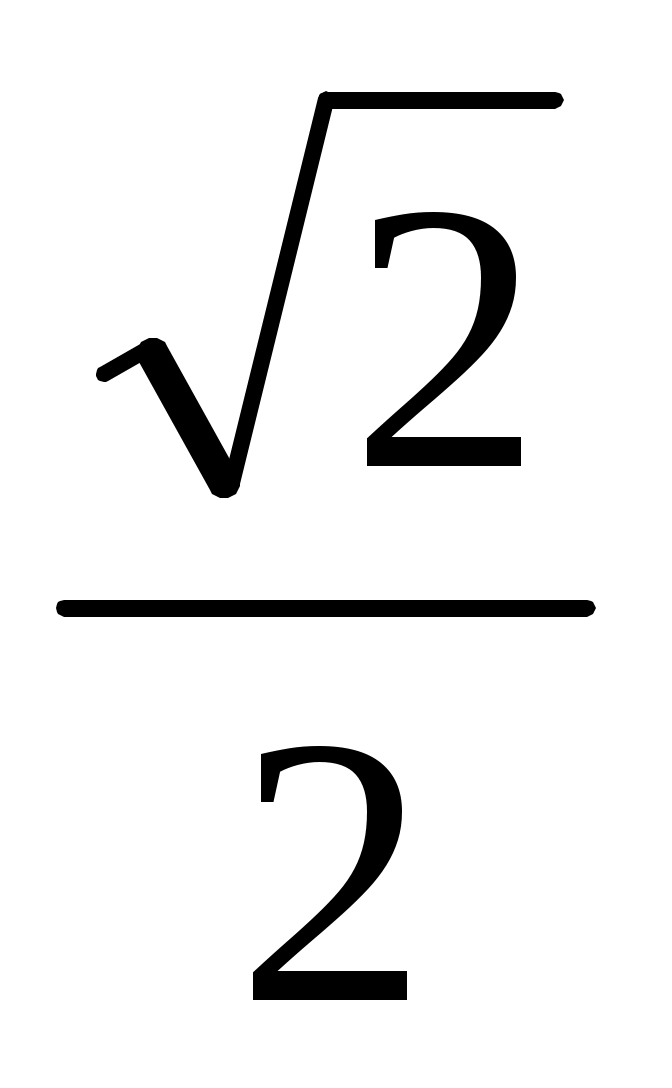 . .
г) cos t = 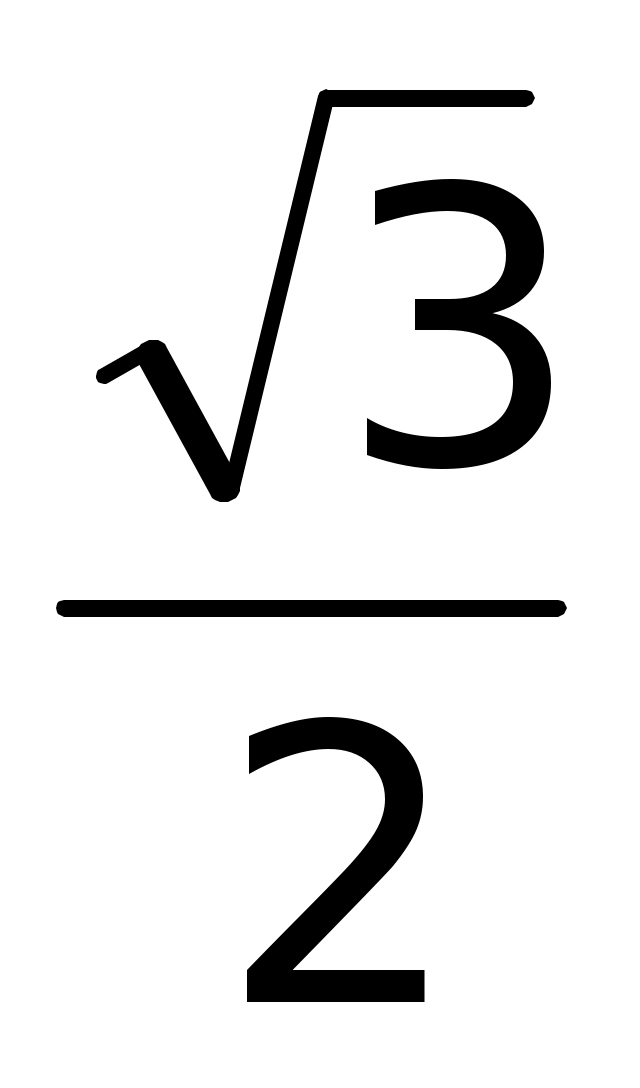 ; ;
№3
а) cos t =1; (обратить внимание на ответ и выделить частные случаи)
б) cos t = -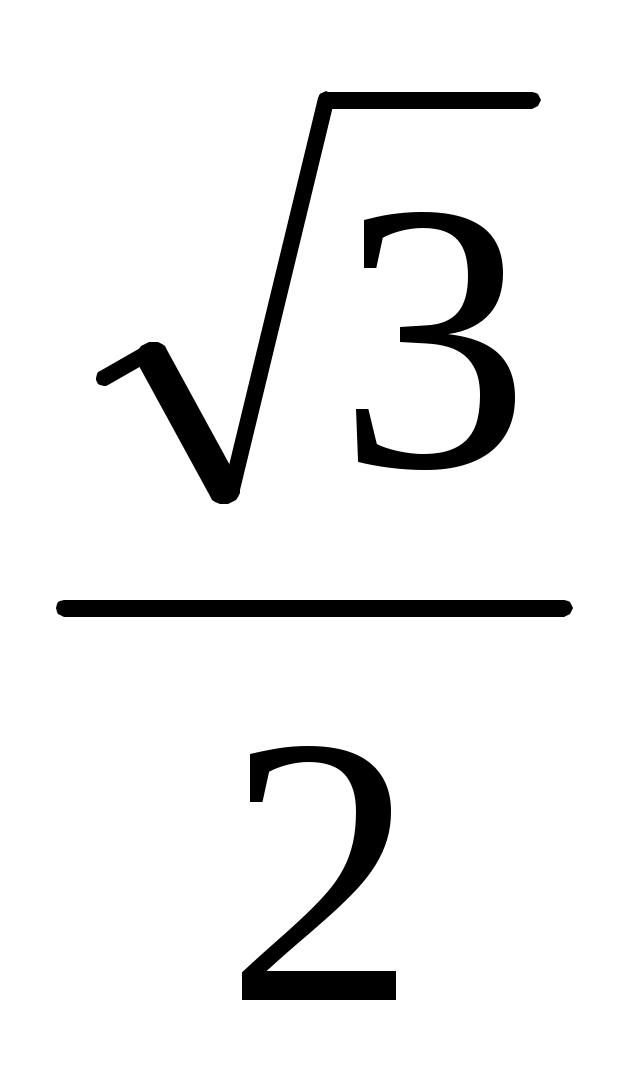
6. Подведение итогов урока
7.Домашнее задание
       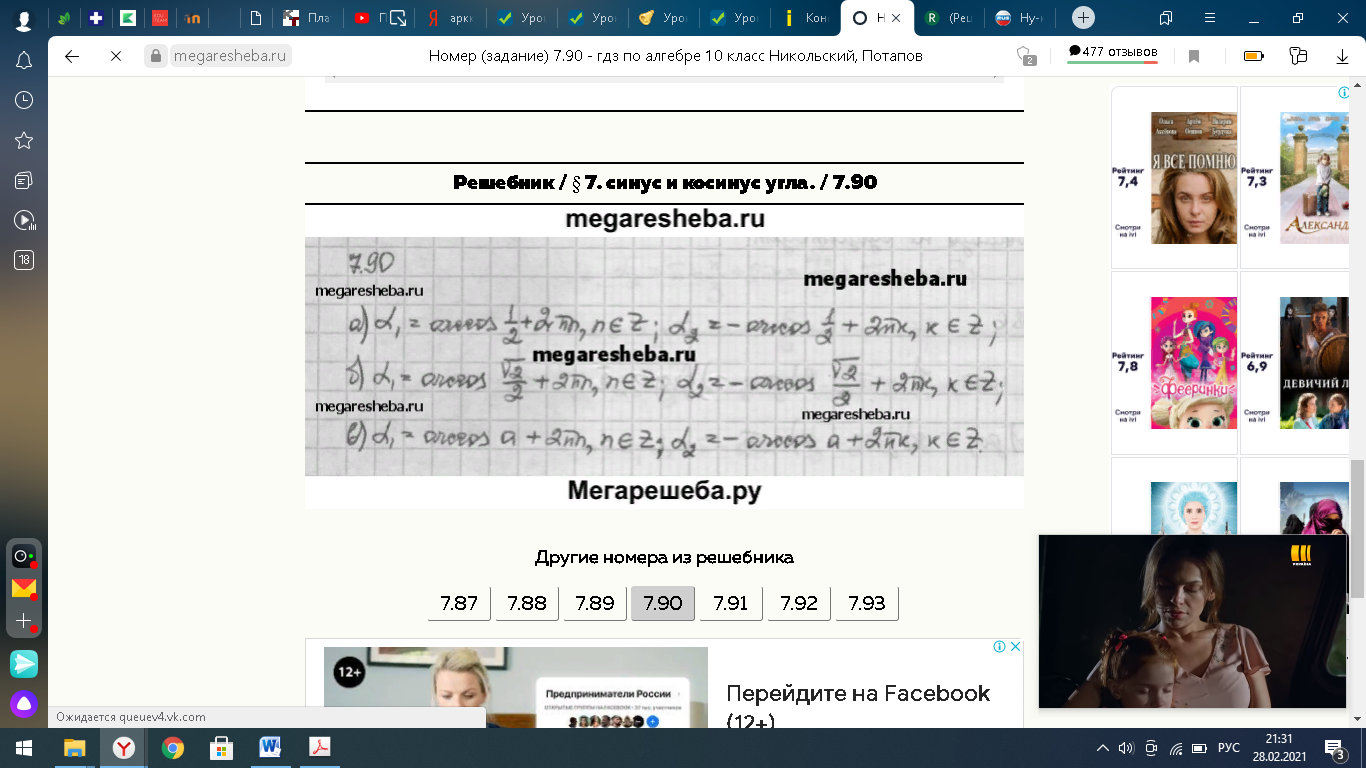 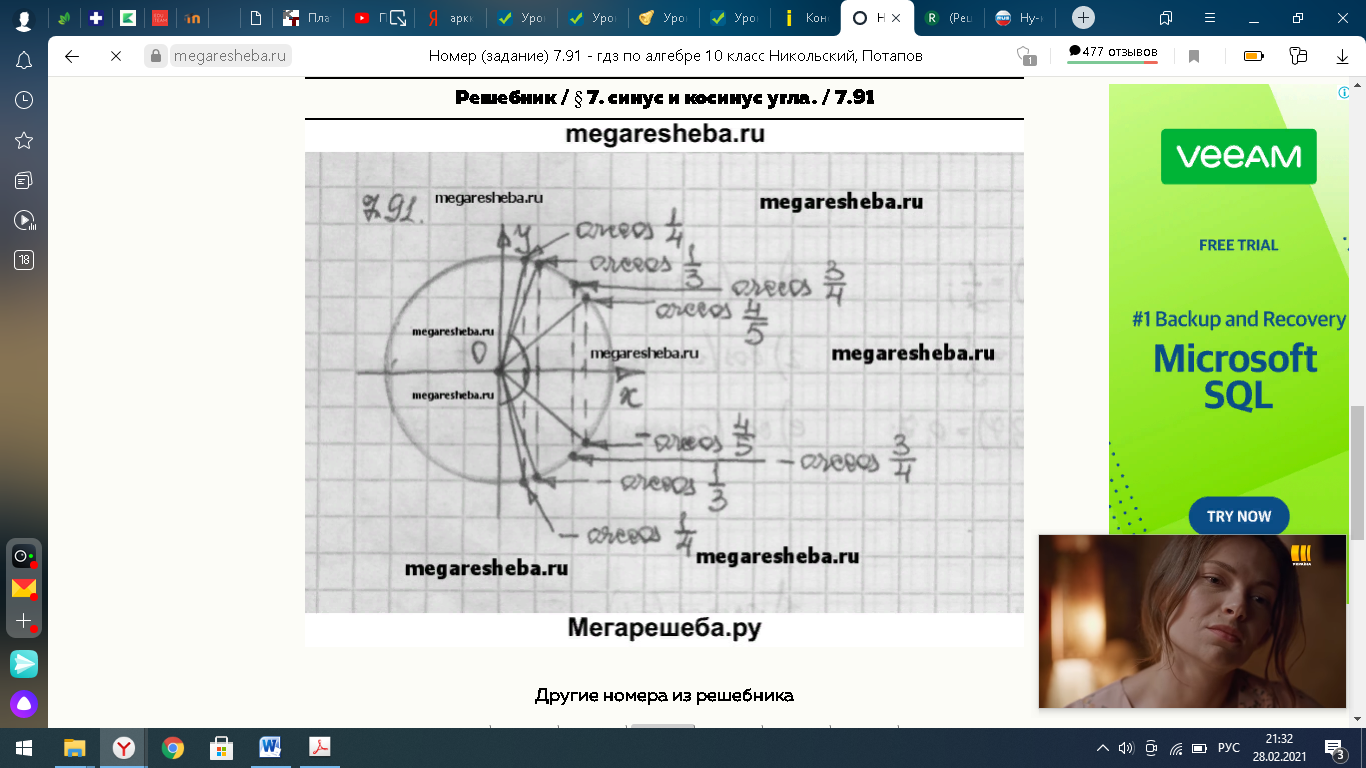
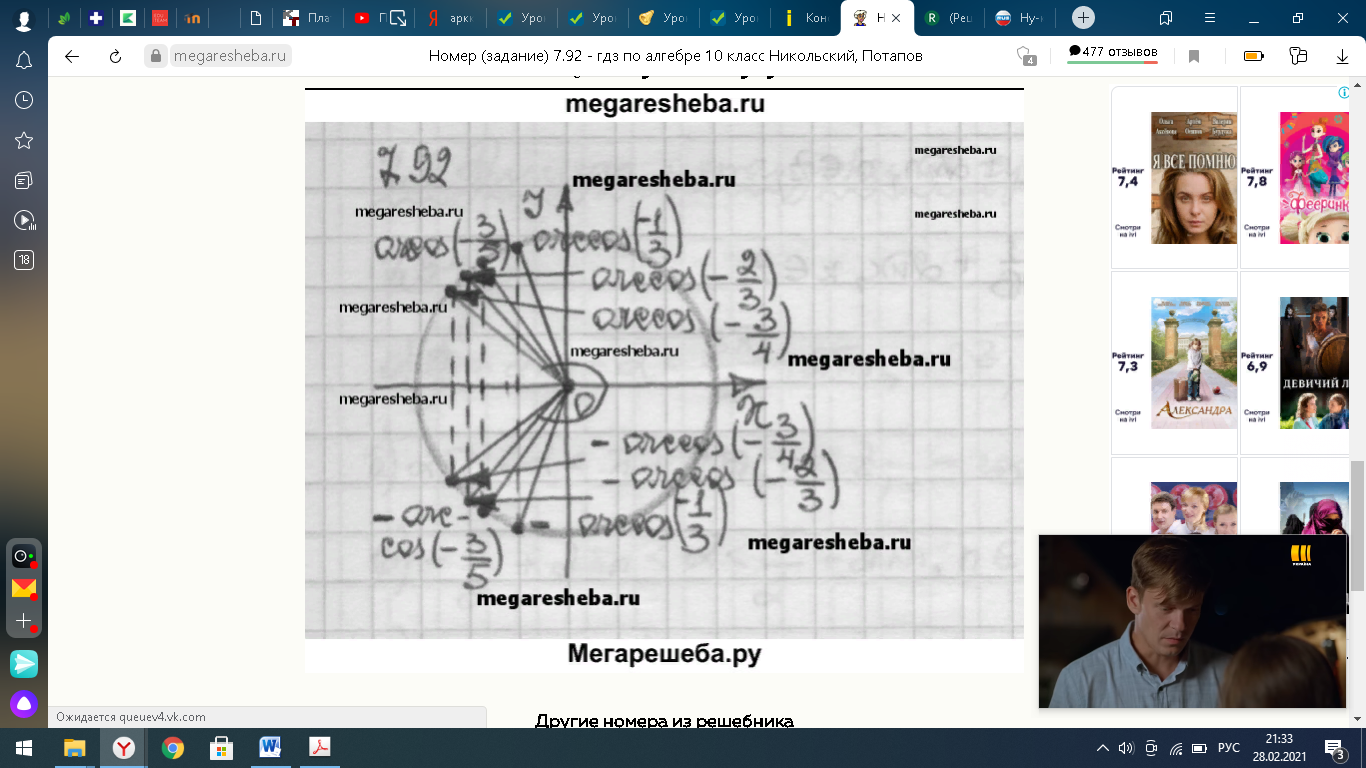 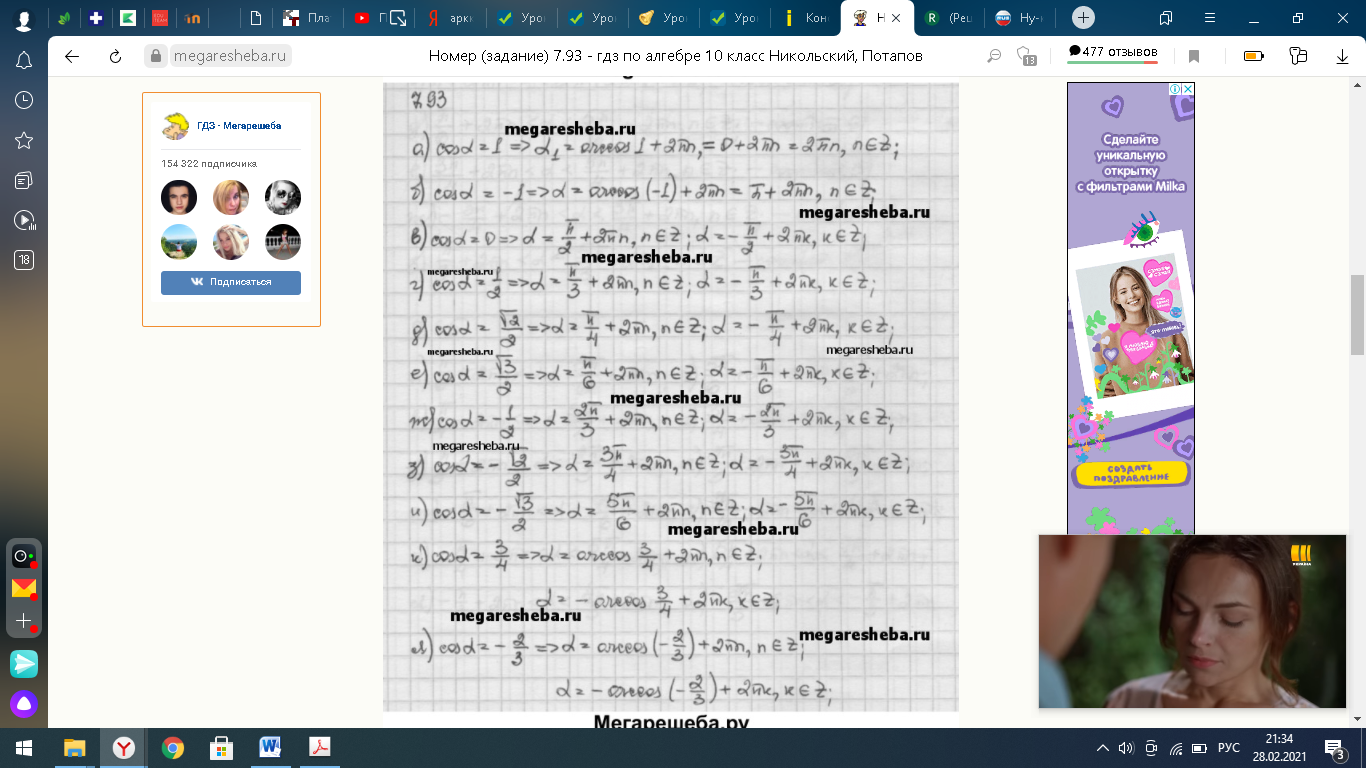 |
|
|
 Скачать 6.37 Mb.
Скачать 6.37 Mb.










