Автономное образовательное учреждение лицей 14 имени Заслуженного учителя Российской Федерации А. М. Кузьмина Формула Пика
 Скачать 0.78 Mb. Скачать 0.78 Mb.
|
|
Муниципальное автономное образовательное учреждение лицей №14 имени Заслуженного учителя Российской Федерации А.М. Кузьмина Формула Пика Выполнил: ученик 10 А класса Лазарев Данил Научный руководитель: Неверовская Светлана Владимировна Тамбов 2015 ОглавлениеВведение. 3 1.Основная часть. 4 1.1. Целочисленные решетки. 4 1.2. Правильные многоугольники 7 1.3. Формула Пика. 10 1.4. Подсчет узлов на отрезке с вершинами в узлах сетки. 12 Вывод. 16 Список литературы. 17 Введение.Моя работа посвящена формуле Пика. Также я постараюсь больше рассказать о целочисленных решетках и триангуляции многоугольника. На данную тему я наткнулся при подготовке к олимпиаде, при решении олимпиадных задач. К одной из задач предлагалось два решения, одно из которых основывалось на формулу Пика. Заинтересовавшись этой формулой, я начал искать, применяется ли он где-то еще или же это был единичный случай. Как оказалось, она часто используется не только при решении олимпиадных задач, но даже и при решении задач из ЕГЭ и ГИА. После этого я решил обязательно изучить, как решать подобного рода задачи и вообще узнать больше об этой на тот момент неизвестной мне теореме. Начав собирать информацию об этом, я узнал, что для изучения формулы Пика, мне необходимо разобраться и в том, что такое целочисленные решетки. Актуальность: данная формула может помочь вам и при решении олимпиадных задач, и при решении задач из ГИА и ЕГЭ. Цель работы: исследовать формулу Пика и все темы, связанные с ней. Создать сайт, суммируя весь собранный материал, который поможет людям, желающим разобраться в этой теме. Разобрать примеры решения некоторых задач. Задачи: Изучить литературу по теме о целочисленных решетках Изучить литературу по теме формула Пика Разобраться в решении задач как простых, так и сложных Собрав все воедино, создать сайт, посвященный моей теме. Практическая значимость моего проекта состоит в возможности совмещения алгебры, геометрии и информатики. 1.Основная часть.1.1. Целочисленные решетки.Рассмотрим на плоскости сетку, образованную двумя семействами параллельных прямых, разрезающих плоскость на одинаковые параллелограммы_(рис.1). . 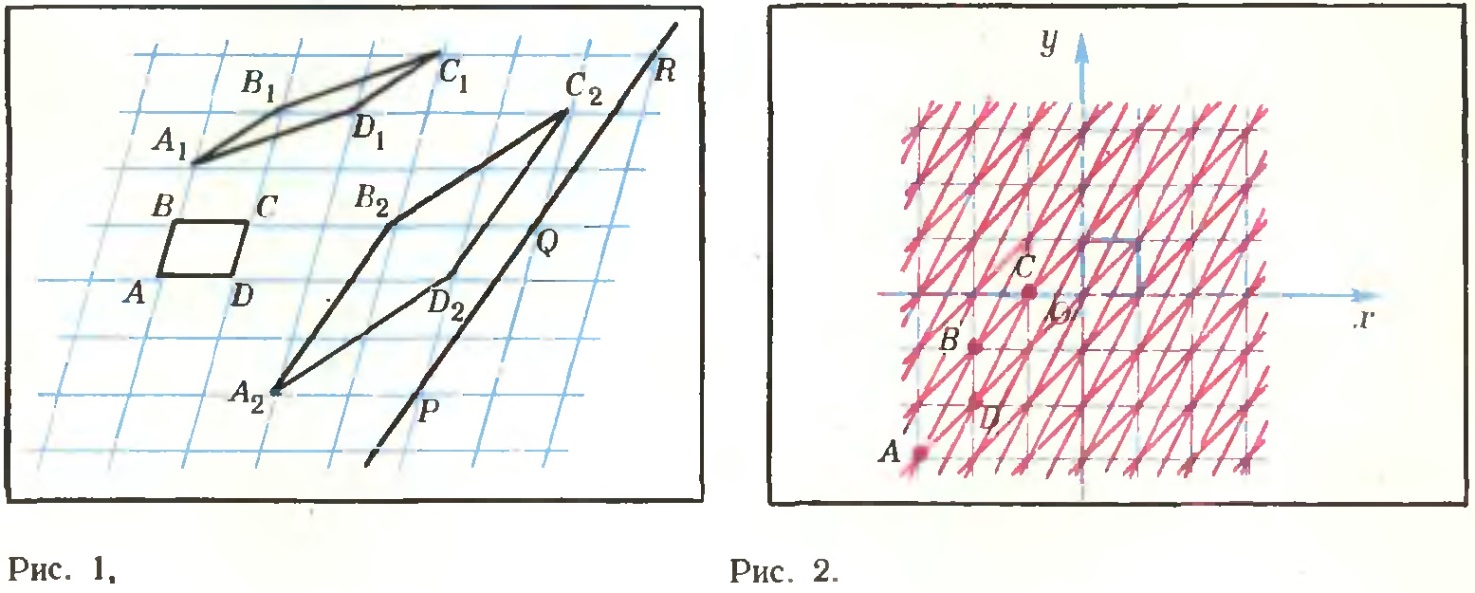 Множество всех вершин этих параллелограммов назовем точечной решеткой или целочисленной решеткой, сами вершины – узлами решетки, а любой из параллелограммов разбиения – основным параллелограммом разбиения, или параллелограммом, порождающим решетку. Заметим, что одна и та же решетка может получиться из разных сеток прямых: на рисунке 2 изображена так называемая целочисленная решетка, т.е. множество точек, имеющих в декартовой (прямоугольной) системе координат целочисленные координаты. Целочисленную решетку вместе с сеткой прямых можно представлять себе как бесконечный лист клетчатой бумаги (тогда основным параллелограммом будет квадрат со стороной 1). Ту же самую целочисленную решетку можно получить, проводя пунктирные прямые (тогда основным параллелограммом служит параллелограмм ABCD). Таким образом, понятие основного параллелограмма решетки связано не только с самой решеткой, но и с сеткой прямых, составляющих эту решетку. Важное свойство решеток отражает следующая задача: В некотором узле A решетки находится охотник, а в остальных зайцы (рис.3,а). Охотник наугад стреляет (траекторией пули будет являться луч с вершиной в A). Вернется ли он домой с добычей? Теорема. Пусть множество М на плоскости обладает следующими свойствами: 1) расстояние между любыми двумя точками не меньше некоторого положительного числа d; 2) если три точки A,B,C множества М являются вершинами некоторого параллелограмма ABCD, то и четвертая вершина D этого параллелограмма принадлежит множеству М. Тогда М – решетка. Доказательство. Возьмем произвольную точку В, принадлежащую множеству М. Пусть А – ближайшая к В точка из М (такая точка существует, так как все попарные множества М больше d). 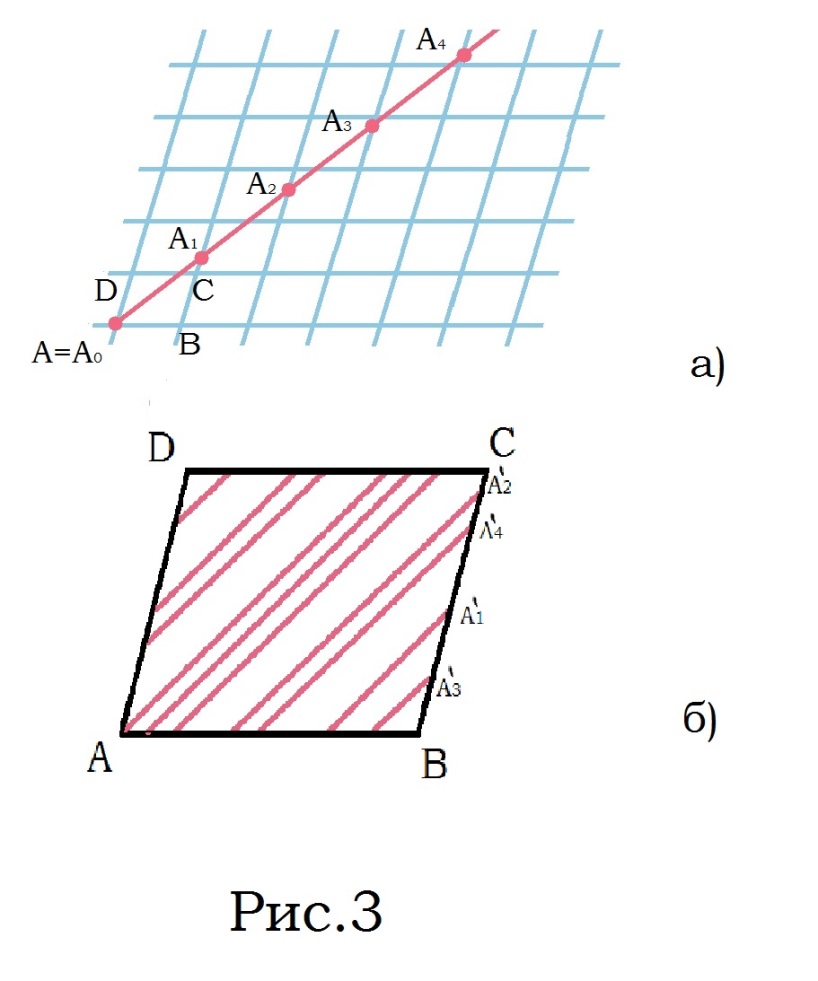 Через точки А и В проведем прямую. Среди точек множества М, не лежащих на этой прямой, выберем ближайшую к точке В – точку С – и построим параллелограмм АВСD. В силу второго свойства точка В также принадлежит множеству М. 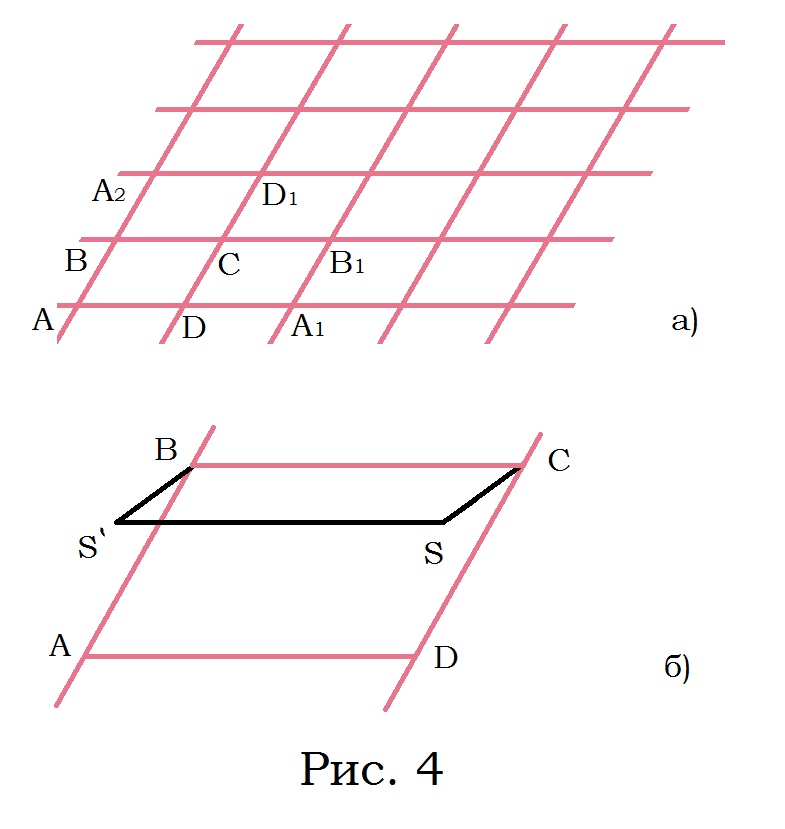 Построим решетку, порождаемую параллелограммом АВСD. Докажем, что множество М. Из второго свойства следует, что все узлы этой решетки принадлежат множеству М. Осталось проверить, что ни на границе, ни внутри параллелограмма АВСD нет точек множества М, отличных от его вершин. Если какая-то точка S лежит внутри параллелограмма (рис.4,б), то хотя бы один из углов ASB, BSC, CSD и ASD будет тупым или прямым. Поэтому расстояние от S до одной из его вершин окажется меньше какой-нибудь стороны (если S лежит на границе – то же самое); пусть, например, это расстояние SC. Построим параллелограмм BCSS` (S` принадлежит М). Тогда BS` меньше либо ВС, либо ВА, что противоречит выбору точки С, либо точки А. Аналогично доказываются и остальные случаи. Теорема доказана. 1.2. Правильные многоугольникиВ 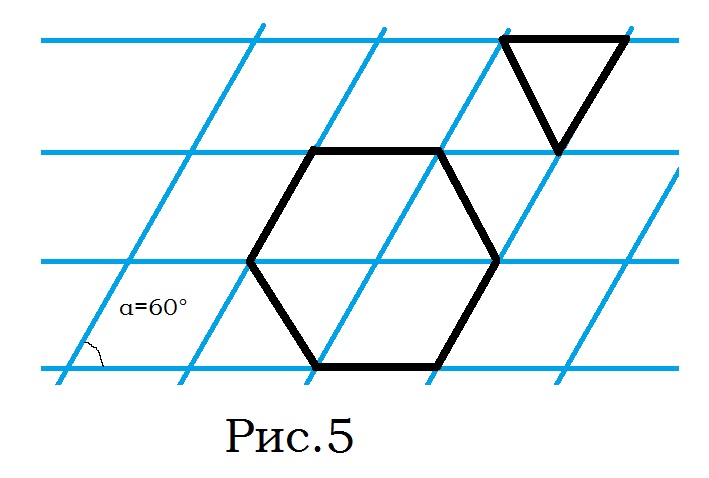 озьмем лист клетчатой бумаги. Понятно, что квадрат с вершинами в узлах такой решетки можно нарисовать многими способами. А можно ли на клетчатой бумаге нарисовать, например, правильный треугольник? Очевидно, что нет, ведь тангенс угла правильного треугольника равен озьмем лист клетчатой бумаги. Понятно, что квадрат с вершинами в узлах такой решетки можно нарисовать многими способами. А можно ли на клетчатой бумаге нарисовать, например, правильный треугольник? Очевидно, что нет, ведь тангенс угла правильного треугольника равен  – нерациональное число. Но, с другой стороны, не трудно построить решетку, на которую можно поместить правильный треугольник (рис. 5). – нерациональное число. Но, с другой стороны, не трудно построить решетку, на которую можно поместить правильный треугольник (рис. 5). Но что же с остальными многоугольниками? Существуют, например, решетка, на которую можно поместить правильный пятиугольник так, чтобы все его вершины оказались узлами этой решетки? Оказывается, что такой решетки нет. Предположим, что нам удалось построить решетку так, чтобы вершины правильного пятиугольника оказались в ее узлах (рис. 6).  Проведем диагонали этого пятиугольника. По лемме 2 точки пересечения диагоналей являются узлами решетки: каждая из них служит четвертой вершиной параллелограмма, три другие вершины которого – узлы решетки (точка А1, например, - вершина параллелограмма А1CDE). Эти точки образуют правильный пятиугольник со стороной в  раз большей стороны исходного пятиугольника. Проведя диагонали нового пятиугольника, получим еще меньший пятиугольник с вершинами в узлах нашей решетки и так далее. В конце концов сторона пятиугольника станет меньше минимального расстояния между узлами решетки. Значит, мы не сумеем придумать такую решетку, в которую можно было бы поместить правильный пятиугольник. раз большей стороны исходного пятиугольника. Проведя диагонали нового пятиугольника, получим еще меньший пятиугольник с вершинами в узлах нашей решетки и так далее. В конце концов сторона пятиугольника станет меньше минимального расстояния между узлами решетки. Значит, мы не сумеем придумать такую решетку, в которую можно было бы поместить правильный пятиугольник.Докажем, что то же самое происходит со всеми остальными правильными q-угольниками при q ≥ 7. Доказательство очень схоже с предыдущим. Предположим, что правильный многоугольник с вершинами в узлах существует, и построим меньший q-угольник с вершинами в узлах. В итоге вновь получим противоречие. Поэтому нужно лишь указать, как из данного правильному q-угольника с вершинами в узлах решетки построить меньший правильный q-угольник, вершины которого будут находиться в узлах нашей решетки. Пусть А1, А2, … Аq – узлы некоторой решетки, являющиеся вершинами правильного q-угольника  , и пусть М – произвольный узел решетки (рис.7). Отложим от точки М отрезки MА`1, МА`2, МА`3, …, MА`q, равные параллельные и так же направленные, как сторона АqА1, А1А2, А2А3, …, Аq-1Аq нашего многоугольника. Точки А`1, А`2, А`3,…, А`q – узлы решетки, так как каждая из них является четвертой вершиной параллелограмма, три другие вершины которого – узлы. Легко видеть, что многоугольник А`1, А`2, А`3,…, А`q – правильный, а длина его стороны в kq = , и пусть М – произвольный узел решетки (рис.7). Отложим от точки М отрезки MА`1, МА`2, МА`3, …, MА`q, равные параллельные и так же направленные, как сторона АqА1, А1А2, А2А3, …, Аq-1Аq нашего многоугольника. Точки А`1, А`2, А`3,…, А`q – узлы решетки, так как каждая из них является четвертой вершиной параллелограмма, три другие вершины которого – узлы. Легко видеть, что многоугольник А`1, А`2, А`3,…, А`q – правильный, а длина его стороны в kq =  раз больше длины стороны исходного q-угольника. раз больше длины стороны исходного q-угольника.Таким образом, мы доказали, что многоугольниками, помещающимися на точечных решетках, могут быть только квадраты, правильные треугольники и правильные шестиугольники. 1.3. Формула Пика.Теперь перейдем к самой формуле Пика. Формула пика гласит, что площадь многоугольника с целочисленными вершинами равна  , где В — количество целочисленных точек внутри многоугольника, а Г — количество целочисленных точек на границе многоугольника. , где В — количество целочисленных точек внутри многоугольника, а Г — количество целочисленных точек на границе многоугольника.Докажем эту формулу. Для начала, затем что формула Пика верна для квадрата со стороной 1. В таком случае количество узлов внутри равно нулю, на границах количество узлов равно 4, а площадь равна одному. Подставив в формулу, мы убедимся все верно  . .Теперь рассмотрим прямоугольник, стороны которого лежат на линиях решетки. Длины его сторон обозначим как X и Y. Тогда количество узлов внутри прямоугольника будет равно  , а количество узлов на его сторонах будет равно , а количество узлов на его сторонах будет равно 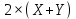 . Из курса геометрии мы знаем, что площадь нашего прямоугольника будет равна XY, но чему же будет равна площадь по формуле Пика? . Из курса геометрии мы знаем, что площадь нашего прямоугольника будет равна XY, но чему же будет равна площадь по формуле Пика? 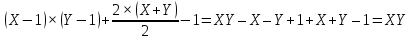 . То есть формула Пика оказалась верной и для любого прямоугольника. . То есть формула Пика оказалась верной и для любого прямоугольника.Далее рассмотрим прямоугольный треугольник, который можно получить из уже рассмотренного нами прямоугольника проведением в нем диагонали. Пусть на диагонали этого треугольника лежит Z узлов решетки. Тогда в этом случае количество точек внутри будет равно: 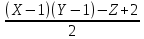 , а количество точек на границах будет равно: , а количество точек на границах будет равно: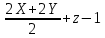 . Подставив это в формулу, мы получим, что площадь равна . Подставив это в формулу, мы получим, что площадь равна 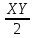 . Очевидно, что формула Пика оказалась верна для прямоугольного треугольника. . Очевидно, что формула Пика оказалась верна для прямоугольного треугольника.Любой остроугольный треугольник можно получить отрезанием от прямоугольника прямоугольных треугольников, а любой тупоугольный, можно получить отрезанием от прямоугольника не только нескольких прямоугольных треугольников, но и прямоугольника поменьше. И если для любого прямоугольника и прямоугольного треугольника эта формула верна, то она верна и для любого треугольника. Осталось перейти от треугольников к многоугольникам. Так как любой многоугольник можно разбить на треугольники, по крайней мере, диагоналями, нам осталось доказать, что при добавлении любого треугольника к произвольному многоугольнику формула Пика остается верной. Пусть многоугольник и треугольник имеют общую сторону. Предположим, что формула Пика справедлива для данного многоугольника (М), и докажем, что она останется справедлива и при добавлении к нему треугольника (Т). Так как треугольник и многоугольник имеют общую сторону, то все целочисленные точки, принадлежащие этой стороне, кроме двух вершин, становятся внутренними точками нового многоугольника (нМ). Вершины же будут точками границ. Обозначим число общих точек за а, тогда: 1) число внутренних целочисленных точек многоугольника будет равно 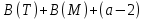 2) число точек границ нового многоугольника будет равно 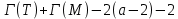 , где В- количество точек внутри фигуры, Г- количество точек на границе фигуры. Отсюда получаем, что , где В- количество точек внутри фигуры, Г- количество точек на границе фигуры. Отсюда получаем, что 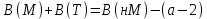 и и 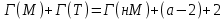 . А из нашего предположения, что теорема верна отдельно и для многоугольника и треугольника, следует: . А из нашего предположения, что теорема верна отдельно и для многоугольника и треугольника, следует: 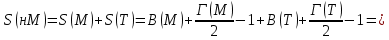 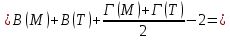 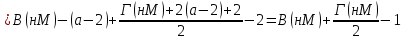 Таким образом, мы доказали теорему Пика для любого многоугольника. Но можно ли посчитать количество узлов как-то иначе? 1.4. Подсчет узлов на отрезке с вершинами в узлах сетки.Обозначим произвольные узлы сетки за M и L. Пусть первый узел, встречающийся на отрезке ML это узел P1. Тогда построим прямоугольный треугольник MP1T1. Если точка P1 не совпадает с L, то сместим треугольник MP1T1 вдоль по оси ML на расстояние MP1. Мы получили равный ему треугольник P1P2T2, следовательно, P2 будет являться узлом и между P1 и P2 не будет ни одного узла. Очевидно, что после нескольких таких смещений точка Pn совпадет с L. Теперь рассмотрим треугольник MNL: MN=n×MT1, NL=n×T1P1, ML=n×MP1. Таким образом, вы можем узнать, сколько узлов лежит между двумя узлами сетки.  Положим, что в треугольнике MLN MN=r, а LN=s, тогда существует следующая теорема: Если r и s взаимно просты, то между А и В на отрезке АВ нет узлов сетки. Если же наибольший общий делитель r и s равен d, где d > 1, то на отрезке АВ между точками А и В расположены ровно (d – 1) узлов сетки. Докажем эту теорему: пусть числа r и s взаимно просты, тогда НОД(r;s)=1 Если между А и В были n узлов (n ≥ 1), то, взяв ближайший к А узел С, мы получим, что r = n×MT1, s = n×T1P1, то есть r и s имеют общий делитель n, больший 1. Но мы предположили, что они взаимно просты, следовательно, получили противоречие. Теперь предположим, что НОД(r;s)=d >1. Тогда, разделив отрезки MN и NL на d равных частей, вернемся к нашему рисунку. В таком случае, между точками M и L расположено не более чем (d-1) узлов, иначе между M и P1 были бы и другие узлы. Пусть P`1 – ближайший к M узел. В таком случае MP` < MP ,следовательно ML/MP`1 – целое число k, большее d (поскольку ML/MP=d ). Но r = MN = k×MT`1 , s = NL = k×P`1T`1 , где k = ML/MP`1, но тогда НОД(r;s)=k. Опять получили противоречие, а значит наше предположение неверно и теорема доказана. После всей теоретической части я бы хотел еще разобрать задачу, которую я встретил при поиске олимпиадных задач на формулу Пика. Условие задачи состоит в следующем: шахматный король обошел доску 8 на 8 клеток, побывав на каждом поле ровно один раз и последним ходом вернувшись на исходное поле. Ломанная, соединяющая последовательно центры полей, которые проходил король, не имеет самопересечений. Какую площадь может иметь эта ломаная? Какую наибольшую длину она может иметь? Из формулы Пика следует, что площадь, ограниченная ломаной, равна 64/2-1=31 (узлами сетки будут служить 64 центра полей, а по условию они все лежат на границе многоугольника). Теперь ответим на второй вопрос задачи. Приведем пример пути, в котором 36 из 64 ходов имеют длину  . . Докажем, что больше таких ходов быть не может. На каждом отрезке длинною  , входящем в путь короля, построим, как на диагонали, квадрат 1 на 1. Одна половина этого квадрата лежит вне многоугольника, который ограничивает путь короля. Но общая площадь, занятая такими половинками, не превышает 49-31=18 поскольку все они не выходят за пределы квадрата 7 на 7 клетчатой бумаги. Значит, количество диагональных ходов не превышает 36. Следовательно, ответом на второй вопрос будет являться , входящем в путь короля, построим, как на диагонали, квадрат 1 на 1. Одна половина этого квадрата лежит вне многоугольника, который ограничивает путь короля. Но общая площадь, занятая такими половинками, не превышает 49-31=18 поскольку все они не выходят за пределы квадрата 7 на 7 клетчатой бумаги. Значит, количество диагональных ходов не превышает 36. Следовательно, ответом на второй вопрос будет являться  Вывод.Подводя итог моей работы, могу сказать, что выбранная тема оказалась куда более объемной, чем я предполагал. На основе изученного мною материала я создал сайт, который, надеюсь, поможет и другим разобраться в этой, как оказалось, не простой теме. По мере исследования теоретических материалов по математике я решал ряд практических задач из этой области, изучил новые приемы по работе на языке HTML, а также освоил графический редактор. В ходе изучения формулы Пика я коснулся и других тем. К сожалению, я не успел подробно разобраться в таких аспектах как, например, триангуляция многоугольника. Поэтому я рассчитываю продолжить изучение данной темы и в следующем полугодии, вместе с этим совершенствуя и свой сайт. Список литературы.https://ru.wikipedia.org/wiki/Формула_Пика http://hijos.ru/2011/09/14/formula-pika/ http://pandia.ru/text/78/382/600.php Журнал «Квант» 1974 год №12. Геометрия на клетчатой бумаге. Малый МЕХмат МГУ. Жарковская Н. М., Рисс Е. А. Геометрия клетчатой бумаги. Формула Пика // Математика, 2009, № 17, с. 24-25. В.В.Вавилов, А.В.Устинов .Многоугольники на решетках.М.МЦНМО,2006. Задачи открытого банка заданий по математике ФИПИ, 2010 – 2015 |
