Балочная клетка. Балочная клетка Тольятти. Балочная клетка нормального типа

• Название: Балочная клетка нормального типа
• Анкор: Балочная клетка
• Дата: 13.10.2021
• Размер: 351.23 Kb.
• Имя файла: Балочная клетка Тольятти.docx
• Тип: Курсовая; #246732
• страница: 4 из 10

3. Расчет и конструирование главной балки

3.1 Определение нагрузок и расчетных усилий.

Интенсивность расчетной погонной нагрузки находим по формуле:

q_гл.б = q_вт.б·ℓ_вт.б/а = 19,49·5,0/1,0 = 97,45 кН/м.

Интенсивность нормативной погонной нагрузки определяем по формуле:

q_гл.б^н = q_вт.б^н·ℓ_вт.б/а = 16,33·5,0/1,0 = 81,65 кН/м.

Расчетные значения изгибающего момента и поперечной силы определяем по формулам:

М 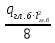=1,04· = 1,04·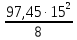 = 2850,4 кН·м.

Q_max = 1,02· 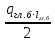= = 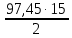730,9 кН.

Расчетная схема главной балки приведена на рисунке 4.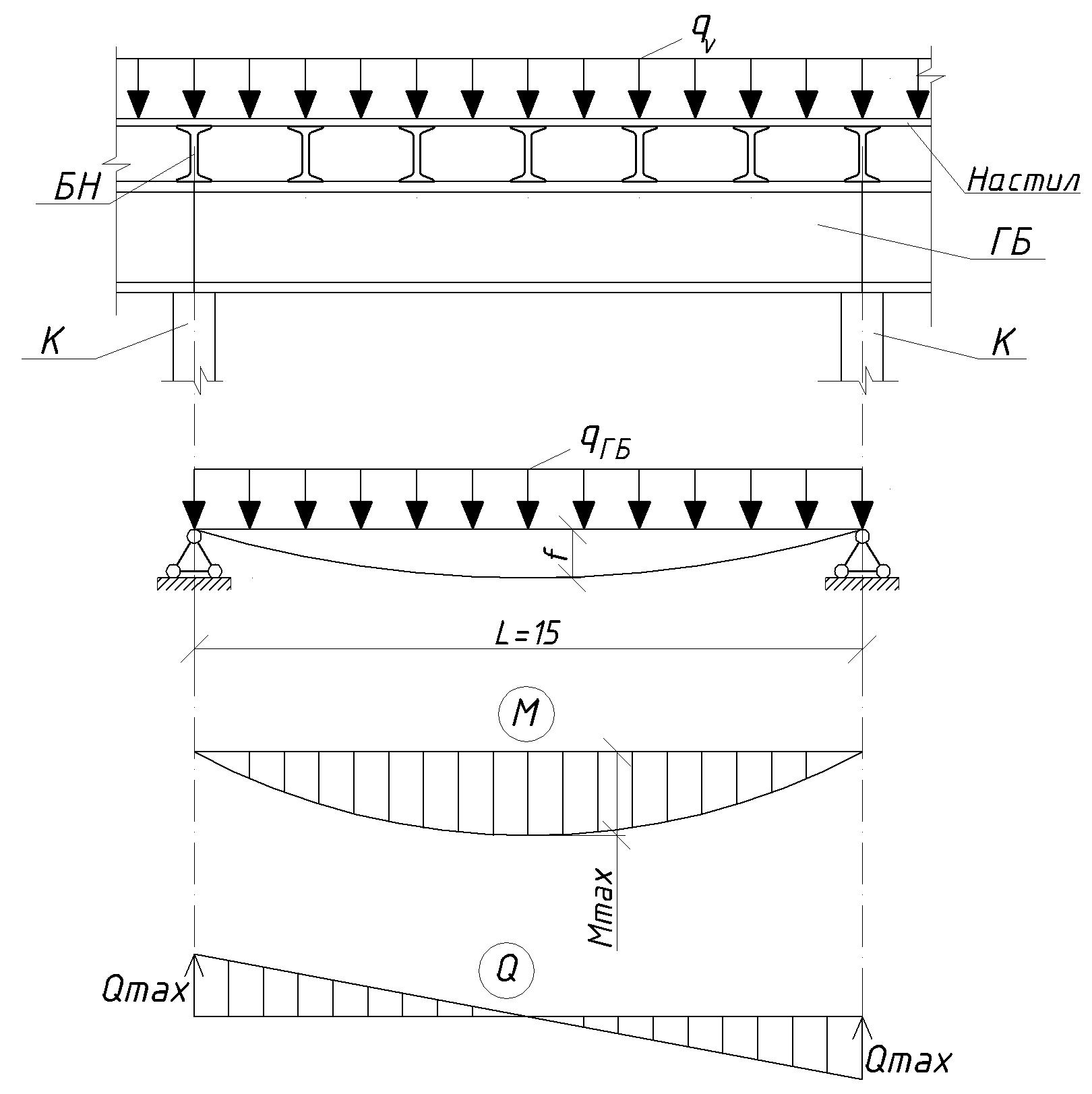



Рис. 4 – Расчетная схема главной балки

3.2 Подбор и проверка сечения

Для главной балки класс стали по заданию – С245 (R_y = 240 МПа при t = 4 ÷ 20 мм).

Подбор сечения состоит в определении размеров поясов и стенки балки на основе заданных технологическим заданием условий, экономичности, прочности, устойчивости, жесткости и технологичности изготовления.

Требуемый момент сопротивления сечения балки определяем по упругой стадии по формуле: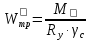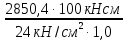

= = 11877 см³,

где: R_y = 24 кН/см² – расчетное сопротивление стали класса С245 на сжатие, растяжение и изгиб по пределу текучести;

γ_с = 1,0 – коэффициент условий работы принятый по табл. 1 [5].

Минимальная высота балки определяется жесткостью балки – ее предельным прогибом 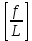= 1/400. Минимальную высоту рассчитываем по формуле:

h_min = ,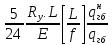

где: 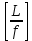= 400 – величина обратная предельно допускаемому прогибу [4]; Е – модуль упругих деформаций.

h_min = 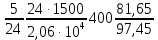= 121,8 см ≈ 122 см.

Ориентировочно толщину стенки t_ω определяем по формуле:

t_ω = 7+3·ℓ_гб·10^-4 = 7+3·15000·10^-4 = 11,5 мм.

Примем t_ω = 12 мм.

Оптимальная высота балки диктуется экономическими соображениями.

Оптимальную высоту сечения балки рассчитываем по формуле:

h_oпт = k ,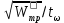

где: k – коэффициент зависящий от конструктивного оформления балки; для сварных балок k = 1,15-1,2; t_ω – толщина стенки балки.

Подставляя t_ω = 1,2 см, коэффициент k = 1,15 и 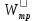= 11877 см³ определяем оптимальную высоту балки:

h_опт = 1,15 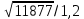= 114,4 см.

Принимаем высоту балки h_ГБ = 130 см > h_min.

Предварительно примем толщину пояса t_f = 20 мм и найдем толщину стенки из условия среза на опоре при h_ef = h_гб - 2t_f = 130 - 2·2 = 126 см

С позиции среза требуемая толщина стенки определяется как:

t_ω ≥ 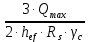= = 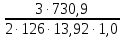0,63 см < t_ω = 1,2 см.

где: R_S – расчетное сопротивление стали срезу.

В соответствии с табл. 2 [5] R_S = 0,58R_y = 0,58·24 = 13,92 кН/см².

Предварительно принятая толщина стенки по условиям среза достаточна.

Проверяем условие обеспечения местной устойчивости стенки при отсутствии продольного ребра жесткости:

t_ω ≥ 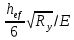= = 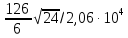0,72 см < t_ω = 1,2 см.

Требуемый момент инерции сечения балки

I_тр = 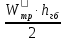= = 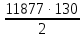772005 см⁴.

Определяем момент инерции стенки балки по формуле:

I_w = 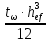= = 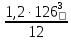200038 см⁴.

Требуемая площадь сечения пояса

А_f = 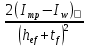= = 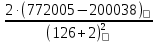69,82 см².

Ширина пояса

b_f = А_f/t_f = 69,82/2 = 34,91 см, что меньше 1/3 h = 43 см.

Ширину поясов принимают равной 1/3÷1/5 высоты балки для обеспечения ее общей устойчивости и равномерного распределения продольных напряжений по ширине листа. Значения b_f должны быть в пределах 43÷26 см, найденная ширина пояса находится в этих пределах. В соответствии с ГОСТ 82-70^* принимаем окончательно ширину пояса b_f= 360 мм, т.е. пояс – 360х20 мм.

Проверим условие обеспечения местной устойчивости для принятого сечения пояса:

b_ef = (b – t_w)/2 = (36 – 1,2)/2 = 17,4 см

b_ef/t_f = 17,4/2,0 = 8,7 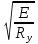< 0,5· = 0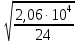,5· = 14,65.

Условие выполняется.

Проверим принятое сечение на прочность по нормальным напряжениям:

σ = 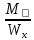≤ R_y·γ_c,

Определяем момент инерции сечения балки:

I_x = 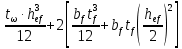= = 789910 см⁴.

Момент сопротивления сечения балки:

W_x = 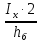= = 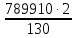12152,5 см³.

Проверяем несущую способность балки по упругой стадии ее работы:

σ = 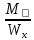= = 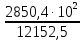23,5 кН/см²,

что меньше R_y·γ_c= 24 кН/см²; недонапряжение составляет 2,1%, т.е. находится в пределах допустимых 5%.