Балочная клетка. Балочная клетка Тольятти. Балочная клетка нормального типа
 Скачать 351.23 Kb. Скачать 351.23 Kb.
|
3.5 Конструирование и расчет опорной части главной балкиКонструкцию опорной части главной балки принимаем с опорным ребром в торце балки. Нижний торец опорного ребра должен быть простроган. Толщину ребра принимаем tр = 20 мм. Выпуск ребра за нижнюю полку примем равным а1 = 20 мм, что меньше 1,5tр. В этом случае в соответствии с п. 7.12 [5] расчет ребра следует вести из условия работы на смятие. Отсюда, определяем требуемую ширину торца ребра из условия предотвращения смятия при действии нагрузки равной реакции главной балки Qmax: bртр = 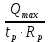 , ,где расчетное сопротивление смятию торцевой поверхности Rр = Rи в соответствии с табл. 2 [5]. Для стали класса С245 расчетное сопротивление на сжатие, растяжение, изгиб, определенное по временному сопротивлению, равно Rи = 36 кН/см2 табл. В.5 [5]. Определяем требуемую ширину опорного ребра: bртр = 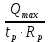 = =  = 17,1 см. = 17,1 см.В соответствии с ГОСТ 82-70*принимаем bр = 200 мм. Опорную часть балки составного сечения следует рассчитывать на продольный изгиб из плоскости как стойку, нагруженную опорной реакцией. В расчетное сечение стойки следует включать ребро и полосу стенки шириной lω, определенную по формуле: lω = 0,65tω 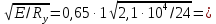 19,22 см. 19,22 см.Расчетную высоту стойки следует принимать равной высоте стенки hω = 144 см. Проверку устойчивости стойки следует проводить из условия: σ = Qmax/φуА≤ Ry·γc, где А - площадь сечения стойки. Определяем геометрические характеристики сечения стойки: площадь сечения А = tpbp + 0,65tω2 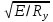 , ,А = 2·20 + 0,65· 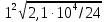 = 59,23 см2; = 59,23 см2;момент инерции сечения относительно оси «у» Iy = tpbp3/12 + lωtω3/12 = 2·203/12 + 19,22·13/12 = 1334,9 см4; радиус инерции сечения относительно оси «у» iy = 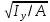 = = 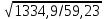 = 4,75 см. = 4,75 см.Гибкость стойки в плоскости перпендикулярной оси «у» будет равна: λу = hω/iy = 144/4,75 = 30,3  Коэффициент продольного изгиба φу = 0,901 определяем в соответствии с табл. Д.1 [5] для сечения типа «с» в зависимости от условной гибкости стойки λ = λу Коэффициент продольного изгиба φу = 0,901 определяем в соответствии с табл. Д.1 [5] для сечения типа «с» в зависимости от условной гибкости стойки λ = λу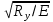 = 30,3 = 30,3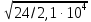 = 1,02. = 1,02.Проверяем устойчивость: σ = 1228,7/0,901·59,23 = 23,02 кН/см2, что меньше Ryγc = 24 кН/см2 Устойчивость стенки обеспечена. Принимаем опорное ребро из листа широкополосной универсальной стали сечением – 200х20 мм. 3.6 Проверка местной устойчивости главной балкиВ балках потерять устойчивость могут сжатый пояс от действия нормальных напряжений и стенка от действия касательных или нормальных напряжений. Визуально это будет проявляться в виде местных изгибных деформаций: выпучин, складок, волн. Потеря устойчивости одним из элементов балки полностью или частично выводит его из работы, рабочее сечение балки уменьшается, часто становится несимметричным, цент изгиба смещается, что может привести к преждевременной потере несущей способности всей балки. Проверка местной устойчивости стенки от действия касательных напряжений. Вблизи опоры стенка балки подвергается воздействию значительных касательных напряжений. При их достижении, т.е. τ ≥ τcr, стенка может выпучиться, образуя волны, наклоненные к оси балки под углом около 45°. Величина критических напряжений зависит от условной гибкости стенки λω = (hω/tω) 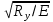 . .В соответствии с [п.8.5.9, 5] для исключения потери устойчивости стенки от действия касательных напряжений необходима постановка ребер жесткости: при отсутствии подвижной нагрузки, если гибкость стенки λω превышает 3,2; при наличии подвижной нагрузки, если гибкость стенки λω превышает 2,2. Расстояние между основными ребрами жесткости не должно превышать 2hω при > 3,2. Ребра жесткости располагают чаще к опорам, по возможности под балками настила, симметрично относительно пролета.  В рассматриваемом случае λω = (hω/tω) В рассматриваемом случае λω = (hω/tω) 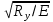 = 144/1· = 144/1·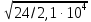 = 4,87 > 3,2. Отсюда максимальное расстояние между ребрами 2hω = 2·144 = 288 см. = 4,87 > 3,2. Отсюда максимальное расстояние между ребрами 2hω = 2·144 = 288 см.Принимаем расстояние между рёбрами жесткости, а = 200 см (кратно шагу балок настила 100 см) по всему пролету балки за исключением двух опорных отсеков. Потеря устойчивости стенки от действия нормальных напряжений. Максимальные нормальные напряжения в случае равномерно распределенной нагрузки имеют место в середине пролета, сжатая зона располагается выше нейтральной оси. Здесь вероятна потеря устойчивости стенки, появление выпучины. Исключить появление выпучины можно двумя способами: принятием достаточной толщины стенки или постановкой продольных ребер жесткости. Постановка ребер эффективна при высоте главной балки hгб > 2,0 м. В рассматриваемом случае hгб < 2,0 м, значит, устойчивость стенки от действия σ следует обеспечить путем принятия достаточной толщины: tω = hгб/5,5· 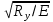 = 150/5,5· = 150/5,5·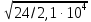 = 0,92 см. = 0,92 см.При компоновке сечения принята толщина tω = 10 мм, что больше, чем требуемая с позиции обеспечения местной устойчивости стенки. Потеря устойчивости полки от действия нормальных напряжений Сжатая полка – это длинная пластина, шарнирно прикрепленная к стенке балки и нагруженная равномерно распределенным по сечению нормальным напряжением. При достижении критических значений σfcr наступает потеря устойчивости полки: происходит волнообразное выпучивание ее свободного края.  Устойчивость полки зависит от условной гибкости ее свеса λf и характера закрепления. Условная гибкость свеса определяется как Устойчивость полки зависит от условной гибкости ее свеса λf и характера закрепления. Условная гибкость свеса определяется какλf = bef/tf· 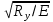 , ,где bef и tf – соответственно свес и толщина полки. Величина свеса полки принимается равной: bef = (bf - tω)/2, где tω – толщина стенки балки. Балка имеет поперечные ребра жесткости, которые увеличивают устойчивость сжатой полки, являясь ее окаймлением. В соответствии с [п.7.24, 5] для обеспечения устойчивости пояса необходимо, чтобы величина условной гибкости полки находилась в пределах ее предельно допустимой величины: λf ≤ λиf. Для полок, имеющих окаймление, предельно допустимая величина условной гибкости определяется как λиf = 0,75 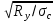 , ,где 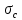 – напряжение в полке в середине пролета; в рассматриваемом случае σс = 22,96 кН/см2. – напряжение в полке в середине пролета; в рассматриваемом случае σс = 22,96 кН/см2.Проверка устойчивости. Определяем свес полки: bef = (38 – 1)/2 = 18,5 см. Условная гибкость свеса λf = bef/tf· 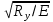 = 18,5/3· = 18,5/3·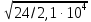 = 0,21. = 0,21.Предельно допустимая условная гибкость равняется: λиf = 0,75 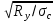 = 0,75· = 0,75·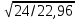 = 0,767. = 0,767.Таким образом устойчивость пояса обеспечена: 0,21 < 0,767. Потеря устойчивости стенки от совместного действия нормальных, касательных и местных напряжений. На совместное действие напряжений проверим устойчивость стенки во втором, наиболее напряженном отсеке от опоры, под балкой настила на расстоянии х1 = 3,0 м. В соответствии с п. 8.5.3 [5] устойчивость стенок балок 1-го класса симметричного сечения, укрепленных только поперечными ребрами жесткости, при наличии местного напряжения (σlос ≠ 0) и при условной гибкости λω ≤ 6 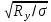 следует считать обеспеченной, если выполняется условие [формула (80), 5]: следует считать обеспеченной, если выполняется условие [формула (80), 5]: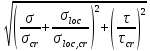 ≤ γc ≤ γcДействительная условная гибкость стенки λω = 4,87, что меньше 6 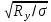 = 6· = 6·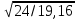 = 6,72. = 6,72.Числители дробей (σ, σloc, τ) зависят от нагрузки и, следовательно, от действующих усилий. В частности, σ и τ – соответственно от изгибающего момента и перерезывающей силы. Определяем изгибающий момент и перерезывающую силу в сечении, расположенном на расстоянии х1 = 3,0 м от оси по формулам: Мх1 = 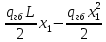 = = 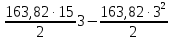 = 2948,76 кНм; = 2948,76 кНм;Qx1 = 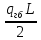 - - 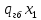 = = 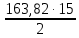 - - 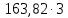 = 737,2 кН. = 737,2 кН.В соответствии с п. 8.5.2 [5] проверку устойчивости стенок балок 1-го класса следует выполнять с учетом наибольшего сжимающего напряжения σ у расчетной границы стенки принимаемого со знаком «плюс», среднего касательного напряжения τ и местного напряжения σloc в стенке под сосредоточенной нагрузкой. Напряжения σ и τ следует вычислять по формулам: σ = 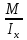 y, τ = y, τ =  . .В рассматриваемом случае М = Мх1 и Q =Qx1 – изгибающий момент и перерезывающая сила в сечении х1; Ix – момент инерции основного сечения; t и h – соответственно толщина и высота стенки, т.е. t = tω и h = hω; у = hω/2. Определяем нормальные и касательные напряжения: σ = 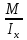 y = y = 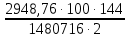 = 14,34 кН/см2; = 14,34 кН/см2;τ =  = = 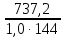 = 5,12 кН/см2. = 5,12 кН/см2.Местные напряжения принимаем равными σloc = 8,23 кН/см2 из расчета стенки на местное давление. Критические напряжения (σcr, σloc,cr, τcr) зависят от гибкости, прочности стенки (отсека, пластинки), характера закрепления. В данном случае пластинка (отсек) представляет собой часть стенки размерами 200х144 см, закрепленную между поясами и поперечными ребрами. Определяем напряжения в соответствии с требованиями [п.8.5.3, 5]. Критические касательные напряжения определяем по формуле (83): τcr = 10,3 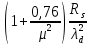 , ,где μ – отношение большей стороны пластинки к меньшей; Rs – расчётное сопротивление срезу; λd = d/tω 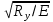 где d – меньшая из сторон пластинки. где d – меньшая из сторон пластинки.В рассматриваемом варианте d = 144 см, отсюда: μ = 200/144 = 1,39; λef = 144/1 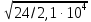 = 4,87 = 4,87Определяем τcr = 10,3·(1+0,76/1,392) 13,92/4,872 = 8,42 кН/см2. Особенности определения критических нормальных напряжений зависят от отношения сторон отсека, а/hω и наличия местных напряжений σloc. В нашем случае а/hω = 200/144 = 1,39, что больше 0,8, а местные напряжения σloc не равны нулю. Отсюда в соответствии с п. 8.5.5,б проверку устойчивости стенки по формуле (80) [5] следует выполнять дважды: при значении σcr, вычисленном по формуле (81) [5] с учетом требований п. 8.5.4, и при таком значении σloc,cr (формула 82 [5]), когда при определении коэффициентов с1 и с2 вместо размера а принят а1 = 0,5а при 0,8 ≤ а/hω ≤ 1,33 или а1 = 0,67hω при а/hω > 1,33; при значениях σcr и σloc,cr, вычисленных при фактическом значении а/hω (если а/hω > 2, в расчете следует принимать а/hω = 2); при этом коэффициент сcr в формуле (81) следует определять по таблице 16. Определение нормальных критических напряжений для первой проверки. Критические нормальные напряжения σcr определяем по формуле (81) [5]: σcr = 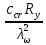 , ,где коэффициент сcr в соответствии с п. п. 8.5.4 – 8.5.6 следует определять по таблице 12 [5] в зависимости от отношения сторон отсека а/hω и наличия местных напряжений σloc. В рассматриваемом случае σloc отсутствуют, а/hω = 1,39. Отсюда, так как а/hω > 0,8, коэффициент сcr определяется в соответствии с п. 8.5.6, б [5] по табл. 12 в зависимости от отношения а/hω и величины коэффициента δ. Коэффициент δ следует определять по формуле (84) [5] как δ = β 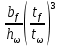 , ,где: bf и tf – ширина и толщина полки; hω и tω – высота и толщина стенки; коэффициент β определяется по табл. 13 [5] в зависимости от вида балок и условий работы сжатого пояса; в рассматриваемом случае β = 0,8 (для прочих балок в прочих случаях). Определяем коэффициент δ: δ = 0,8 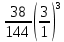 = 5,7. = 5,7.По табл. 12 определяем коэффициент сcr = 34,77 в зависимости от вида поясных соединений балки (сварные) и значения коэффициента δ = 5,7. Таким образом, нормальные критические напряжения будут равны: σcr = 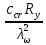 = = 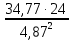 = 35,19 кН/см2. = 35,19 кН/см2.Критические местные нормальные напряжения σloc,cr определяем по формуле (82) [5]: σloc,cr = 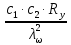 , ,где с1 и с2 – коэффициенты, определяемые согласно [п. 8.5,5]: с1 по табл. 14 в зависимости от отношения а/hω и значения коэффициента ρ определяемого в соответствии с п. 8.5.5 [5], ρ = 1,04lef/hef ; (здесь значение lef следует определять согласно требованиям 8.2.2 [5]; с2 по табл. 15 в зависимости от отношения а/hω и значения коэффициента δ. Определяем коэффициент с1. В соответствии с п. 8.2.2 [5] lef – условная длина распределения нагрузки от балки настила на стенку главной балки; она определяется по формуле: lef = 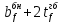 , ,где: bfбн – ширина пояса балки настила; tfгб – толщина верхнего пояса главной балки. В нашем случае bfбн = 13,5 см (I 30), tfгб = 3,0 см. Отсюда lef = 13,5 + 2·3 = 19,5 см. Определяем коэффициент ρ = 1,04lef/hef = 1,04·19,5/144 = 0,141. В соответствии с п. 8.5.5, б [5], так как отношение сторон отсека а/hω = 200/144 = 1,39, то есть больше 1,33, в отношение а/hω подставляем а = 0,67hω; таким образом, получаем, а/hω = 0,67. По табл. 14 [5] определяем коэффициент с1 = 30,68 в зависимости от значений ρ = 0,141 и а/hω = 0,67. Определяем коэффициент с2 по табл. 15 [5]. Отношение а/hω = 0,67, δ = 5,7; отсюда с2 = 1,697. Определяем σloc,cr = 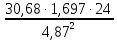 = 52,68 кН/см2. = 52,68 кН/см2.Производим 1-ю проверку устойчивости стенки: 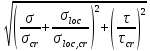 = = 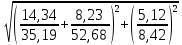 = 0,83 < γс = 1,0 = 0,83 < γс = 1,0Следовательно, устойчивость стенки обеспечена. Определение нормальных критических напряжений для второй проверки Критические нормальные напряжения σcr определяем по формуле (81) [5], в которой сcr определяется по табл. 16 [5] в зависимости от а/hω: σcr = 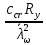 , ,В данном случае сcr = 52,42 , так как а/hω = 200/144 = 1,39. σcr = 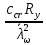 = = 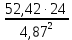 = 53,05 кН/см2. = 53,05 кН/см2.Критические местные нормальные напряжения σloc,cr определяем по формуле (82) [5]: σloc,cr = 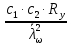 . .По а/hω = 1,39, ρ = 0,141 и δ = 5,7 коэффициенты с1 и с2 принимаем соответственно по табл. 14 и 15: с1 = 15,88 с2 = 2,18. Таким образом, критические местные нормальные напряжения будут равны: σloc,cr = 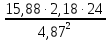 = 35,03 кН/см2. = 35,03 кН/см2.Производим 2-ю проверку устойчивости стенки: 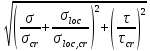 = = 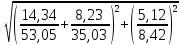 = 0,79 < γс = 1,0. = 0,79 < γс = 1,0.Устойчивость стенки обеспечена. Обе проверки местной устойчивости стенки удовлетворяются. Жесткость стенки обеспечена. |
