Барасюк Я. М
 Скачать 3.63 Mb. Скачать 3.63 Mb.
|
5.2.3. Асиметричні криптосистемиКонцепція криптосистем з відкритим ключем. Ефективними системами криптографічного захисту даних є асиметричні криптосистеми, які також називають криптосистемами з відкритим ключем. В таких системах для зашифровування даних використовується один ключ, а для розшифровування – інший ключ (звідси і назва – асиметричні). Перший ключ є відкритим і може бути опублікованим для використання усіма користувачами системи, які шифрують дані. Розшифровування даних за допомогою відкритого ключа неможливе. Для розшифровування даних отримувач зашифрованої інформації використовує другий ключ, який є секретним. Зрозуміло, що ключ розшифровування не може бути визначеним з ключа зашифровування. Узагальнена схема асиметричної криптосистеми з відкритим ключем наведена на рис. 5.12. В цій криптосистемі застосовують два різних ключі: КВ – відкритий ключ відправника А; kB – секретний ключ отримувача В. Генератор ключів доцільно розміщувати на стороні отримувача В (щоб не пересилати секретний ключ kB по незахищеному каналу). Значення ключів КВ та kB залежать від початкового стану генератора ключів. Розкриття секретного ключа kB за відомим відкритим ключем КВ повинно бути задачею, яку неможливо розв’язати розрахунковими методами. 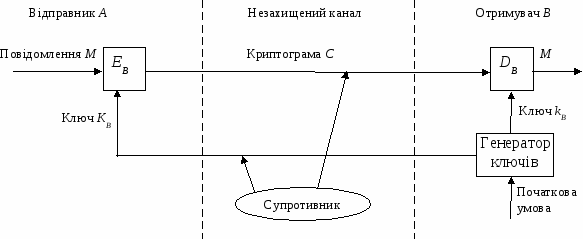 Рис. 5.12. Узагальнена схема асиметричної криптосистеми з відкритим ключем Наведемо характерні особливості асиметричних криптосистем [Error: Reference source not found]:
EB:M→C, DB:C→M є відкритими. Захист інформації в асиметричній криптосистемі базується на секретності ключа kB. У. Діффі та М. Хелман сформулювали вимоги, виконання яких забезпечує безпеку асиметричної криптосистеми [149]:
Однонаправлені функції. Концепція асиметричних криптографічних систем з відкритим ключем базується на застосуванні однонаправлених функцій. Неформально однонаправлену функцію можна визначити наступним чином. Нехай X та Y – довільні множини. Функція f:X→Y є однонаправленою, якщо для всіх xX можна легко обчислити функцію y=f(x), де yY. І в той же час для більшості yY досить складно отримати значення xX, таке, що f(x)=y (при цьому вважають, що існує по крайній мірі одне таке значення х). Основним критерієм віднесення функції f до класу однонаправлених функцій є відсутність ефективних алгоритмів оберенного перетворення Y→X. В якості першого прикладу однонаправленої функції розглянемо цілочисельне множення. Пряма задача – розрахунок добутку двох дуже великих чисел P та Q N=P*Q, є відносно нескладною задачею для ЕОМ. Обернена задача – факторизація великого цілого числа (знаходження дільників P та Q великого цілого числа N=P*Q), є задачею, яку практично неможливо розв’язати засобами сучасних ЕОМ при достатньо великих значеннях N. За сучасними оцінками теорії чисел при цілому N≈2664 та P≈Q для факторизації числа N знадобиться біля 1023 операцій. Іншим характерним прикладом однонаправленої функції є модульна експонента з фіксованими основою та модулем. Нехай A та N – цілі числа, такі, що 1≤A≤N. Визначимо множину ZN: ZN={0,1,2,...,N-1}. Тоді модульна експонента з основою А по модулю N являє собою функцію fA,N:ZN→ZN, fA,N(x)=Ax(mod N), де Х – ціле число, 1≤x≤N-1. Існують ефективні алгоритми, які дозволяють досить швидко розрахувати значення функції fA,N(x). Якщо y=Ax, то природно записати x=logA(y). Тому задачу знаходження функції оберненої до функції fA,N(x) називають задачею знаходження дискретного алгоритму чи задачею дискретного логарифмування. Задача дискретного логарифмування формулюється наступним чином. Для відомих цілих A, N, y знайти ціле число x, таке, що AxmodN=y. Алгоритм розрахунку дискретного логарифму за прийнятний час поки не знайдений. Тому модульна експонента вважається однонаправленою функцією. За сучасними оцінками теорії чисел при цілих числах A2664 та N2664 розв’язання задачі дискретного логарифмування (знаходження показника степеня x для відомого y) потребує біля 1026 операцій – задача має в 1000 раз більшу обчислювальну складність, ніж задача розкладання на множники [Error: Reference source not found]. При збільшенні довжини чисел різниця в оцінках складності задач зростає. Слід зазначити, що поки не вдалося довести, що не існує ефективного алгоритму обчислення дискретного логарифму за прийнятний час. У зв’язку з цим, модульна експонента віднесена до однонаправлених функцій умовно, що, проте, не заважає з успіхом застосовувати її на практиці. Другим важливим класом функцій, що використовуються при побудові криптосистем з відкритим ключем, є так звані однонаправлені функції з „таємним ходом“. Існує неформальне визначення такої функції: функція f:X→Y відноситься до класу одннаправлених функцій з „таємним ходом“ в тому випадку, якщо вона є однонаправленою і, крім того, можливе ефективне обчислення оберненої функції, якщо відомий „таємний хід“ (секретне число, рядок тексту чи інша інформація, що асоціюється з цією функцією). Прикладом такої функції є функція, що використовується в криптосистемі RSA. Криптосистема шифрування даних RSA. Алгоритм RSA було запропоновано в 1978 році трьома авторами: Р. Райвестом (Rivest), А. Шаміром (Shamir) та А. Алдеманом (Aldeman) [150]. Алгоритм названо за першими буквами прізвищ його авторів. Алгоритм RSA став першим повноцінним алгоритмом з відкритим ключем, який може працювати як у режимі шифрування даних, так і в режимі електронного цифрового підпису. Надійність алгоритму базується на складності факторизації великих чисел та складності обчислення дискретних алгоритмів. В криптосистемі RSA відкритий ключ KB, секретний ключ kB, повідомлення М та криптограма С належать множині цілих чисел ZN={0,1,2,...,N-1}, де N – модуль: N=P*Q Тут P і Q – випадкові великі прості числа. Для забезпечення максимальної безпеки P і Q вибирають однакової довжини і зберігають в секреті. Множина ZN з операціями додавання та множення по модулю N утворює арифметику по модулю N. Відкритий ключ KB вибирають відкритим чином так, щоб виконувалися умови: 1<KB(N), НСД(KB,(N))=1, (N)=(P-1)(Q-1) де (N) – функція Ейлера. Функція Ейлера вказує кількість додатніх цілих чисел в інтервалі від 1 до N, які є взаємно простими з N[151]. Друга із вказаних вище умов означає, що відкритий ключ KB та функція Ейлера (N) повинні бути взаємно простими (їх найбільший спільний дільник (НСД) повинен бути рівним 1). Далі, використовуючи розширений алгоритм Евкліда, розраховують секретний ключ kB, який задовольняє наступній умові: kB*KB1(mod(N)), або kB=KB-1(mod(P-1)(Q-1)). Цей ключ легко розрахувати, оскільки отримувач знає пару простих чисел (P,Q) і може легко розрахувати (N). Нагадаємо, що kB та N повинні бути взаємно простими. Відкритий ключ KB використовують для шифрування даних, а секретний ключ kB – для розшифровування. Перетворення шифрування визначає криптограму С через пару (відкритий ключ KB, повідомлення М) відповідно до формули: Знаходження функції, оберненої до Проте обернену задачу – розшифровування криптограми С, – можна розв’язати, використовуючи пару – секретний ключ kB та криптограма С за формулою: Таким чином, якщо криптограму піднести до степеня kB, то в результаті відновлюється вихідний відкритий текст М, оскільки Таким чином, отримувач, який створює криптосистему, захищає два параметри: 1) секретний ключ kB та 2) пару чисел (P,Q), добуток яких дає значення N. З іншої сторони, отримувач відкриває значення модуля N та відкритий ключ KB. Противнику відомі тільки значення KB та N. Якщо б він зміг розкласти число N на множники P та Q, він зміг би обчислити значення функції Ейлера (N)=(P-1)(Q-1) та визначити значення секретного ключа kB. Проте, як уже зазначалося, факторизація дуже великого N за допомогою обчислень є нездійсненною на даний час задачею (за умови, що довжина вибраних P та Q складає достатню кількість десяткових знаків). Безпека та швидкодія криптосистеми RSA. Безпека алгоритму RSA базується на складності розв’язання задач факторизації великих чисел, які є добутком двох великих простих чисел. Дійсно, криптостійкість алгоритму RSA визначається тим, що після формування секретного ключа kB та відкритого ключа KB знищуються значення простих чисел P та Q, і тоді виключно складно визначити секретний ключ kB за відкритим ключем KB, оскільки для цього потрібно розв’язати задачу знаходження дільників P і Q та модуля N. Розкладання величини N на прості множники P та Q дозволяє обчислити функцію (N)=(P-1)(Q-1) та визначити секретне значення kB, використовуючи рівняння: KB*kB1(mod(N)). Іншим можливим способом криптоаналізу алгоритму RSA є безпосереднє обчислення чи підбір значення функції (N)=(P-1)(Q-1). Якщо визначено значення (N), то співмножники P та Q обчислюються досить просто, проте така задача не простіша за факторизацію модуля N. Задача факторизації є складною задачею для великих значень модуля N. Спочатку автори алгоритму RSA пропонували для обчислення модуля N вибирати прості числа P та Q випадковим чином по 50 десяткових розрядів кожне. Вважалося, що такі великі числа N досить складно розкласти на прості множники. Один із авторів алгоритму RSA, Р.Райвест вважав, що для розкладання на прості множники числа із майже 130 десяткових цифр, наведеного у їх публікації, знадобиться більше 40 квадрільйонів років машинного часу [Error: Reference source not found]. Проте цей прогноз не виправдався у зв’язку з відносно швидким прогресом комп’ютерів та їх обчислювальної потужності, а також покращення алгоритмів факторизації. Один із найшвидших алгоритмів факторизації, відомих в наш час, – алгоритм NFS (Number Field Sieve) може виконати факторизацію великого числа N (з кількістю десяткових розрядів більше 120) за кількість кроків, яка оцінюється величиною [152] В 1994 році було факторизовано число із 129 десятковими знаками [153]. Це вдалося здійснити математикам А.Ленстра та М.Манассі з використанням організації розподілених обчислень на 1600 комп’ютерах, об’єднаних в мережу, на протязі восьми місяців. На думку А.Ленстра та М.Манассі, їх робота компрометує криптосистеми RSA та створює велику загрозу їх подальшим застосуванням. Тепер розробники криптоалгоритмів з відкритим ключем на базі RSA змушені уникати використання чисел довжиною менше 200 десяткових розрядів (таке число було факторизовано в 2005 році [Error: Reference source not found]). Останні публікації пропонують застосовувати для цього числа довжиною не менше 250-300 десяткових розрядів. Криптографи спробували розрахувати безпечні довжини ключів асиметричних криптосистем на найближчі 20 років виходячи з прогнозу розвитку комп’ютерів та їх обчислювальної потужності а також можливого удосконалення алгоритмів факторизації. Ці оцінки представлені в табл. 5.4. Оціночні дані наведено для трьох груп користувачів, відповідно до рівня вимог до їх інформаційної безпеки. Таблиця 5.4. Оцінки довжини ключів для асиметричних криптосистем, біт
Криптосистеми RSA реалізуються як апаратними, так і програмними засобами. Для апаратної реалізації операцій зашифровування та розшифровування RSA розроблено спеціальні процесори, які дозволяють виконувати операції, пов’язані з піднесенням до степеня по модулю N за відносно короткий час. І всеж таки апаратна реалізація RSA є приблизно в 100 разів повільнішою апаратної реалізації симетричного криптоалгоритму DES. Програмна реалізація RSA також приблизно в 100 разів повільніша програмної реалізації DES. З розвитком технологій ці оцінки можуть дещо змінюватися, але асиметрична криптосистема RSA ніколи не досягне швидкодії симетричних криптосистем. Слід зазначити, що невелика швидкодія криптосистем RSA обмежує область їх застосування, але не перекреслює їх цінності. Схема шифрування Поліга-Хеллмана. Схема шифрування Поліга-Хеллмана подібна до схеми шифрування RSA. Вона представляє собою несиметричний алгоритм, оскільки використовуються різні ключі для шифрування і розшифровування. В той же час цю схему не можна віднести до класу криптосистем з відкритим ключем, оскільки ключі шифрування та розшифровування легко виводяться один з одного [154]. Обидва ключі потрібно тримати у секреті. Аналогічно до системи RSA криптограма С та відкритий текст P визначається із співвідношень: C=Pemodn, P=Cdmodn. де e*d1 (по модулю деякого числа n). На відміну від алгоритму RSA в цій схемі число n не визначається через два великі прості числа; число n повинно залишатися частиною секретного ключа. Якщо хтось знатиме e та n, то він зможе розрахувати значання d. Не знаючи значень e чи d, противник буде змушений розраховувати значення e=logPC(modn). Відомо, що це є складною задачею. Схема шифрування Поліга-Хеллмана запатентована в США та Канаді. Схема шифрування Ель Гамаля. Схема Ель Гамаля, запропонована в 1985 році, може використовуватися як для шифрування, так і для цифрових підписів. Безпека схеми Ель Гамаля зумовлена складністю розрахунку дискретних логарифмів в кінцевому полі [155]. Для генерації пари ключів (відкритий ключ – секретний ключ), спочатку вибирають деяке велике просте число P та велике ціле число G, причому G<P. Числа P та G можуть бути розповсюджені серед групи користувачів. Потім вибирають випадкове число Х, причому Х<P. Число X є секретним ключем і повинно зберігатися в таємниці. Потім обчислюють Y=GXmodP. Число Y є відкритим ключем. Для того, щоб зашифрувати повідомлення M, вибирають випадкове ціле число K, 1<K<P-1, таке, що числа K та (P-1) є взаємно простими. Потім вираховують числа a=GKmodP, b=YKMmodP. Пара чисел (a,b) є шифротекстом. Зазначимо, що довжина шифротексту вдвічі більша довжини вихідного відкритого тексту M. Для розшифровування шифротексту (a,b), обчислюють M=b/aXmodP. Комбінований метод шифрування. Головною перевагою криптосистем з відкритим ключем є їх потенційно висока безпека: немає необхідності ні передавати, ні повідомляти будь-кому значення секретних ключів, ні впевнюватися в їх справжності. Проте алгоритми, що лежать в основі криптосистем з відкритим ключем, мають ряд недоліків:
У зв’язку з цим швидкодія криптосистем з відкритим ключем зазвичай в сотні та більше разів нижча швидкодії симетричних криптосистем. Комбінований (гібридний) метод шифрування дозволяє поєднувати переваги високої секретності, притаманні асиметричним системам з відкритим ключем, з перевагами високої швидкості роботи, які притаманні криптосистемам із секретним ключем. При такому підході криптосистема з відкритим ключем застосовується тільки для шифрування, передачі та наступного розшифровування тільки секретного ключа симетричної криптосистеми. А симетрична криптосистема застосовується для шифрування і передачі вихідного відкритого тексту. В результаті криптосистема з відкритим ключем не заміняє симетричну криптосистему з секретним ключем, а тільки доповнює її, забезпечуючи кращу захищеність інформації. Такий підхід іноді називають схемою електронного цифрового конверта. Якщо користувач А хоче передати зашифроване комбінованим методом повідомлення М користувачу В, то порядок його дій буде наступним.
Дії користувача B при отриманні зашифрованого повідомлення та зашифрованого сеансового ключа повинні бути зворотніми:
При використанні комбінованого методу шифрування можна бути впевненим в тому, що тільки користувач В зможе правильно розшифрувати ключ KS та прочитати повідомлення М. Таким чином, при комбінованому методі шифрування застосовуються криптографічні ключі як симетричних, так і асиметричних криптосистем. Очевидно, що вибір довжин ключів для кожного типу криптосистеми слід здійснювати таким чином, щоб зловмиснику було однаково складно атакувати будь-який механізм захисту комбінованої криптосистеми. В табл. 5.5 наведено розповсюджені довжини ключів симетричних та асиметричних криптосистем, для яких складність атаки повного перебору приблизно рівна складності факторизації відповідних модулів асиметричних криптосистем. Таблиця 5.5 Довжини ключів для симетричних та асиметричних криптосистем при однаковій їх криптостійкості
Комбінований метод допускає можливість виконання процедури автентифікації. Для цього користувач А на основі функції хешування повідомлення та свого секретного ключа kA за допомогою відомого алгоритму електронного цифрового підпису генерує свій підпис та записує його, наприклад, в кінець повідомлення. Користувач В, прочитавши прийняте повідомлення, може впевнитися в справжності цифрового підпису абонента А. Використовуючи той же алгоритм електронного цифрового підпису та результат хешування прийнятого повідомлення, користувач В перевіряє отриманий підпис. Комбінований метод шифрування є найбільш раціональним, оскільки поєднує в собі високу швидкодію симетричного шифрування та високу криптостійкість, яку гарантують системи з відкритим ключем. |
