|
|
Барасюк Я. М
5.2.5. Електронний цифровий підпис
Проблема автентифікації даних та електронний цифровий підпис. При обміні електронними документами по мережі суттєво знижуються затрати на обробку та зберігання документів. Однак при цьому виникає проблема автентифікації автора документу та самого документу – встановлення автентичності автора та відсутності змін в отриманому документі. При звичайному (паперовому) документообгові ці проблеми вирішуються за рахунок того, що інформація в документі та рукописний підпис автора жорстко зв’язані з фізичним носієм (папером). В електронних документах на машинних носіях такого зв’язку немає.
Метою автентифікації електронних документів є їх захист від можливих видів зловмисних дій, до яких відносяться [Error: Reference source not found]:
активне перехоплення – порушник, підключившись до мережі, перехоплює документи (файли) і змінює їх;
маскарад – абонент С посилає документ абоненту В від імені абонента А;
ренегатство– абонент А заявляє, що не відправляв повідомлення абоненту В, хоча в дійсності відправляв;
підміна– абонент В змінює чи формує новий документ і заявляє, що отримав його від абонента А;
повтор– абонент С повторює переданий раніше документ, який абонент А відправляв абоненту В.
Ці види зловмисних дій можуть нанести суттєві збитки різноманітним підприємствам, організаціям та приватним особам, що застосовують у своїй діяльності комп’ютерні інформаційні технології. При обробці документів в електронній формі стають непридатними традиційні способи встановлення автентичності за рукописним підписом та відтиском печатки на паперовому документі. Принципово новим рішенням є електронний цифровий підпис (ЕЦП).
Електронний цифровий підпис використовується для автентифікації файлів, що передаються по телекомунікаційних каналах зв’язку. Функціонально він аналогічний звичайному рукописному підпису і володіє усіма його основними перевагами:
засвідчує, що підписаний документ виходить від особи, яка поставила свій підпис;
не дає цій особі можливості відмовитися від обов’язків, зв’язаних із підписаним документом;
гарантує цілісність підписаного документу.
Цифровий підпис представляє собою відносно невеликий об’єм додаткової цифрової інформації, що передається разом із підписаним документом.
Система ЕЦП включає дві процедури: 1) процедуру встановлення підпису; 2) процедуру перевірки підпису. У процедурі встановлення підпису використовується секретний ключ відправника повідомлення, в процедурі перевірки підпису – відкритий ключ відправника.
При формуванні ЕЦП відправник у першу чергу обчислює хеш-функцію h(M) підписуваного тексту М. Обчислене значення хеш-функції h(M) представляє собою один короткий блок інформації m, який характеризує весь текст М в цілому. Потім число m шифрується секретним ключем відправника. Отримана при цьому пара чисел представляє собою ЕЦП для даного тексту М. При перевірці ЕЦП отримувач повідомлення знову обчислює хеш-функцію m=h(M) прийнятого по каналу зв’язку тексту М, після чого за допомогою відкритого ключа відправника перевіряє, чи відповідає отриманий підпис обчисленому значенню m хеш-функції.
Принциповим моментом в системі ЕЦП є неможливість підробки ЕЦП користувача без знання його секретного ключа підписування. В якості підписуваного документу може бути використано будь-який файл. Підписаний файл створюється із непідписаного шляхом додавання до нього одного чи більше електронних підписів. Кожний підпис вміщує наступну інформацію [Error: Reference source not found]:
дату підпису;
термін закінчення дії ключа даного підпису;
інформацію про особу, що підписала файл (ПІП, посада, скорочена назва підприємства/організації);
ідентифікатор особи, яка підписала документ (ім’я відкритого ключа);
власне, сам цифровий підпис.
Однонаправлені хеш-функції. Хеш-функція призначена для стиснення підписуваного документу М до кількох десятків чи сотень біт. Хеш-функція h() приймає в якості аргументу повідомлення (документ) М довільної довжини і повертає хеш-значення h(M)=H фіксованої довжини. Зазвичай хешована інформація є стиснутим двійковим представленням основного повідомлення довільної довжини. Слід зазначити, що значення хеш-функції h(M) складним чином залежить від документу М і не дозволяє відновити сам документ М. Хеш-функція повинна задовольняти цілому ряду умов [158]:
хеш-функція повинна бути чутливою до усіх можливих змін в тексті М, таким як вставки, видалення, перестановки тощо;
хеш-функція повинна мати властивості необоротності – задача підбору документу М', який би володів потрібним значенням хеш-функції повинна бути нерозв’язною обчислювальними методами;
ймовірність того, що значення хеш-функцій двох різних документів (не залежно від їх довжини) співпадуть, повинна бути надзвичайно малою.
Більшість хеш-функцій будується на основі однонаправленої функції f(), яка утворює вихідне значення довжиною n при заданні двох вхідних значень довжиною n. Цими вхідними значеннями є блок вихідного тексту Мі та хеш-значення Hi-1 попереднього блоку тексту, рис. 5.15:
Hi=f(Mi,Hi-1).
Хеш-значення, яке обчислюється для останнього блоку тексту стає хеш-значенням всього повідомлення М. В результаті однонаправлена хеш-функція завжди формує вихід фіксованої довжини n, незалежно від довжини вхідного тексту.

Рис. 5.15. Побудова однонаправленої функції
Однонаправлені хеш-функції на основі симетричних блочних алгоритмів. Однонаправлену хеш-функцію можна побудувати, використовуючи симетричний блочний алгоритм. Найбільш очевидний підхід полягає в тому, щоб шифрувати повідомлення М з використанням блочного алгоритму в режимі CBC чи CFB за допомогою фіксованого ключа та деякого вектора ініціалізації IV. Останній блок шифротексту можна розглядати в якості хеш-значення повідомлення М. При такому підході не завжди можна побудувати безпечну однонаправлену хеш-функцію, але завжди можна отримати код автентифікації повідомлення MAC (Message Autentication Code).
Безпечніший варіант хеш-функції можна отримати, використовуючи блок повідомлення в якості ключа, попереднє хеш-значення – в якості входу, а поточне хеш-значення – в якості виходу. Реальні хеш-функції проектуються іще складніше. Довжина блоку зазвичай визначається довжиною ключа, а довжина хеш-значення співпадає з довжиною блоку. Оскільки більшість блочних алгоритмів є 64-бітними, деякі схеми хешування проектують так, щоб хеш-значення мало довжину, рівну подвійній довжині блоку.
Якщо прийняти, що отримується коректна хеш-функція, безпека системи хешування базується на безпеці блочного алгоритму, що лежить в її основі. Схема хешування, у якої довжина хеш-значення рівна довжині блоку, наведена на рис. 5.16.
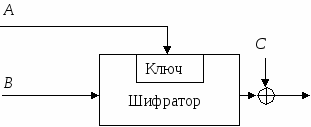
Рис. 5.16. Узагальнена схема формування хеш-функції
Робота цієї схеми описується виразами:
Ho=IH,
Hi=EA(B)C,
де IH – деяке випадкове початкове значення; А, В та С можуть приймати значення Mi, Hi-1, (MiHi-1) або бути константами. Повідомлення М розбивається на блоки Мі прийнятої довжини, які обробляються один за одним.
Три різні змінні А, В та С можуть приймати одне із чотирьох можливих значень, у зв’язку з чим в принципі можна отримати 64 варіанти загальної схеми цього типу. Із них 52 варіанти є або тривіально слабкими, або небезпечними. Інші 12 безпечних схем хешування наведено в табл. 5.8.
Таблиця 5.8
Схеми безпечного хешування
у яких довжина хеш-значення рівна довжині блоку
Номер схеми
|
Функція хешування
|
1
|
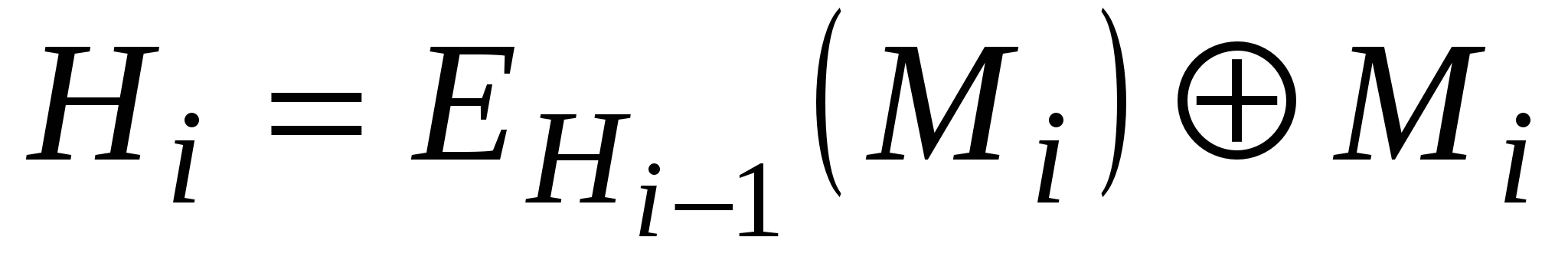
|
2
|

|
3
|
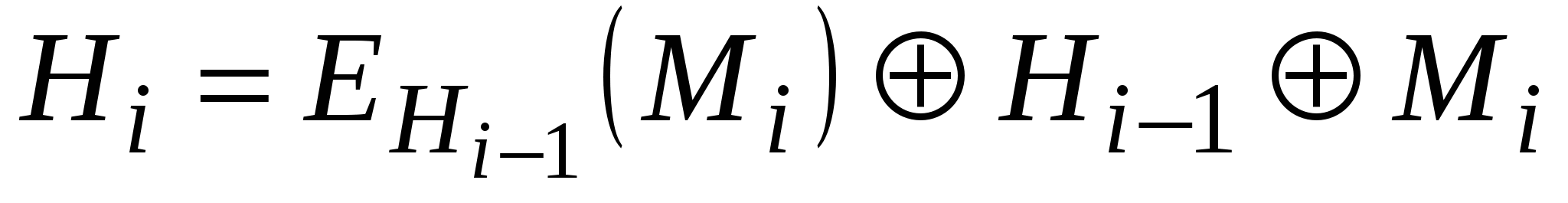
|
4
|
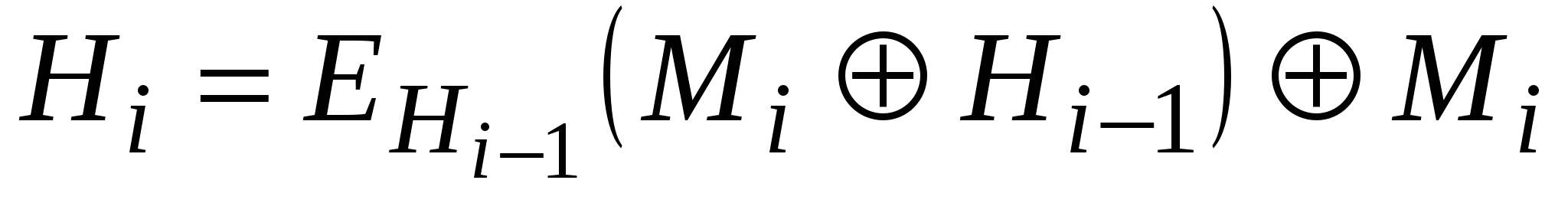
|
5
|
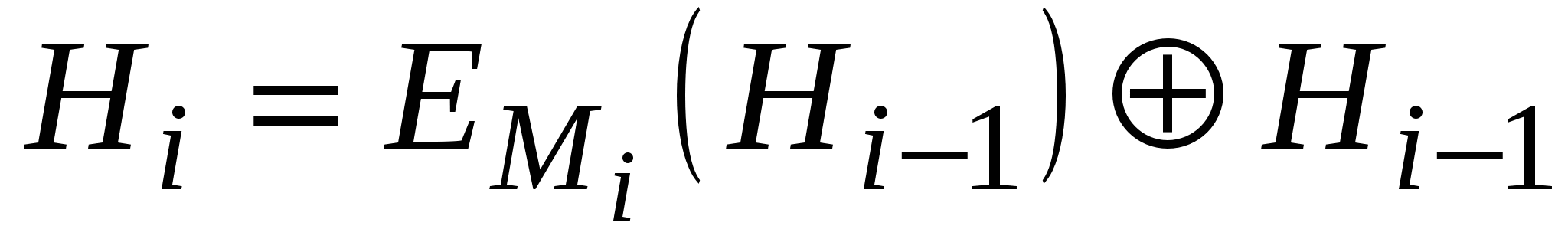
|
6
|

|
7
|
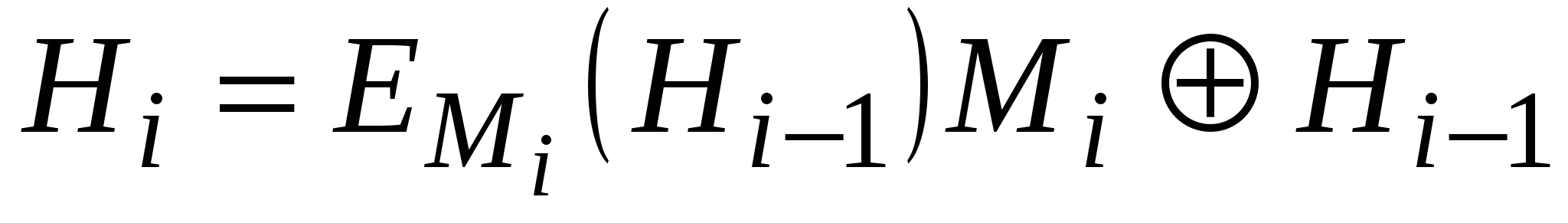
|
8
|
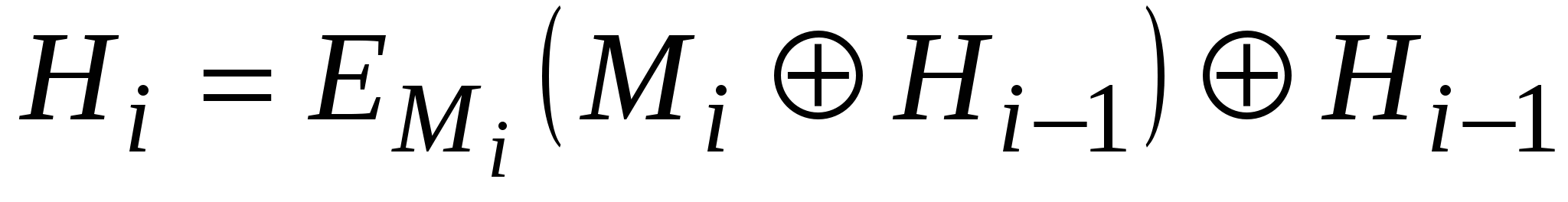
|
9
|
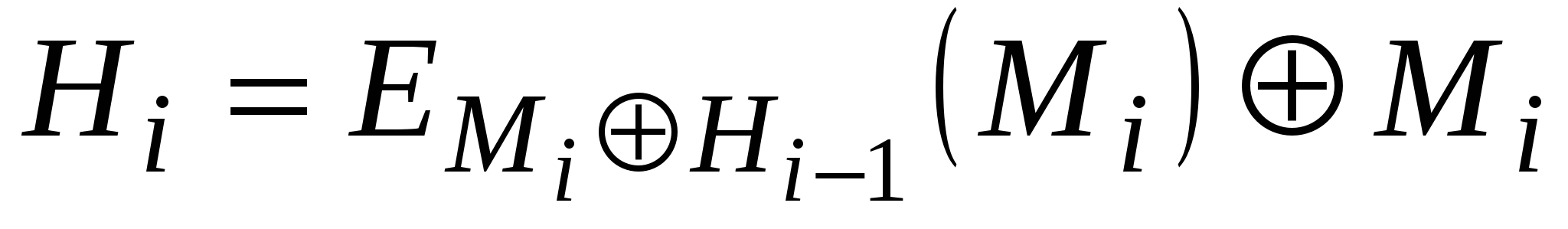
|
10
|
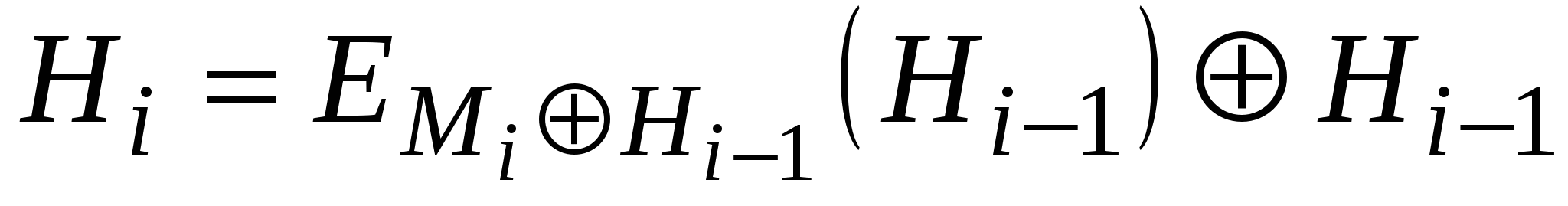
|
11
|
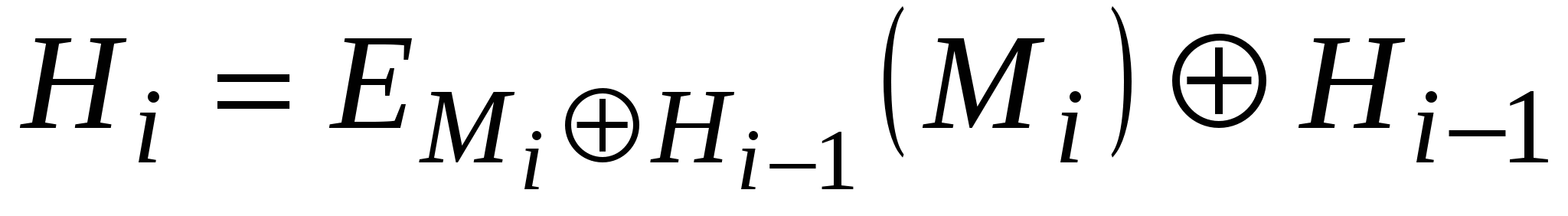
|
12
|
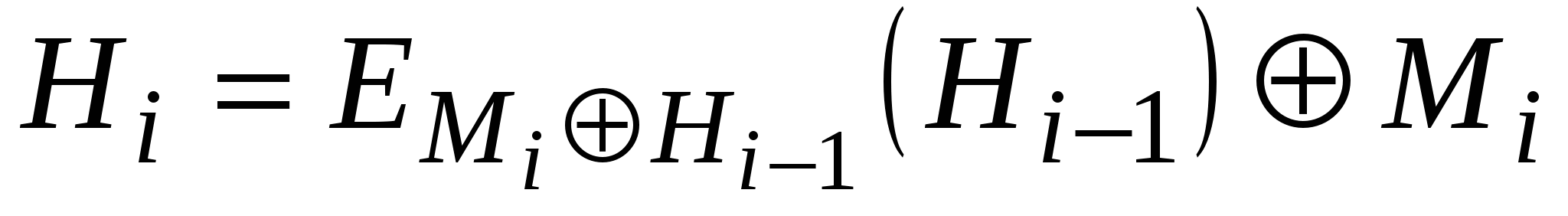
|
Перші чотири з цих схем, які є безпечними при усіх атаках, графічно представлені на рис. 5.17.
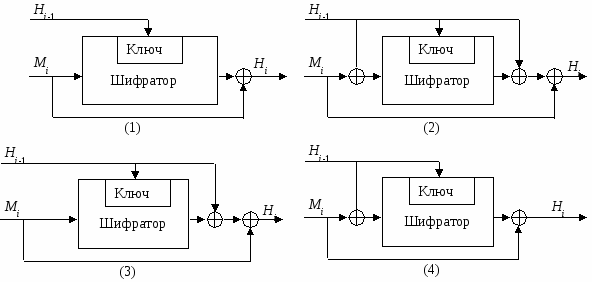
Рис. 5.17. Чотири схеми безпечного хешування
Алгоритми електронного цифрового підпису. Технологія застосування системи ЕЦП передбачає наявність мережі абонентів, які пересилають один одному підписані електронні документи. Для кожного абонента генерується пара ключів: секретний та відкритий. Секретний ключ зберігається абонентом у таємниці і використовується ним для формування ЕЦП. Відкритий ключ відомий усім іншим користувачам і призначений для перевірки ЕЦП отримувачем підписаного електронного документу. Відкритий ключ не дозволяє вирахувати секретний ключ.
Для генерації пари ключів (секретного та відкритого) в алгоритмах ЕЦП, як і в асиметричних системах шифрування, використовують різні математичні схеми, що базуються на використанні однонаправлених функції. Ці схеми поділяються на дві групи. В основі такого поділу лежать відомі складні обчислювальні задачі:
задача факторизації (розкладання на множники) великих цілих чисел;
задача дискретного логарифмування.
Алгоритм цифрового підпису RSA. Першою реально працюючою і найвідомішою в усьому світі системою ЕЦП стала система RSA, математична схема якої була розроблена у 1977 році в Масачусетському технологічному інституті США [159].
Спочатку потрібно обчислити пару ключів (секретний та відкритий). Для цього відправник (автор) електронних документів обчислює два великих простих числа P та Q, після чого знаходить їх добуток
N=PQ
і значення функції
(N)=(P-1)(Q-1).
Далі відправник обчислює число Е з умов:
E≤(N), НСД(E, (N))=1
та число D з умов:
D<N, ED1(mod (N)).
Пара чисел (E,N) є відкритим ключем. Цю пару чисел автор передає партнерам по переписці для перевірки його цифрових підписів. Число D зберігається автором як секретний ключ для підписування. Узагальнена схема формування та перевірки цифрового підпису RSA представлена на рис. 5.18. Припустимо, що відправник хоче підписати повідомлення М перед його відправкою. Спочатку повідомлення М стискують за допомогою хеш-функції h() в ціле число m:
m=h(M).
Потім розраховують цифровий підпис S під електронним документом М, використовуючи хеш-значення m та секретний ключ D:
S=mD(mod N).
Пара (M,S) передається партнеру-отримувачу як електронний документ М, підписаний цифровим підписом S, причому підпис S сформовано власником секретного ключа D.
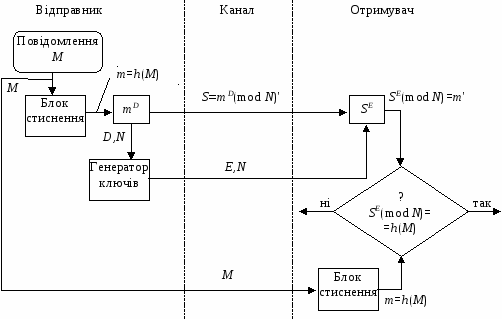
Рис. 5.18. Узагальнена схема цифрового підпису RSA
Після прийому пари (M,S) отримувач обчислює хеш-значення повідомлення М двома різними способами. Перш за все він відновлює хеш-значення m', застосовуючи криптографічне перетворення підпису S з використанням відкритого ключа Е:
m'=SE(mod N).
Крім того, він знаходить результат хешування прийнятого повідомлення М за допомогою такої ж хеш-функції h():
m=h(M).
Якщо підтверджується рівність обчислених значень:
SE(mod N)=h(M),
то отримувач визнає пару (M,S) автентичною. Доведено, що тільки власник секретного ключа D може генерувати цифровий підпис S для документу М, а визначити секретне число D по відкритому ключу Е не легше, ніж розкласти модуль N на множники.
Крім того, можна строго математично довести, що результат перевірки цифрового підпису S буде позитивним тільки в тому випадку, якщо при обчисленні S було використано секретний ключ D, який відповідає відкритому ключу Е. Тому відкритий ключ Е іноді називають „ідентифікатором“ підписуючого.
На жаль, алгоритм електронного цифрового підпису RSA має ряд недоліків [160]:
При обчисленні модуля N, ключів Е та D для системи цифрового підпису RSA необхідно перевірити більшу кількість додаткових умов, що досить складно реалізувати практично. Невиконання будь-якої з цих умов робить можливим фальсифікацію цифрового підпису зі сторони того, хто виявить таке невиконання. При підписуванні важливих документів не можна допускати таку можливість навіть теоретично.
Для забезпечення криптостійкості цифрового підпису RSA по відношенню до спроб фальсифікації на рівні, наприклад, національного стандарту США на шифрування інформації (1018), необхідно використовувати при обчисленнях N, D та E цілі числа не менше 2512 (біля 10154) кожне, що вимагає великих обчислювальних затрат, що перевищують на 20-30% обчислювальні затрати інших алгоритмів цифрового підпису при збереженні того ж рівня криптостійкості.
Цифровий підпис RSA вразливий до так званої мультиплікативної атаки. Інакше кажучи, алгоритм цифрового підпису RSA дозволяє зловмиснику без знання секретного ключа D сформувати підписи під тими документами, у яких результат хешування можна обчислити як добуток результатів хешування уже підписаних документів.
Алгоритм цифрового підпису Ель Гамаля (EGSA). Більш надійний та зручний для реалізації на персональних комп’ютерах алгоритм цифрового підпису був розроблений в 1984 році американцем арабського походження Тахером Ель Гамалем. В 1991 році цей алгоритм був прийнятий за основу для національного стандарту США [Error: Reference source not found].
Назва EGSA походить від слів El Gamal Signature Algorithm (алгоритм цифрового підпису Ель Гамаля). Ідея EGSA базується на тому, що для обгрунтування практичної неможливості фальсифікації цифрового підпису може бути використана більш складна обчислювальна задача ніж розкладання на множники великого цілого числа, – задача дискретного логарифмування. Крім того, Ель Гамалю вдалося уникнути явної слабкості алгоритму цифрового підпису RSA, пов’язаної з можливістю підробки цифрового підпису під деякими повідомленнями без визначення секретного ключа.
Розглянемо детальніше алгоритм цифрового підпису Ель Гамаля. Для генерації пари ключів (відкритий ключ – секретний ключ), спочатку вибирають деяке велике просте число Р та велике просте число G, причому G<P. Відправник та отримувач підписаного документу використовують при обчисленнях однакові великі цілі числа Р (
10308 або
21024) та G (
10154 або
2512), які не є секретними. Відправник вибирає випадкове ціле число Х, 1<X≤(P-1), та обчислює
Y=GX modP.
Число Y є відкритим ключем, який використовується для перевірки підпису відправника. Число Y відкрито передається усім потенційним отримувачам документів. Число X є секретним ключем відправника для підписування документів та повинно зберігатися в секреті.
Для того, щоб підписати повідомлення M, відправник спочатку його хешує за допомогою хеш-функції h() в ціле число m:
m=h(M), 1<m<(P-1),
та генерує випадкове ціле число К, 1<К<(P-1), таке, що К та (P-1) є взаємно простими. Потім відправник обчислює ціле число a:
a=GK modP
і, застосовуючи розширений алгоритм Евкліда, обчислює за допомогою секретного ключа Х ціле число b з рівняння
m=X*a+K*b(mod(P-1).
пара чисел (a,b) утворює цифровий підпис S:
S=(a,b),
який проставляється під документом М.
Трійка чисел (M,a,b) передається отримувачу, тоді як пара чисел (X,K) тримається у секреті. Після прийому підписаного повідомлення (M,a,b) отримувач повинен перевірити, чи відповідає підпис S=(a,b) повідомленню M. Для цього отримувач спочатку обчислює за прийнятим повідомленням М число
m=h(M),
(хешує прийняте повідомлення М). Потім отримувач обчислює значення
A=YaAb(modP)
та визнає повідомлення М автентичним, якщо, і тільки якщо
A=Gm(modP).
Іншими словами, отримувач перевіряє справедливість співвідношення
YaAb(modP)=Gm(modP).
Можна строго математично довести, що остання рівність буде виконуватися тоді, і тільки тоді, коли підпис S=(a,b) під документом М отриманий за допомогою саме того секретного ключа Х, з якого було отримано відкритий ключ Y. Таким чином, можна надійно впевнитися, що відправником повідомлення М був власник саме даного секретного ключа X, не розкриваючи при цьому сам ключ, і те, що відправник підписав саме цей конкретний документ М.
Слід відмітити, що виконання кожного підпису за методом Ель Гамаля вимагає нового значення К, причому це значення повинно вибиратися випадковим чином. Якщо зловмисник колись розкриє значення К, яке повторно використовується відправником, то він зможе розкрити секретний ключ Х відправника. Також слід відмітити, що схема Ель Гамаля є характерним прикладом підходу, який допускає пересилку повідомлення М у відкритій формі разом з приєднаним автентифікатором (a,b). В таких випадках процедура встановлення автентичності прийнятого повідомлення полягає в перевірці відповідності автентифікатора повідомленню.
Схема цифрового підпису Ель Гамаля має ряд переваг порівняно зі схемою цифрового підпису RSA [Error: Reference source not found]:
При заданому рівні стійкості алгоритму цифрового підпису цілі числа, що приймають участь в обчисленнях, мають на 25% коротший запис, що зменшує складність обчислень майже у два рази і дозволяє значно скоротити об’єм використовваної пам’яті.
При виборі модуля Р досить перевірити, що це число є простим і що у числа (Р-1) є великий простий множник (всього дві умови, які легко перевіряються).
Процедура формування підпису за схемою Ель Гамаля не дозволяє обчислити цифрові підписи під новими повідомленнями без знання секретного ключа (як у RSA).
Проте алгоритм цифрового підпису Ель Гамаля має і деякі недоліки порівняно зі схемою підпису RSA. Зокрема, довжина цифрового підпису отримується в 1,5 рази більшою, що, у свою чергу, збільшує час її обчислення.
Алгоритм цифрового підпису DSA. Алгоритм цифрового підпису DSA (Digital Signature Algorithm) запропонований в 1991 році у США для використання у стандарті цифрового підпису DSS (Digital Signature Standard) [161]. Алгоритм DSA є розвитком алгоритмів цифрового підпису Ель Гамаля та К. Шнорра.
Відправник та отримувач електронного документу використовують при обчисленні великі цілі числа: G та P – прості числа, L біт кожне (512≤L≤1024); q – просте число, довжиною 160 біт (дільник числа (Р-1)). Числа G, P, q є відкритими і можуть бути спільними для всіх користувачів мережі. Відправник вибирає випадкове ціле число Х, 1<X<q. Число X є секретним ключем відправника для формування електронного цифрового підпису. Потім відправник обчислює значення
Y=GX modP.
Число Y є відкритим ключем для перевірки підпису відправника. Число Y передається усім отримувачам документів.
Цей алгоритм також передбачає використання односторонньої функції хешування h(). У стандарті DSS визначено алгоритм безпечного хешування SHA (Secure Hash Algorithm). Для того, щоб підписати документ М, відправник хешує його в ціле хеш-значення m:
m=h(M), 1<m<q,
потім генерує випадкове ціле число K, 1<K<q, та обчислює число r:
r=(GK modP) modq.
Потім відправник обчислює за допомогою секретного ключа Х ціле число s:
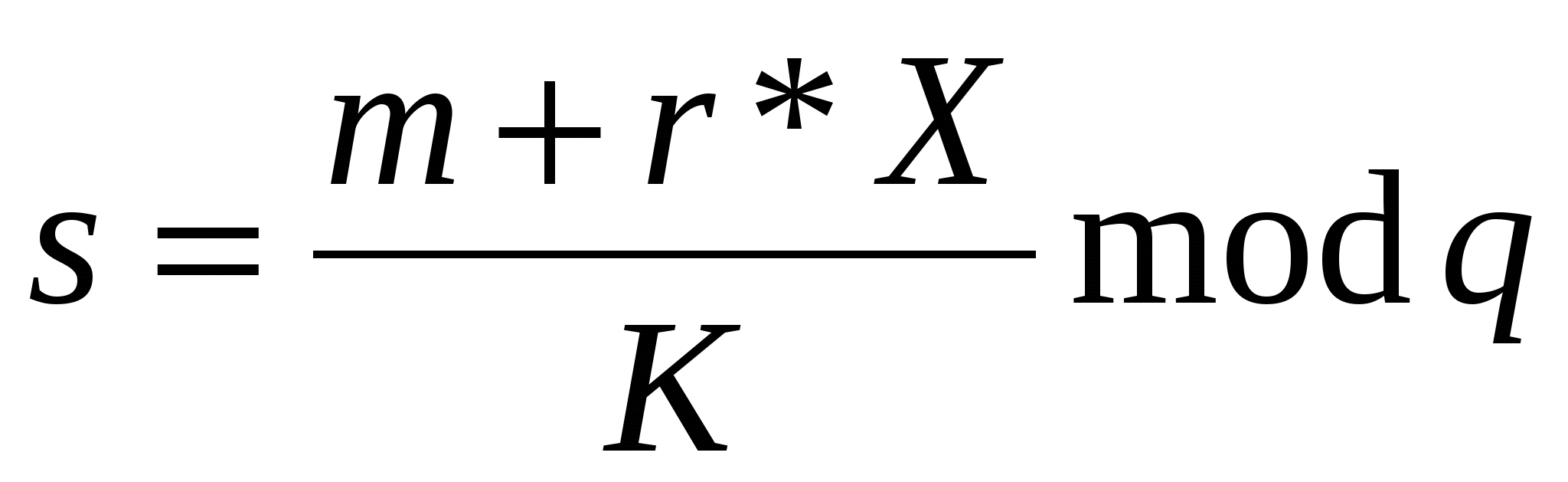 . .
Пара чисел r та s утворює цифровий підпис
S=(r,s)
під документом М. Таким чином, підписане повідомлення представляє собою трійку чисел (M,r,s).
Отримувач підписаного повідомлення (M,r,s) перевіряє виконання умов
0<r<q, 0<s<q
і відхиляє підпис, якщо хоча б одна із цих умов не виконана. Якщо обидві умови виконуються, отримувач обчислює значення
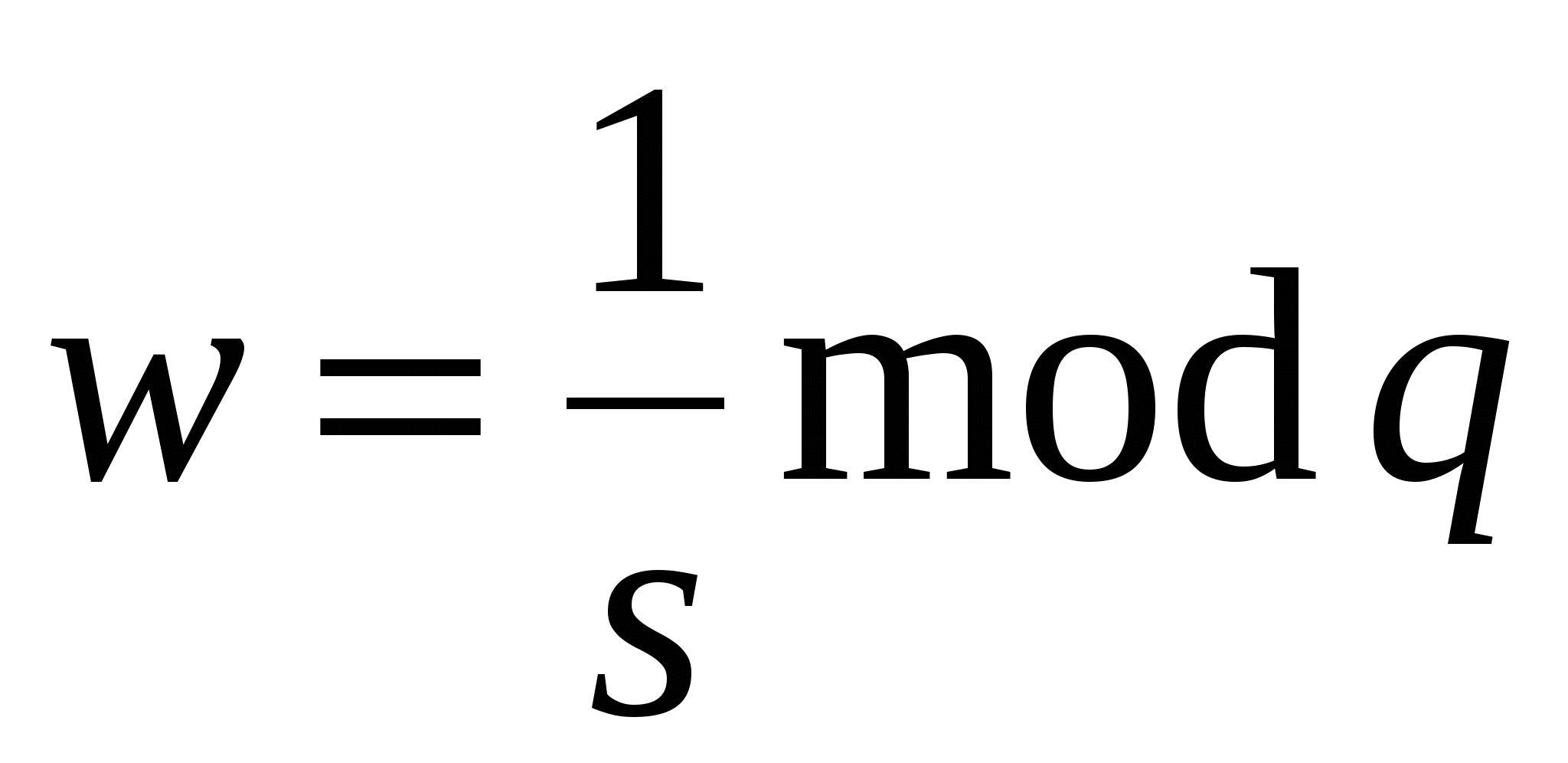 , ,
хеш-значення
m=h(M)
та числа
u1=(m*w) modq,
u2=(r*w) modq.
Далі отримувач за допомогою відкритого ключа Y обчислює значення
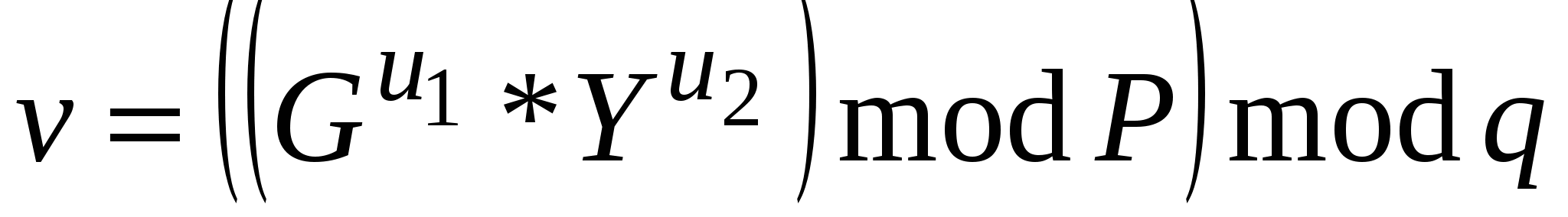
та перевіряє виконання умови v=r. Якщо ця умова виконується, тоді підпис S=(r,s) під документом М визнається отримувачем справжньою.
Можна строго математично довести, що остання рівність буде виконуватися тоді, і тільки тоді, коли підпис S=(r,s) під документом М отримано за допомогою саме того секретного ключа Х, з якого було отримано відкритий ключ Y. Таким чином можна надійно впевнитись, що відправник повідомлення володіє саме даним секретним ключем Х (не розкриваючи при цьому значення ключа Х) і що відправник підписав саме даний документ М.
Порівняно з алгоритмом цифрового підпису Ель Гамаля алгоритм DSA має ряд переваг [Error: Reference source not found]:
При довільному допустимому рівні стійкості (при будь-якій парі чисел G і Р (від 512 до 1024 біт)), числа q, X, r, s мають довжину по 160 біт, скорочуючи довжину підпису до 320 біт.
Більшість операцій з числами K, r, s, X при обчисленні підпису здійснюється по модулю числа q, довжиною 160 біт, що скорочує час обчислення підпису.
При перевірці підпису більшість операцій з числами u1, u2, v, w також здійснюється за модулем числа q, довжиною 160 біт, що скорочує об’єм пам’яті та час обчислення.
Недоліком алгоритму DSA є те, що при підписуванні та при перевірці підпису потрібно виконувати складні операції ділення по модулю q:
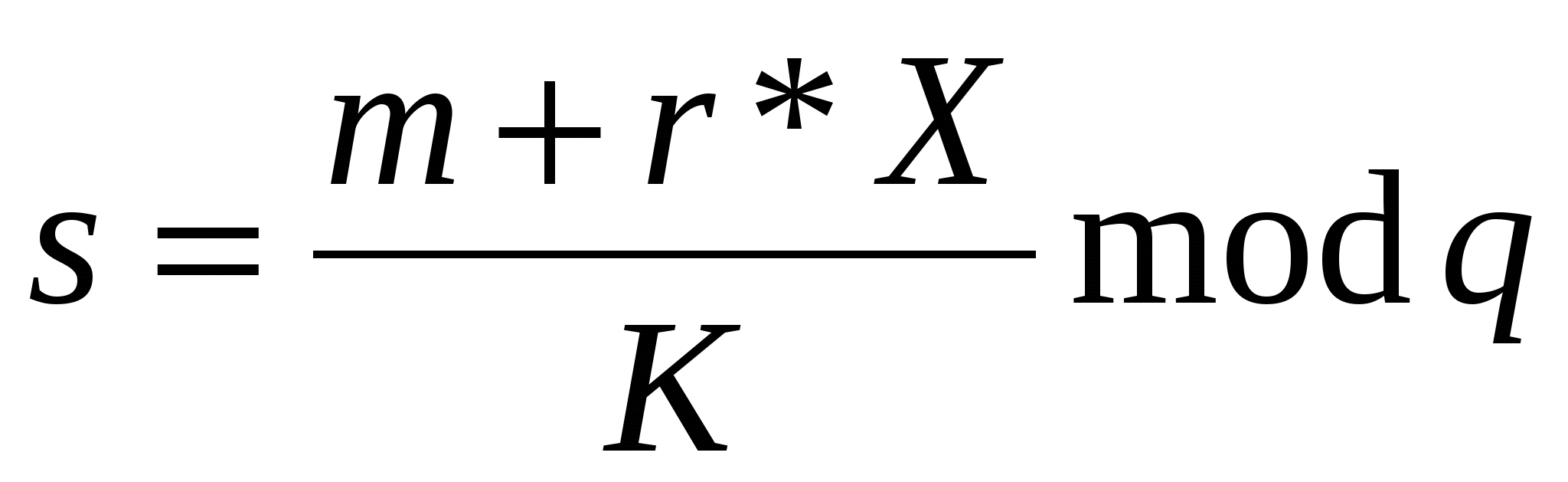 , , 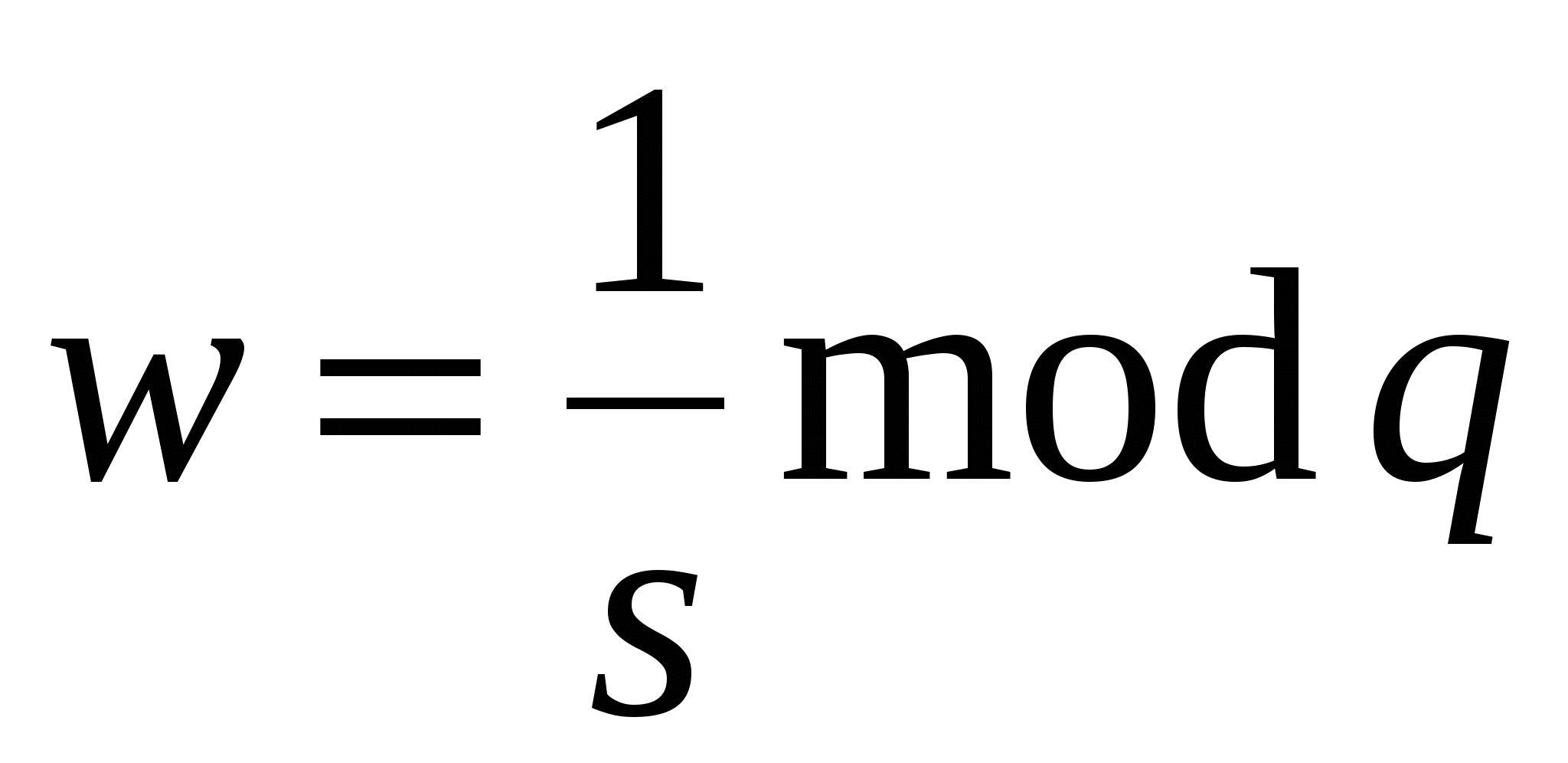 , ,
що не дозволяє добитися максимальної швидкодії.
Слід відмітити, що реальне виконання алгоритму DSA може бути прискорене за допомогою виконання попередніх обчислень. Зазначимо, що значення r не залежить від повідомлення М та його хеш-значення m. Тому можна заздалегідь створити набір випадкових значень К і для кожного з них обчислити значення r. Можна також заздалегідь обчислити обернені значення К-1 для кожного із значень К. Потім при надходженні повідомлення М, можна обчислити значення s для даних значень r та К-1. Такі попередні обчислення значно прискорюють роботу алгоритму DSA.
Цифрові підписи з додатковими функціональними можливостями. Розглянуті в цьому пункті цифрові підписи володіють додатковими функціональними властивостями, крім звичайних властивостей автентифікації повідомлення та неможливості відмови особи, яка підписала повідомлення від обов’язків, пов’язаних із підписаним документом. У більшості випадків вони об’єднують базову схему цифрового підпису, наприклад на основі алгоритму RSA, зі спеціальним протоколом, який забезпечує досягнення тих додаткових властивостей, якими базова схема цифрового підпису не володіє. До схем цифрового підпису з додатковими функціональними властивостями відносяться [Error: Reference source not found]:
схеми сліпого (blind) підпису;
схеми незаперечного (undeniable) підпису.
Схеми сліпого підпису. На відміну від звичайних схем цифрового підпису, схеми сліпого підпису (іноді називають схемами підпису всліпу) є двохсторонніми протоколами між відправником А та стороною В, що підписує документ. Розглянемо головну ідею цих схем. Відправник А посилає порцію інформації стороні В, яку В підписує і повертає А. Використовуючи отриманий підпис, сторона А може вирахувати підпис сторони В на важливому для себе повідомленні m. По завершенні цього протоколу сторона В нічого не знає ні про повідомлення m, ні про підпис під цим повідомленням. Мета сліпого підпису полягає в тому, щоб перешкодити підписуючій особі В ознайомитися з повідомленням сторони А, яке вона підписує, і з відповідним підписом під цим повідомленням. Тому в подальшому підписане повідомлення неможливо зв’язати зі стороною А.
Розглянемо приклад використання сліпого підпису. Схема сліпого підпису може знайти застосування в тих випадках, коли відправник А (клієнт банку) не хоче, щоб підписуюча сторона В (банк) мала можливість в подальшому зв’язати повідомлення m та підпис sB(m) з певним кроком виконаного раніше протоколу. Зокрема це може бути важливим для організації анонімних безготівкових розрахунків, коли повідомлення m могло б представляти грошову суму, яку А хоче витратити. Коли повідомлення m з підписом sB(m) надається банку В для оплати, банк В не може прослідкувати, хто саме із клієнтів надає підписаний документ. Це дозволяє користувачу А залишитися анонімним. Цей метод використовується при організації системи анонімних безготівкових розрахунків із застосуванням „електронних грошей“.
Для побудови протоколу сліпого підпису необхідні наступні компоненти [Error: Reference source not found]:
Механізм звичайного цифрового підпису для підписуючої сторони В. Нехай sB(Х) позначає підпис сторони В на документі Х.
Функції f() та g() (відомі тільки відправнику) такі, що
g(sB(f(m)))=sm(m),
де f() – маскуюча (blinding) функція; g() – демаскуюча (unblinding) функція; f(m) – замасковане (blinded) повідомлення m.
При виборі sB, f та g існує ряд обмежень.
Виберемо в якості алгоритму підпису sB для сторони В схему цифрового підпису RSA з відкритим ключем (N,E) та секретним ключем D, причому N=P*Q – добуток двох великих випадкових простих чисел. Нехай k – деяке фіксоване ціле число, взаємно просте з N (НСД(N,k)=1). Маскуюча функція f:Zn→Zn визначається як f(m)=m*kE modN, а демаскуюча функція g:Zn→Zn – як g(m)=k-1m modN. При такому виборі f,g та s отримуємо
g(sB(f(m)))=g(sB(mkE modN))=g(mDk modN=mD modN=sB(m),
що відповідає наведеній вище вимозі 2.
Згідно з протоколом сліпого підпису, який запропонував Д. Чом [Error: Reference source not found], відправник А спочатку отримує підпис сторони В на замаскованому повідомленні m. Використовуючи цей підпис, сторона А обчислює підпис В на заздалегідь вибраному повідомленні m, де 0≤m≤N-1. При цьому стороні В нічого не відомо ні про значення m, ні про підпис, зв’язаний з m. Нехай сторона В має для підпису за схемою RSA відкритий ключ (N,E) та секретний ключ D. Нехай k – випадкове секретне ціле число, вибране стороною А і таке, що задовольняє умовам 0≤k≤N-1 та НСД(N,k)=1. Протокол сліпого підпису Д. Чома включає наступні кроки:
Відправник А обчислює замасковане повідомлення m*=mkE modN та відправляє його стороні В.
Підписуюча сторона В обчислює підпис s*=(m*)D modN та відправляє цей підпис стороні А.
Сторона А обчислює підпис s=k-1s* modN, який є підписом В на повідомленні m.
Нескладно побачити, що
(m*)D(mkE)DmDk (modN),
тому
k-1s*mDkk-1mD (modN).
Д. Чом розробив декілька алгоритмів сліпого незаперечуваного підпису для створення системи анонімних безготівкових електронних розрахунків eCash.
Системи незаперечного підпису. Незаперечуваний підпис, як і звичайний цифровий підпис, залежить від підписаного документу та секретного ключа. Проте, на відміну від звичайних цифрових підписів, незаперечуваний підпис не може бути верифікований без участі особи, що поставила цей підпис. Розглянемо два можливі сценарії застосування незаперечуваного підпису.
Сценарій 1. Сторона А (клієнт) хоче отримати доступ до захищеної зони, яка контролюється стороною В (банком). Цією захищеною зоною може бути, наприклад, депозитарій (сховище цінностей клієнтів). Сторона В вимагає від А поставити до надання клієнту доступу на заявці про допуск у захищену зону підпис, час та дату. Якщо А застосує незаперечуваний підпис, тоді сторона В не зможе у майбітньому довести будь-кому, що А отримав допуск без безпосередньої участі А у процесі верифікації підпису.
Сценарій 2. Нехай відома корпорація А розробила пакет програмного забезпечення. Для гарантування автентичності пакету та відсутності у ньому вірусів, сторона А підписує цей пакет незаперечуваним підписом та продає його стороні В. Сторона В вирішує зробити копії цього пакету програмного забезпечення і перепродати його третій стороні С. При використання стороною А незаперечуваного підпису сторона С не зможе впевнитися в автентичності цього пакету програмного забезпечення та відсутності в ньому вірусів без участі сторони А. Цей сценарій, звичайно, не перешкоджає стороні В поставити на пакеті свій підпис, але тоді для сторони В будуть втрачені усі маркетингові переваги, пов’язані з використанням торгової марки корпорації А. Крім того буде легше розкрити шахрайську діяльність сторони В.
Розглянемо алгоритм незаперечуваного цифрового підпису, розроблений Д. Чомом [Error: Reference source not found]. Спочатку опишемо алгоритм генерації ключів, за допомогою якого кожна сторона А, що підписує документ, вибирає секретний ключ та відповідний йому відкритий ключ. Кожна сторона А повинна виконати наступне:
Вибрати випадкове просте число p=2q+1, де q – також просте число.
Вибрати генераторне число для підгрупи порядку q в циклічній групі Zp*:
Вибрати випадковий елемент Zp та обчислити =(p-1)/q modp.
Якщо =1, тоді повернутися до кроку 2.1.
Вибрати випадкове ціле х{1,2,...,q-1} і обчислити y=x modp.
Для сторони А відкритий ключ рівний (p,,y), секретний ключ рівний х.
Згідно алгоритму незаперечуваного підпису Д. Чома, сторона А підписує повідомлення m, що належить підгрупі порядку q в Zp*. Будь-яка сторона В може перевірити цей підпис за участі А.
В роботі алгоритму незаперечуваного підпису можна виділити два етапи:
генерація підпису;
верифікація підпису.
На етапі генерації підпису сторона А обчислює s=mx modp, де s – підпис сторони А на повідомленні m. Повідомлення m з підписом s відсилається стороні В. Етап верифікації підпису виконується стороною В за участі сторони А та включає наступні кроки:
В отримує справжній ключ (p,,y) сторони А.
В вибирає два випадкових секретних цілих числа а, b {1,2,...,q-1}.
В обчислює z=sayb modp та відправляє значення z стороні А.
А обчислює w=(z)1/xmodp, де xx-11(modq), і відправляє значення w стороні В.
В обчислює w'=mab modp і визнає підпис s справжнім, якщо і тільки якщо w=w'.
Впевнимося, що перевірка підпису s працює:
w(z)1/x(sayb)1/x(mxaxb)1/xmabw' modp.
Можна довести, що з високою ступінню ймовірності зловмисник не зможе заставити В прийняти фальшивий підпис. Припустимо, що s являє собою підроблений підпис сторони А на повідомленні m (s≠mx modp). Тоді ймовірність прийняття цього підпису в даному алгоритмі складає тільки 1/q, причому ця ймовірність не залежить від обчислювальних ресурсів зловмисника.
Сторона А, яка підписала повідомлення, за деяких обставин могла б відмовитися від свого справжнього підпису одним з трьох способів:
відмовитися від участі у протоколі верифікації;
некоректно виконати протокол верифікації;
оголосити підпис фальшивим, навіть якщо протокол верифікації виявився успішним.
Відмова від підпису першим способом розглядалася б як очевидна спроба неправомірної відмови. Проти другого та третього способів боротися складніше – тут потрібен спеціальний протокол дезавуювання. Цей протокол визначає, чи пробує сторона А дезавуювати правильний підпис s чи цей підпис є фальшивим. В цьому протоколі по суті двічі застосовується протокол верифікації і потім здійснюється перевірка з метою впевнитися, що сторона А виконує цей протокол коректно.
Протокол дезавуювання для схеми незаперечуваного підпису Д. Чома включає такі кроки:
В приймає від сторони А повідомлення m з підписом s та отримує справжній відкритий ключ (p,,y) сторони А.
B вибирає випадкові секретні цілі числа а, b {1,2,...,q-1}, обчислює z=sayb modp та відправляє значення z стороні А.
А обчислює , w=(z)1/xmodp, де xx-11(modq), і відправляє значення w стороні В.
Якщо w=mab modp, тоді В визнає підпис s справжнім і виконання протоколу зупиняється.
В вибирає випадкові секретні цілі числа а', b' {1,2,...,q-1}, обчислює z'=sa'yb' modp та відправляє значення z' стороні А.
А обчислює w'=(z')1/xmodp та відправляє значення w' стороні В.
Якщо w'=sa'yb' modp, тоді В приймає підпис s і виконання протоколу зупиняється.
В обчислює c=(w-b)a' modp, c'=(w'-b')a modp. Якщо c=c', тоді В впевнюється, що підпис s є фальшивим; в іншому випадку В робить висновок, що підпис s справжній, а сторона А робить спробу дезавуювати підпис s.
Нескладно впевнитися в тому, що цей протокол досягає поставленої мети. Нехай m – повідомлення, і нехай s – підпис сторони А під повідомленням m. Якщо підпис s фальшивий (s≠mx modp), і якщо сторони А та В правильно слідують протоколу, тоді w=w' (і тому справедливий висновок В, що підпис s є фальшивим). Нехай s насправді є підписом сторони А під повідомленням m (s=mx modp). Нехай В точно слідує протоколу, а А не слідує. Тоді ймовірність того, що w=w' (і А вдалося дезавуювати підпис), складає тільки 1/q.
Слід відмітити, що третя сторона С ніколи не повинна приймати в якості доказу справжності підпису s запис стороною В протоколу верифікації, оскільки сторона В може фальсифікувати успішний запис кроку 2 і наступних кроків протоколу верифікації без участі підписуючої сторони А. Незаперечуваний підпис може бути верифікований тільки шляхом безпосередньої взаємодії з підписуючою стороною А.
Також розроблено алгоритм для оборотного незаперечуваного підпису, який може бути верифікований, дезавуйований, а також перетворений у звичайний цифровий підпис. Цей алгоритм базується на використанні алгоритму цифрового підпису Ель Гамаля.
|
|
|
 Скачать 3.63 Mb.
Скачать 3.63 Mb.



