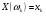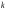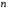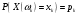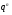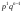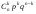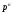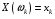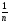Лекція 10. Біном. та норм.розподіли. Біноміальний, рівномірний і нормальний розподіл ймовірностей
 Скачать 0.87 Mb. Скачать 0.87 Mb.
|
|
Ю.Д.Жданова. Лекції з ВГПМ. М3 Вибрані глави ТЙіМС. Лекція № 10 Лекція № 10 Тема: Біноміальний, рівномірний і нормальний розподіл ймовірностей План лекції: 1. Біноміальний розподіл ймовірностей. 2. Рівномірний розподіл ймовірностей. 3. Нормальний розподіл ймовірностей. 4. Нормальне наближення. 5. Розподіли, пов’язані з нормальним. 6. Оцінки параметрів розподілу випадкових величин. 7. Оцінки параметрів біноміального розподілу. 8. Оцінки параметрів нормального розподілу. 1. Біноміальний розподіл ймовірностей Припустимо, що проводиться серія незалежних випробувань, в кожному з яких може відбутися подія 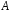 з однією і тією ж, але невідомою нам ймовірністю з однією і тією ж, але невідомою нам ймовірністю 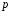 . Причому ймовірність появи події . Причому ймовірність появи події 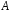 в кожному випробуванні не залежить від результатів інших випробувань. Такі випробування називаються незалежними відносно події в кожному випробуванні не залежить від результатів інших випробувань. Такі випробування називаються незалежними відносно події 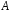 . Нехай проведено . Нехай проведено 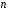 незалежних випробувань. Випадкова величина незалежних випробувань. Випадкова величина 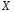 – число появ події – число появ події 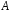 (появу події називають «успіхом») в цій серії випробувань. Можливими значеннями цієї випадкової величини є цілі числа від 0 до (появу події називають «успіхом») в цій серії випробувань. Можливими значеннями цієї випадкової величини є цілі числа від 0 до 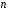 . Ймовірності цих можливих значень визначаються за формулою Бернуллі. Закон розподілу такої випадкової величини називається біноміальним. . Ймовірності цих можливих значень визначаються за формулою Бернуллі. Закон розподілу такої випадкової величини називається біноміальним. Означення. Дискретна випадкова величина 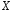 називається розподіленою за біноміальним законом, якщо її можливими значеннями називається розподіленою за біноміальним законом, якщо її можливими значеннями 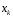 є числа успіхів є числа успіхів 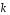 в схемі Бернуллі при в схемі Бернуллі при 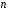 випробуваннях, а ймовірності знаходяться за формулою Бернуллі випробуваннях, а ймовірності знаходяться за формулою Бернуллі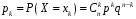 , , ( 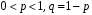 , , 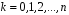 ). ).Закон розподілу:
Звернемо увагу на те, що сума ймовірностей 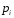 – це точно біном Ньютона – це точно біном Ньютона 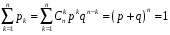 . .Цей факт і вплинув на назву випадкової величини, яка розглядається. Позначається біноміальний розподіл так: 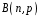 , де , де 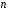 і і 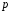 – параметри біноміального розподілу. – параметри біноміального розподілу.Функція розподілу: 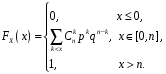 Числові характеристики: 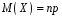 , , 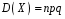 , , 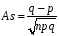 , , 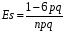 . .Найімовірніше значення 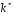 випадкової величини випадкової величини 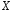 , розподіленої за біноміальним законом задовольняє нерівність: , розподіленої за біноміальним законом задовольняє нерівність: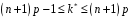 . .Приклад. На заліку студент отримав 4 задачі. Ймовірність правильно розв’язати кожну задачу 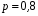 . Випадкова величина . Випадкова величина 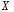 – число правильно розв’язаних задач. – число правильно розв’язаних задач. а) Знайти закон розподілу випадкової величини 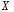 ; ;б) побудувати функцію розподілу випадкової величини 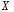 та її графік. та її графік.в) Знайти 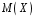 , , 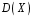 , , 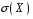 . .Розв’язання. а) Можливі значення випадкової величини 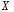 : 0,1,2,3,4. Оскільки можливими значеннями випадкової величини : 0,1,2,3,4. Оскільки можливими значеннями випадкової величини 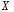 є числа успіхів є числа успіхів 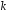 в схемі Бернуллі при 4 випробуваннях, то їх ймовірності знаходяться за формулою Бернуллі: в схемі Бернуллі при 4 випробуваннях, то їх ймовірності знаходяться за формулою Бернуллі: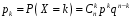 , , 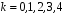 , , 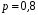 . .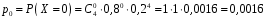 ; ;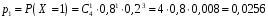 ; ;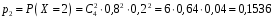 ; ;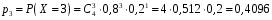 ; ;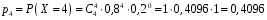 . .Закон розподілу запишемо у вигляді таблиці:
Перевірка умови нормування: 0,0016+0,0256+0,1536+0,4096+0,4096=1. Отже, випадкова величина 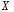 має біноміальний розподіл має біноміальний розподіл 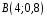 . . б) Функція розподілу випадкової величини 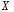 за означенням: за означенням: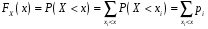 Компактно 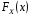 можна записати в такій формі: можна записати в такій формі: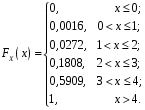 Графік функції 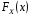 зображено на малюнку: зображено на малюнку:0 1 2 3 4 к 0,5 0,1 1 в) Знайдемо 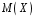 , , 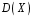 , , 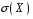 . .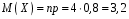 ; ;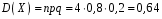 ; ;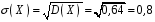 . .1.1. Розподіл Бернуллі Біноміальний розподіл 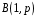 з параметрами з параметрами 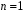 і і 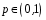 називається розподілом Бернуллі. називається розподілом Бернуллі. Числові характеристики: 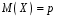 , , 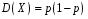 . .Розподіл Бернуллі 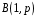 відіграє фундаментальну роль в теорії ймовірностей і математичний статистиці, являючись математичною моделлю випробування з двома наслідками. відіграє фундаментальну роль в теорії ймовірностей і математичний статистиці, являючись математичною моделлю випробування з двома наслідками.Якщо 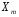 , , 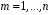 – незалежні випадкові величини з розподілом Бернуллі, тоді випадкова величина – незалежні випадкові величини з розподілом Бернуллі, тоді випадкова величина 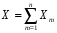 має біноміальний розподіл має біноміальний розподіл 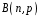 . .Приклад. Нехай в партії деяких виробів якісні вироби зустрічаються з ймовірністю 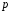 , а вироби з дефектом – з ймовірністю , а вироби з дефектом – з ймовірністю 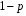 . Покладемо . Покладемо 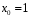 , якщо вибрали виріб якісний, і , якщо вибрали виріб якісний, і 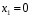 , якщо виріб з дефектом. Тоді «якість» виробів можна описати випадковою величиною, що має розподіл Бернуллі , якщо виріб з дефектом. Тоді «якість» виробів можна описати випадковою величиною, що має розподіл Бернуллі 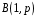 . .2. Рівномірний розподіл 2.1 Рівномірний дискретний розподіл Означення. Дискретна випадкова величина 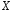 називається рівномірно розподіленою, якщо вона набуває називається рівномірно розподіленою, якщо вона набуває 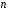 значень значень 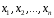 з ймовірностями з ймовірностями 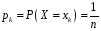 , , 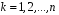 . .Закон розподілу:
Функція розподілу: 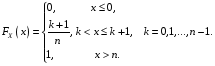 Числові характеристики: 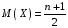 , , 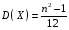 . .2.2 Рівномірний неперервний розподіл Означення. Неперервна випадкова величина 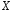 називається рівномірно розподіленою на відрізку називається рівномірно розподіленою на відрізку 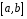 , якщо її щільність ймовірності є сталою на , якщо її щільність ймовірності є сталою на 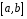 і дорівнює 0 поза ним: і дорівнює 0 поза ним: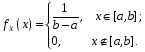 Графік функції 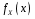 має вид: має вид:0 a b x  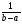 Рівномірний розподіл виникає в експериментах, у яких навмання ставиться точка на відрізку 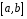 (випадкова величина (випадкова величина 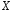 – абсциса поставленої точки), а також в експериментах по вимірюванню тих чи інших фізичних величин з округленням (випадкова величина – абсциса поставленої точки), а також в експериментах по вимірюванню тих чи інших фізичних величин з округленням (випадкова величина 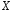 – помилка округлення). Наприклад: – помилка округлення). Наприклад: 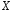 – час чекання на зупинці автобуса: – час чекання на зупинці автобуса: 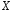 розподілена рівномірно на відрізку розподілена рівномірно на відрізку 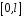 , де , де  – інтервал руху автобусів. Інший приклад: – інтервал руху автобусів. Інший приклад: 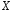 – помилка при зважуванні предмета, яка отримана від округлення результату зважування до найближчого цілого числа; у цьому випадку випадкова величина – помилка при зважуванні предмета, яка отримана від округлення результату зважування до найближчого цілого числа; у цьому випадку випадкова величина 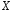 має рівномірний розподіл на відрізку має рівномірний розподіл на відрізку 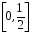 , де за одиницю прийнята ціна розподілу шкали. , де за одиницю прийнята ціна розподілу шкали.Функція розподілу: 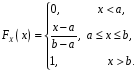 Числові характеристики: 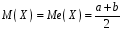 , , 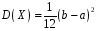 , , 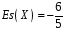 . .3. Нормальний розподіл ймовірностей Означення. Неперервна випадкова величина 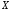 називається розподіленою за нормальним законом (законом Гаусса) з параметрами називається розподіленою за нормальним законом (законом Гаусса) з параметрами 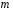 і і 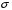 , де , де 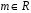 , , 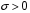 , якщо її щільність ймовірності має вигляд: , якщо її щільність ймовірності має вигляд: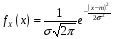 , , 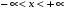 Нормальний розподіл було відкрито в 1733 році А. Муавром, а потім докладно вивчено П. Лапласом і К. Гауссом. Позначається нормальний розподіл 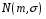 . .Якщо випадкова величина 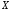 розподілена за нормальним законом розподілена за нормальним законом 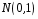 з параметрами 0 і 1, то вона називається нормованою або стандартною нормальною випадковою величиною. Щільність стандартного нормального розподілу є функцією Гаусса: з параметрами 0 і 1, то вона називається нормованою або стандартною нормальною випадковою величиною. Щільність стандартного нормального розподілу є функцією Гаусса: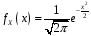 . .Зауваження. Для значень функції Гаусса існують детальні таблиці. Значення функції Гаусса можна обчислити а) в Excel за формулою =НОРМРАСП(х; 0;1;ЛОЖЬ). а) в Mathcad за формулою dnorm(x,0,1). Графік щільності нормального розподілу називається нормальною кривою (кривою Гаусса) і має наступний симетричний вигляд, схожий на дзвін; залежний від різних значень параметра 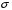 : :0 m x  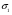 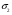 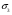 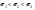 Максимальна висота дзвону досягається при 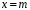 та дорівнює та дорівнює 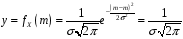 , ,При збільшенні параметра 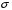 вершина дзвону буде опускатися, але зате будуть підніматися краї (тому що загальна площа між графіком і віссю вершина дзвону буде опускатися, але зате будуть підніматися краї (тому що загальна площа між графіком і віссю 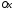 повинна залишитися рівною 1). Що стосується параметра повинна залишитися рівною 1). Що стосується параметра 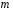 , то його значення не впливає на форму графіка; зі зміною , то його значення не впливає на форму графіка; зі зміною 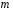 графік тільки зміщується в напрямку осі графік тільки зміщується в напрямку осі 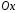 . .Нормальний закон – це закон розподілу, що найчастіше зустрічається на практиці. Він широко розповсюджений у природі, техніці виробництві, і т. ін.. Випадковими величинами з нормальним законом розподілу є, наприклад, погрішності вимірювань фізичних величин, та й самі результати вимірювань; координати точки падіння снаряда під час стрілянини з гармати при постійному прицілі й ін. Функція розподілу: 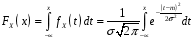 . .Функція розподілу нормальної випадкової величини зв'язана з функцією Лапласа наступним співвідношенням: 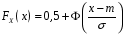 . .Зауваження. Для значень функції розподілу нормальної випадкової величини існують детальні таблиці. Значення функції цієї функції можна обчислити а) в Excel за формулою =НОРМРАСП(х; 0;1;ИСТИНА)–0,5 або за формулою =НОРМСТРАСП(х)–0,5. а) в Mathcad за формулою pnorm(x,0,1)–0,5. Ймовірність того, що нормально розподілена випадкова величина набуває значень з деякого проміжку 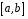 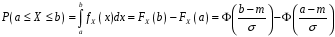 . .Якщо покласти 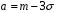 , , 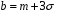 , то , то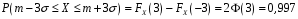 , ,тобто подія 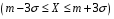 є практично достовірною. Це означає, що практично всі можливі значення нормально розподіленої випадкової величини розташовані на проміжку є практично достовірною. Це означає, що практично всі можливі значення нормально розподіленої випадкової величини розташовані на проміжку 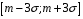 . Останнє твердження називають "правилом трьох сигм". . Останнє твердження називають "правилом трьох сигм".Числові характеристики нормального розподілу збігаються з його параметрами: 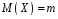 , , 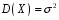 , , 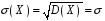 . .Нормальний розподіл має широке розповсюдження в прикладних задачах. Це пов’язано з тим, що багато з випадкових величин, які досліджуються, є наслідками різних випадкових подій. Зокрема, при достатньо загальних припущеннях сума великого числа незалежних випадкових величин має розподіл, близький до нормального. |