Лекція 10. Біном. та норм.розподіли. Біноміальний, рівномірний і нормальний розподіл ймовірностей
 Скачать 0.87 Mb. Скачать 0.87 Mb.
|
|
8.4. Довірчий інтервал для дисперсії при невідомому математичному сподіванні Знайдемо довірчий інтервал для дисперсії 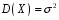 нормально розподіленої величини нормально розподіленої величини 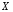 з невідомими математичним сподіванням. При виведенні інтервальної оцінки у разі відомого математичного сподівання , ми користувалися величиною з невідомими математичним сподіванням. При виведенні інтервальної оцінки у разі відомого математичного сподівання , ми користувалися величиною 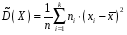 . Тепер це значення використовувати неможна, тому за незміщену оцінку дисперсії будемо використовувати виправлену вибіркову дисперсію . Тепер це значення використовувати неможна, тому за незміщену оцінку дисперсії будемо використовувати виправлену вибіркову дисперсію 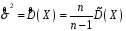 .. Випадкова величина .. Випадкова величина 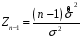 має розподіл Пірсона має розподіл Пірсона 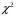 із із 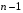 ступенями свободи. Виберемо близьку до одиниці ймовірність ступенями свободи. Виберемо близьку до одиниці ймовірність 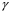 і знайдемо інтервал, в який потрапляє невідомий параметр з надійністю і знайдемо інтервал, в який потрапляє невідомий параметр з надійністю 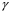 . Для цього повторимо міркування пункту 8.3 і отримаємо, що оцінюване значення дисперсії . Для цього повторимо міркування пункту 8.3 і отримаємо, що оцінюване значення дисперсії 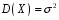 з надійністю з надійністю 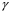 покривається довірчим інтервалом покривається довірчим інтервалом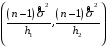 . .Приклад 5. В умовах прикладу 3 знайти довірчий інтервал для дисперсії 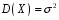 при невідомому математичному сподіванні з надійністю при невідомому математичному сподіванні з надійністю 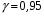 . . Розв’язання. Об'єм вибірки 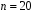 , вибіркове середнє , вибіркове середнє 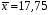 , вибіркова дисперсія , вибіркова дисперсія 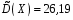 , виправлена вибіркова дисперсія , виправлена вибіркова дисперсія 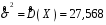 . .Отримаємо довірчий інтервал для дисперсії: 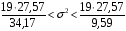 , ,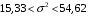 . .Таким чином, інтервал 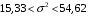 покриває параметр покриває параметр 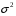 з надійністю з надійністю 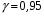 при невідомому математичному сподіванні. при невідомому математичному сподіванні.8.5. Довірчий інтервал для середнього квадратичного відхилення Нехай генеральна сукупність випадкової величини 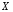 розподілена нормально. Треба оцінити невідоме генеральне середнє квадратичне відхилення розподілена нормально. Треба оцінити невідоме генеральне середнє квадратичне відхилення 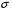 за виправленим середнім квадратичним відхиленням за виправленим середнім квадратичним відхиленням 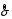 . Для цього знайдемо довірчий інтервал, що покриває невідомий параметр . Для цього знайдемо довірчий інтервал, що покриває невідомий параметр 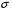 з надійністю з надійністю 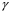 . По суті, ця задача повторює попередній пункт, але зараз ми трохи змінимо позначення для спрощення запису результату. . По суті, ця задача повторює попередній пункт, але зараз ми трохи змінимо позначення для спрощення запису результату. Вираз для довірчої ймовірності має вигляд 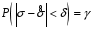 , де , де 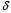 – абсолютна похибка оцінювання. Нерівність – абсолютна похибка оцінювання. Нерівність 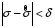 або рівносильну йому нерівність або рівносильну йому нерівність 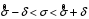 перетворимо до виду перетворимо до виду 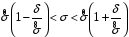 . Позначимо . Позначимо 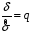 і, оскільки абсолютну похибку оцінювання ми вибираємо достатньо малою, можна вважати, що і, оскільки абсолютну похибку оцінювання ми вибираємо достатньо малою, можна вважати, що 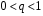 . Перепишемо нерівність у вигляді . Перепишемо нерівність у вигляді 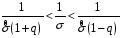 , домножимо на , домножимо на 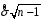 , отримаємо , отримаємо 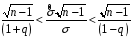 . З попереднього пункту відомо, що випадкова величина . З попереднього пункту відомо, що випадкова величина 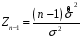 має розподіл Пірсона має розподіл Пірсона 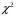 із із 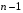 ступенями свободи. Тому змінну ступенями свободи. Тому змінну 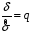 можна виразити через значення критичних точок можна виразити через значення критичних точок 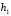 і і 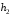 розподілу розподілу 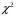 і записати ці значення в таблицю (у застосуваннях значення параметра і записати ці значення в таблицю (у застосуваннях значення параметра 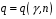 приведені в спеціальних статистичних таблицях). Вичисливши по вибірці значення приведені в спеціальних статистичних таблицях). Вичисливши по вибірці значення 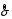 і знайшовши за таблицею і знайшовши за таблицею 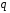 , отримаємо шуканий довірчий інтервал для середнього квадратичного відхилення, покриваючий параметр , отримаємо шуканий довірчий інтервал для середнього квадратичного відхилення, покриваючий параметр 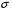 із заданою надійністю із заданою надійністю 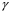 : : 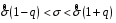 . .Зауваження. У випадках, коли оцінюється математичне сподівання при невідомій дисперсії або дисперсія при невідомому математичному сподіванні, довірчі інтервали, що виходять при цьому, виявляються довше за тих, що отримані, коли, відповідно, дисперсія або математичне сподівання були відомі. Ця обставина пояснюється тим, що наявність додаткової інформації дозволяє звузити межі, в які можна укласти оцінюваний параметр при заданій надійності. Приклад 6. В умовах прикладу 3 знайти довірчий інтервал для середнього квадратичного відхилення 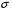 з надійністю з надійністю 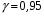 . . Розв’язання. Об'єм вибірки 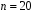 , вибіркове середнє , вибіркове середнє 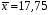 , вибіркова дисперсія , вибіркова дисперсія 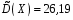 , виправлена вибіркова дисперсія , виправлена вибіркова дисперсія 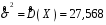 , виправлене вибіркове середнє квадратичне відхилення , виправлене вибіркове середнє квадратичне відхилення 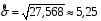 . . Довірчий інтервал для середнього квадратичного відхилення визначається нерівністю 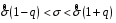 . .За заданою надійністю 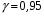 і об'ємом вибірки і об'ємом вибірки 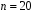 знайдемо за таблицями параметр знайдемо за таблицями параметр 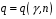 : : 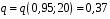 . Отримаємо довірчий інтервал для середнього квадратичного відхилення . Отримаємо довірчий інтервал для середнього квадратичного відхилення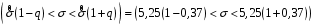 . .Проведемо обчислення і остаточно запишемо 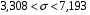 . .Таким чином, інтервал 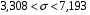 покриває параметр покриває параметр 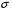 з надійністю з надійністю 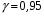 . . |
