Лекція 10. Біном. та норм.розподіли. Біноміальний, рівномірний і нормальний розподіл ймовірностей
 Скачать 0.87 Mb. Скачать 0.87 Mb.
|
|
4. Нормальне наближення Нехай випадкова величина 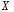 має біноміальний розподіл має біноміальний розподіл 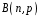 . .Якщо значення параметра 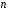 великі, то безпосереднє обчислення ймовірності подій, пов'язаних з цією випадковою величиною, технічно складно. В цих випадках можна використовувати наближення біноміального розподілу розподілом Пуассона і нормальним розподілом (наближення Муавра-Лапласа). великі, то безпосереднє обчислення ймовірності подій, пов'язаних з цією випадковою величиною, технічно складно. В цих випадках можна використовувати наближення біноміального розподілу розподілом Пуассона і нормальним розподілом (наближення Муавра-Лапласа). Наближення нормальним розподілом використовується в ситуаціях, коли 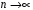 , а , а 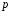 фіксовано. Це наближення можна розглядати як окремий випадок центральної граничної теореми, застосування якої засноване на представленні випадкової величини фіксовано. Це наближення можна розглядати як окремий випадок центральної граничної теореми, застосування якої засноване на представленні випадкової величини 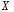 у вигляді суми доданків. Наближення засноване на тому, що за вказаних умов розподіл нормованої величини у вигляді суми доданків. Наближення засноване на тому, що за вказаних умов розподіл нормованої величини 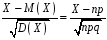 , де , де 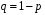 , ,близький до стандартного нормального. Локальна теорема Муавра-Лапласа Дана теорема використовується для наближеного обчислення ймовірностей окремих значень биноміального розподілу. Вона стверджує, що рівномірно по всім значенням 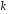 має місце має місце 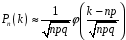 , ,де 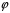 — щільність стандартного нормального розподілу, — щільність стандартного нормального розподілу, 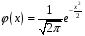 . (функція Гаусса.) . (функція Гаусса.)Інтегральна теорема Муавра-Лапласа На практиці необхідність оцінки ймовірності окремих значень, яку дає локальна теорема Муавра-Лапласа, виникає нечасто. Набагато більш важливо оцінювати ймовірність подій, що включають в себе множину значень. Для цього використовується інтегральна теорема, яку можна сформулювати в наступному виді: При 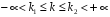 , і , і 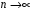 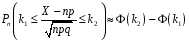 де 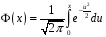 — функція розподілу стандартного нормального закону (функція Лапласа). — функція розподілу стандартного нормального закону (функція Лапласа).Відзначимо, що функція 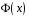 не залежить ні від яких параметрів. Отже, границя в теоремі Муавра-Лапласа є універсальною, оскільки вона не залежить від параметра, який є в дограничному виразі. Насправді, ця теорема є окремим випадком іншої, ще більше універсальної центральної граничної теореми. не залежить ні від яких параметрів. Отже, границя в теоремі Муавра-Лапласа є універсальною, оскільки вона не залежить від параметра, який є в дограничному виразі. Насправді, ця теорема є окремим випадком іншої, ще більше універсальної центральної граничної теореми.На практиці рішення про те, наскільки слід довіряти нормальному наближенню, приймають виходячи з величини 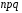 . Чим вона більша, тим менше буде погрішність наближення. . Чим вона більша, тим менше буде погрішність наближення. Помітимо, що асимптотичний результат не зміниться, якщо замінити нестрогі нерівності на строгі і навпаки. Гранична ймовірність від такої заміни також не зміниться, оскільки нормальний розподіл абсолютно неперервний і ймовірність набути будь-якого конкретного значення для нього дорівнює нулю. Проте початкова ймовірність від такої заміни може змінитися, що вносить у формулу деяку неоднозначність. Для великих значень 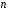 зміна буде невелика, проте для невеликих зміна буде невелика, проте для невеликих 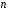 це може внести додаткову погрішність. це може внести додаткову погрішність. Для усунення цієї неоднозначності, а також підвищення точності наближення рекомендується задавати події, які нас цікавлять, у вигляді інтервалів з напівцілими межами. При цьому наближення виходить точніше. Це пов'язано з тим інтуїтивно зрозумілим міркуванням, що апроксимація кусково-сталої функції (функції розподілу біноміального закону) за допомогою неперервної функції дає точніші наближення між точками розриву, чим в цих точках. Приклад. Нехай 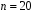 , , 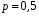 . Оцінимо ймовірність того, що число успіхів буде відрізнятися від найбільш ймовірного значення 10 не більше ніж на 3. Відзначимо, що значення . Оцінимо ймовірність того, що число успіхів буде відрізнятися від найбільш ймовірного значення 10 не більше ніж на 3. Відзначимо, що значення 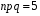 дуже мале, тому застосування нормального наближення тут досить ненадійно. дуже мале, тому застосування нормального наближення тут досить ненадійно. Точна ймовірність даної події дорівнює 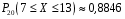 . .Застосуємо нормальне наближення з такою розстановкою нерівностей: (знизу строга, зверху нестрога): 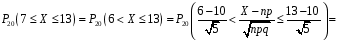 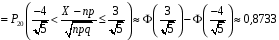 . .Помилка наближення дорівнює 0,8846–0,8733=0,0113. Тепер побудуємо наближення, використовуючи інтервал з кінцями в напівцілих точках: 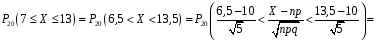 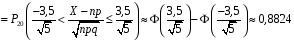 . .Помилка наближення дорівнює 0,8846–0,8724=0,0022 – приблизно в 5 разів менше, ніж в попередньому випадку. 5. Розподіли, пов’язані з нормальним За допомогою нормального розподілу визначаються три розподіли, які часто використовуються при статистичній обробці даних. Це розподіли Пірсона ("хі-квадрат"), Стьюдента і Фишера. 1) Розподіл 2 (хі-квадрат) Якщо кожна з незалежних випадкових величин 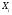 , , 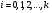 , характеризується стандартним нормальним законом розподілу ймовірностей , характеризується стандартним нормальним законом розподілу ймовірностей 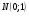 , то кажуть, що випадкова величина , то кажуть, що випадкова величина 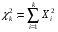 має розподіл має розподіл 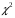 із із 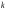 ступенями свободи із щільністю ймовірностей ступенями свободи із щільністю ймовірностей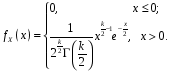 де 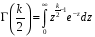 – гамма-функція Ейлера. – гамма-функція Ейлера.( 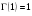 , , 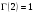 , , 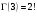 , , 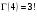 , і взагалі, , і взагалі, 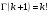 , , 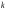 – може бути нецілим числом: – може бути нецілим числом: 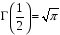 ) )Функція розподілу: 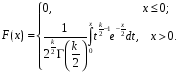 Розподіл 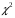 використовують при оцінюванні дисперсії (за допомогою довірчого інтервалу), при перевірці гіпотез узгодження, однорідності, незалежності, передусім для якісних змінних, що набувають скінченне число значень, і в багатьох інших задачах статистичного аналізу даних. використовують при оцінюванні дисперсії (за допомогою довірчого інтервалу), при перевірці гіпотез узгодження, однорідності, незалежності, передусім для якісних змінних, що набувають скінченне число значень, і в багатьох інших задачах статистичного аналізу даних.2) Розподіл Стьюдента (  -розподіл) -розподіл)Якщо випадкова величина 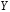 має стандартний розподіл має стандартний розподіл 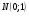 , а випадкова величина , а випадкова величина 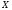 – розподіл – розподіл 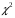 із із 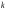 ступенями вільності, то величина ступенями вільності, то величина 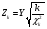 характеризується розподілом Стьюдента: характеризується розподілом Стьюдента: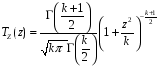 , , 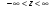 . .Функція розподілу: 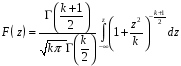 . . -розподіл, як і розподіл -розподіл, як і розподіл 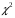 , має велике значення в математичній статистиці. , має велике значення в математичній статистиці.6. Оцінки параметрів розподілу випадкових величин Нехай 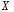 – спостережувана випадкова величина. Множина всіх можливих значень випадкової величини – спостережувана випадкова величина. Множина всіх можливих значень випадкової величини 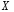 називається генеральною сукупністю. Вибірковою сукупністю або просто вибіркою називається множина називається генеральною сукупністю. Вибірковою сукупністю або просто вибіркою називається множина 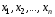 випадковим чином відібраних з генеральної сукупності об’єктів. Об’ємом сукупності (генеральної або вибіркової) називається число об’єктів цієї сукупності. випадковим чином відібраних з генеральної сукупності об’єктів. Об’ємом сукупності (генеральної або вибіркової) називається число об’єктів цієї сукупності.Характеристики і параметри спостережуваної випадкової величини називають генеральними, а їх оцінки, отримані за вибіркою, – вибірковими (наприклад, генеральна дисперсія і вибіркова дисперсія). Звичайно вибіркову оцінку позначають тою ж самою буквою, що і оцінюваний параметр, але їз знаком "" Нехай випадкова величина 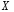 має функцію розподілу, яка залежить від має функцію розподілу, яка залежить від 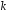 невідомих параметрів невідомих параметрів 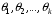 (параметрів розподілу, яких на практиці буває не більше чотирьох) (параметрів розподілу, яких на практиці буває не більше чотирьох) 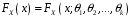 Необхідно за вибіркою 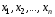 об’єму об’єму 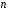 оцінити невідомі параметри оцінити невідомі параметри 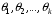 . . Означення. Оцінкою 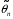 параметра параметра 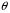 розподілу називається функція від вибірки розподілу називається функція від вибірки 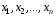 : :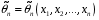 Інакше кажучи, оцінка параметра – це його наближене значення, отримане за вибіркою. Приклади оцінок. Вибіркове середнє 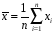 . .Вибіркова дисперсія 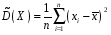 . .Властивості оцінок. 1. Оцінка 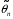 параметра параметра 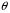 називається спроможною, якщо для будь-якого називається спроможною, якщо для будь-якого 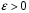 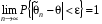 , ,тобто при збільшенні об’єму вибірки ( 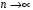 ) вона прямує до істинного значення параметра ) вона прямує до істинного значення параметра 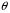 . .2. Оцінка 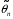 параметра параметра 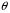 називається незміщеною (незміщена означає не зсунута відносно математичного сподівання), якщо називається незміщеною (незміщена означає не зсунута відносно математичного сподівання), якщо 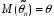 Незміщеність оцінки означає, що користуючись величиною 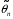 замість замість 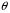 , ми не будемо робити систематичної помилки у бік завищення або заниження. , ми не будемо робити систематичної помилки у бік завищення або заниження.3. Оцінка 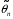 параметра параметра 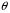 називається ефективною, якщо вона незміщена і у порівнянні з іншими оцінками має мінімальну дисперсію називається ефективною, якщо вона незміщена і у порівнянні з іншими оцінками має мінімальну дисперсію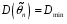 Вибіркова дисперсія 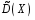 є спроможною і зміщеноюоцінкою генеральної дисперсії є спроможною і зміщеноюоцінкою генеральної дисперсії 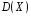 . За незміщену оцінку генеральної дисперсії беруть так звану виправлену дисперсію . За незміщену оцінку генеральної дисперсії беруть так звану виправлену дисперсію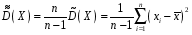 . .Існують наступні методи визначення точкових статистичних оцінок: 1) Метод умовних варіант. 2) Метод найменших квадратів 3) Метод моментів. 4) Метод максимальної правдоподібності. 7. Оцінки параметрів біноміального розподілу У цього розподілу два параметри: 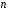 (число випробувань) і (число випробувань) і 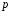 (ймовірність успіху в одному випробуванні). Часто зустрічається ситуація, коли (ймовірність успіху в одному випробуванні). Часто зустрічається ситуація, коли 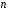 відоме, а відоме, а 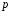 невідоме, тобто відоме число випробувань, але не відома ймовірність успіху в одному випробуванні. невідоме, тобто відоме число випробувань, але не відома ймовірність успіху в одному випробуванні.Для цього розподілу 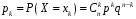 Точковою оцінкою 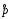 параметра параметра 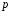 є є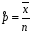 . .Особливо важливий окремий випадок, коли 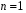 , в цьому випадку отримуємо , в цьому випадку отримуємо 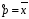 . Коли . Коли 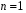 , , 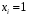 або або 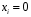 (успіх або невдача), тому (успіх або невдача), тому 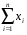 дорівнюватиме числу успіхів. Якщо позначити цю суму або число успіхів через дорівнюватиме числу успіхів. Якщо позначити цю суму або число успіхів через 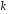 , отримаємо: , отримаємо: 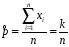 . .Оцінка 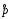 є незміщеною оцінкою параметра є незміщеною оцінкою параметра 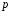 . .Приклад. Спортсмен вистрілив у ціль 20 разів, а влучив 15 разів. Визначити ймовірність влучення при одному пострілі. Розв’язання: 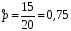 . .Знайдемо довірчий інтервал, який покриває невідомий параметр 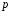 з надійністю з надійністю 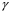 . Відомо, що біноміальний розподіл може бути наближений за допомогою нормального розподілу. Якщо оцінювана ймовірність не дуже мала і не дуже велика ( . Відомо, що біноміальний розподіл може бути наближений за допомогою нормального розподілу. Якщо оцінювана ймовірність не дуже мала і не дуже велика (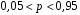 ), то можна вважати, що розподіл випадкової величини ), то можна вважати, що розподіл випадкової величини 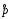 близький до нормального. Цим допущенням можна користуватися, якщо близький до нормального. Цим допущенням можна користуватися, якщо 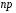 і і 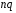 більше 4. Виберемо при заданій надійності більше 4. Виберемо при заданій надійності 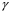 числа числа 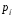 , , 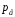 (нижню і верхню межу довірчого інтервала) так, щоб виконувалися нерівності (нижню і верхню межу довірчого інтервала) так, щоб виконувалися нерівності 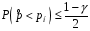 і і 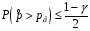 . Тоді ймовірність попадання значення . Тоді ймовірність попадання значення 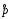 в інтервал ( в інтервал (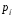 , , 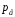 ) буде дорівнювати ) буде дорівнювати 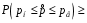 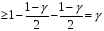 . Для практичного знаходження довірчих інтервалів з надійністю . Для практичного знаходження довірчих інтервалів з надійністю 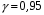 і і 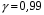 при при 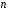 від 1 до 30, а також при від 1 до 30, а також при 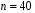 і і 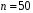 можна скористатися наперед складеними таблицями, які можна знайти в довідниках з математичної статистики. можна скористатися наперед складеними таблицями, які можна знайти в довідниках з математичної статистики. При великих об'ємах вибірки можна обійтися наближеною побудовою довірчого інтервалу. Скористаємося формулою ймовірності відхилення відносної частоти від постійної ймовірності в незалежних випробуваннях 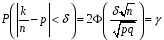 . .Позначимо 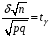 і, за допомогою таблиці значень функції Лапласа, розв’яжемо рівняння і, за допомогою таблиці значень функції Лапласа, розв’яжемо рівняння 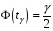 . З набутого значення . З набутого значення 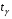 знайдемо знайдемо 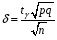 . Тоді . Тоді 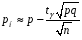 , , 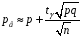 . Щоб отримати довірчий інтервал, треба виконати ще ряд перетворень, в результаті чого при великому об'ємі вибірки наближене значення для довірчого інтервалу має вид. . Щоб отримати довірчий інтервал, треба виконати ще ряд перетворень, в результаті чого при великому об'ємі вибірки наближене значення для довірчого інтервалу має вид.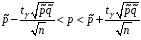 . .Приклад. При 20 пострілах спортсмен влучив у ціль 15 разів. Із надійністю 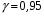 побудувати довірчий інтервал довірчий інтервал для ймовірності влучення при одному пострілі. побудувати довірчий інтервал довірчий інтервал для ймовірності влучення при одному пострілі.Розв’язання. Для побудови довірчого інтервалу необхідно знати: 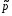 , , 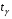 , , 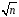 . З умови задачі маємо: . З умови задачі маємо: 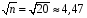 . Точкова оцінка ймовірності влучення знайдена в попередньому прикладі і дорівнює . Точкова оцінка ймовірності влучення знайдена в попередньому прикладі і дорівнює 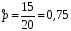 . .Величина 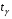 обчислюється з рівняння обчислюється з рівняння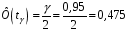 . .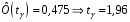 за таблицею значень функції Лапласа. за таблицею значень функції Лапласа.Знайдемо числові значення кінців довірчого інтервалу: 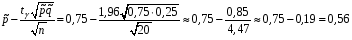 ; ;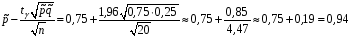 . .Таким чином, маємо: 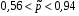 . .Отже, з надійністю 0,95 (95% гарантії) інтервал 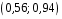 покриває оцінюваний параметр покриває оцінюваний параметр 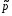 . .8. Оцінки параметрів нормального розподілу У цього розподілу два параметри: математичне сподівання 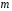 і дисперсія і дисперсія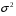 . Оцінками . Оцінками 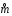 і і 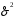 параметрів параметрів 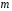 і і 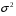 є є 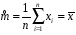 , , 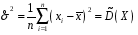 . .Величина 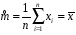 є незміщеною, спроможною і ефективною оцінкою математичного сподівання, тому її значення приймаємо за точкову оцінку значення математичного сподівання. є незміщеною, спроможною і ефективною оцінкою математичного сподівання, тому її значення приймаємо за точкову оцінку значення математичного сподівання. |
