Лекція 10. Біном. та норм.розподіли. Біноміальний, рівномірний і нормальний розподіл ймовірностей
 Скачать 0.87 Mb. Скачать 0.87 Mb.
|
|
8.1 Довірчий інтервал для математичного сподівання при відомій дисперсії Будемо вважати, що дисперсія 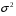 відома, тоді вибіркове середнє відома, тоді вибіркове середнє 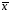 – нормально розподілена випадкова величина з параметрами – нормально розподілена випадкова величина з параметрами 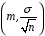 . Для такої випадкової величини ймовірність попадання на симетричний відносно математичного сподівання інтервал виражається через функцію Лапласа . Для такої випадкової величини ймовірність попадання на симетричний відносно математичного сподівання інтервал виражається через функцію Лапласа 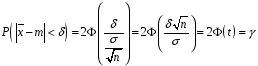 , ,де 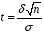 . При заданій надійності . При заданій надійності 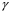 рівняння рівняння 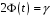 можна розв’язати наближено за допомогою таблиці значень функції Лапласа. можна розв’язати наближено за допомогою таблиці значень функції Лапласа. Якщо точного значення 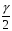 в таблиці значень немає, то потрібно знайти два найближчих до нього значення, одне більше, а інше менше, ніж в таблиці значень немає, то потрібно знайти два найближчих до нього значення, одне більше, а інше менше, ніж 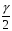 , і знайти їх середнє арифметичне. Відоме значення параметра , і знайти їх середнє арифметичне. Відоме значення параметра 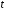 дозволяє записати абсолютну похибку дозволяє записати абсолютну похибку 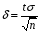 . Тепер можна вказати симетричний інтервал . Тепер можна вказати симетричний інтервал 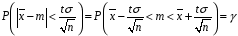 . Отримане співвідношення означає, що довірчий інтервал . Отримане співвідношення означає, що довірчий інтервал 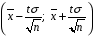 покриває невідомий параметр покриває невідомий параметр 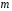 (математичне сподівання ) з ймовірністю (надійністю) (математичне сподівання ) з ймовірністю (надійністю) 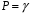 , а точність оцінки , а точність оцінки 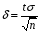 . .При фіксованому об'ємі вибірки з оцінки 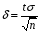 виходить, що чим більше довірча ймовірність, тим ширше межі довірчого інтервалу (тим більше помилка в оцінці математичного сподівання). Щоб знизити помилку в оцінці значення, можна збільшити об'єм вибірки. При цьому, щоб знизити відносну похибку на порядок, необхідно збільшити об'єм вибірки на два порядки. виходить, що чим більше довірча ймовірність, тим ширше межі довірчого інтервалу (тим більше помилка в оцінці математичного сподівання). Щоб знизити помилку в оцінці значення, можна збільшити об'єм вибірки. При цьому, щоб знизити відносну похибку на порядок, необхідно збільшити об'єм вибірки на два порядки.Приклад 1. За даними спостережень випадкової величини 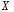 знайти довірчий інтервал для математичного сподівання знайти довірчий інтервал для математичного сподівання 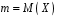 з надійністю з надійністю 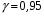 , якщо відома дисперсія , якщо відома дисперсія 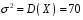 . Вибірка представлена таблицею. . Вибірка представлена таблицею.
Розв’язання. Знайдемо об'єм вибірки, для чого підсумуємо вказані в таблиці частоти: 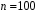 . Середнє вибіркове значення обчислимо за формулою . Середнє вибіркове значення обчислимо за формулою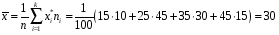 . .За заданою надійністю 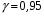 знайдемо, за допомогою таблиці, параметр знайдемо, за допомогою таблиці, параметр 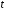 : : 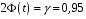 , звідки , звідки 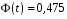 , , 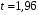 . Отримаємо довірчий інтервал для математичного сподівання . Отримаємо довірчий інтервал для математичного сподівання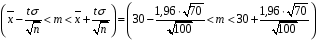 . .Проведемо обчислення і остаточно запишемо 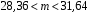 . .Таким чином, інтервал 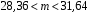 покриває параметр покриває параметр 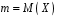 з надійністю з надійністю 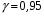 при відомій дисперсії при відомій дисперсії 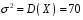 . .8.2 Довірчий інтервал для математичного сподівання при невідомій дисперсії У багатьох випадках припущення про нормальний розподіл випадкової величини 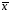 стає прийнятним при стає прийнятним при 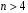 в цілому добре виправдовується при в цілому добре виправдовується при 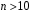 . Оцінка . Оцінка 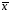 цілком придатна для застосування замість цілком придатна для застосування замість 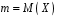 . Але все не так з дисперсією. Правомочність заміни . Але все не так з дисперсією. Правомочність заміни 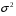 на вибіркову дисперсію на вибіркову дисперсію 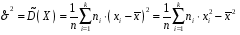 не обґрунтована навіть у вказаних випадках. При невеликому об'ємі вибірки, 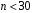 , закон розподілу оцінки дисперсії брати за нормальний невиправдано. Її розподіл слід апроксимувати розподілом хі-квадрат як суми квадратів центрованих величин (хі-квадрат розподіл збігається до нормального при числі доданків, що перевищує 30). Але це твердження обґрунтоване тільки тоді, коли випадкова величина Х розподілена нормально. , закон розподілу оцінки дисперсії брати за нормальний невиправдано. Її розподіл слід апроксимувати розподілом хі-квадрат як суми квадратів центрованих величин (хі-квадрат розподіл збігається до нормального при числі доданків, що перевищує 30). Але це твердження обґрунтоване тільки тоді, коли випадкова величина Х розподілена нормально.Розглянемо випадкові величини 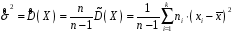 (виправлену вибіркову дисперсію – незміщену оцінку дисперсії 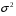 ) і ) і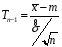 . .Тоді випадкова величина 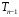 має розподіл Стьюдента з має розподіл Стьюдента з 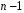 степенями вільності. Функція щільності розподілу цієї випадкової величини має вигляд степенями вільності. Функція щільності розподілу цієї випадкової величини має вигляд 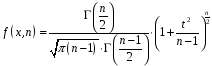 . .Розподіл Сьюдента симетричний, тому отримане співвідношення між точністю, надійністю оцінки і об’ємом вибірки зберігається. Виберемо число 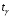 так, щоб виконувалась нерівність так, щоб виконувалась нерівність 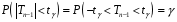 . .З означення функції щільності розподілу Стьюдента, значення меж інтервалу для параметра 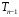 можна записати як розв’язок інтегрального рівняння можна записати як розв’язок інтегрального рівняння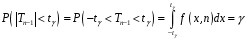 . .Розв’язок цього інтегрального рівняння позначається 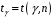 і наводиться в статистичних таблицях. і наводиться в статистичних таблицях.Зауваження. Критичні точки розподілу Стьюдента можна обчислити а) в Excel за формулою =СТЬЮДРАСПОБР(1-α; k), де α – рівень значущості ( 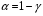 ), k – число ступенів свободи. ), k – число ступенів свободи. а) в Mathcad за формулою qt(1–α/2; k), де α – рівень значущості, k – число ступенів свободи. Приведемо нерівність 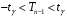 до еквівалентного вигляду до еквівалентного вигляду 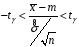 або 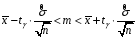 . .Ця нерівність задає довірчий інтервал для математичного сподівання 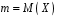 з надійністю з надійністю 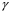 : :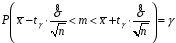 . .Приклад 2. В умовах прикладу 1 знайти довірчий інтервал для математичного сподівання 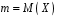 з надійністю з надійністю 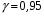 , якщо дисперсія невідома. , якщо дисперсія невідома. Розв’язання. Об'єм вибірки 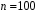 . Середнє вибіркове значення . Середнє вибіркове значення 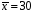 . Обчислимо вибіркову дисперсію: . Обчислимо вибіркову дисперсію: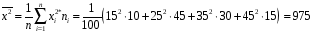 , ,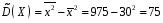 , ,і виправлену вибіркову дисперсію 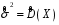 : : 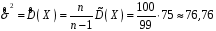 . .Об'єм заданої вибірки достатньо великий, 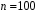 . Тому можна використовувати як розподіл Стьюдента, так і нормальний розподіл. Розглянемо обидва варіанти. . Тому можна використовувати як розподіл Стьюдента, так і нормальний розподіл. Розглянемо обидва варіанти.Варіант 1 (нормальний закон розподілу). Будемо припускати, що 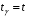 , а , а 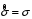 . За заданою надійністю . За заданою надійністю 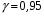 знайдемо за допомогою таблиці значень функції Лапласа, параметр знайдемо за допомогою таблиці значень функції Лапласа, параметр 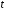 : : 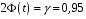 , звідки , звідки 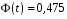 , , 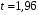 . Отримаємо довірчий інтервал для математичного сподівання . Отримаємо довірчий інтервал для математичного сподівання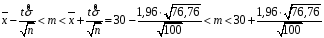 . .Проведемо обчислення і остаточно запишемо 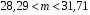 . .Таким чином, інтервал 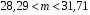 покриває параметр покриває параметр 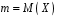 з надійністю з надійністю 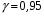 при невідомій дисперсії. при невідомій дисперсії.Варіант 2 (закон розподілу Стьюдента). За заданою надійністю 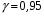 знайдемо за допомогою таблиці значень розподілу Стьюдента, параметр знайдемо за допомогою таблиці значень розподілу Стьюдента, параметр 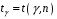 : : 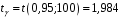 . Отримаємо довірчий інтервал для математичного сподівання . Отримаємо довірчий інтервал для математичного сподівання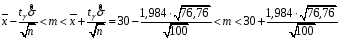 . .Проведемо обчислення і остаточно запишемо 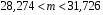 . .Таким чином, інтервал 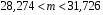 покриває параметр покриває параметр 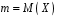 з надійністю з надійністю 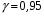 при невідомій дисперсії. при невідомій дисперсії.Можна помітити, що якщо значення 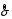 близьке до близьке до 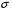 , то довірчий інтервал, отриманий із застосуванням закону розподілу Стьюдента, буде ширшим, ніж довірчий інтервал, отриманий із застосуванням формул нормального розподілу, оскільки , то довірчий інтервал, отриманий із застосуванням закону розподілу Стьюдента, буде ширшим, ніж довірчий інтервал, отриманий із застосуванням формул нормального розподілу, оскільки 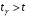 . Це пояснюється тим, що розподіл Стьюдента застосовується при вибірках малих об'ємів, що містять недостатній об'єм інформації. . Це пояснюється тим, що розподіл Стьюдента застосовується при вибірках малих об'ємів, що містять недостатній об'єм інформації.Приклад 3. За даними спостережень випадкової величини 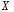 , розподіленої нормально, знайти довірчий інтервал для математичного сподівання , розподіленої нормально, знайти довірчий інтервал для математичного сподівання 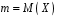 з надійністю з надійністю 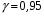 . Вибірка представлена таблицею. . Вибірка представлена таблицею.
Розв’язання. Знайдемо об'єм вибірки, для чого підсумуємо вказані в таблиці частоти: 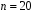 . Оскільки об'єм вибірки невеликий, то застосування нормального закону розподілу приведе до невиправданого звуження довірчого інтервалу, тому використовуємо формули, отримані для розподілу Стьюдента. Обчислимо необхідні параметри: . Оскільки об'єм вибірки невеликий, то застосування нормального закону розподілу приведе до невиправданого звуження довірчого інтервалу, тому використовуємо формули, отримані для розподілу Стьюдента. Обчислимо необхідні параметри: 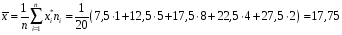 . .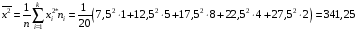 . .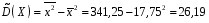 , ,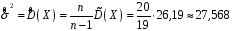 . .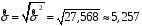 . .За заданою надійністю 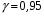 знайдемо за допомогою таблиці значень розподілу Стьюдента, параметр знайдемо за допомогою таблиці значень розподілу Стьюдента, параметр 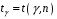 : : 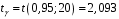 . Отримаємо довірчий інтервал для математичного сподівання . Отримаємо довірчий інтервал для математичного сподівання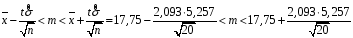 . .Проведемо обчислення і остаточно запишемо 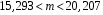 . .Таким чином, інтервал 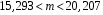 покриває параметр покриває параметр 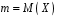 з надійністю з надійністю 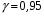 при невідомій дисперсії. при невідомій дисперсії.8.3. Довірчий інтервал для дисперсії при відомому математичному сподіванні Нехай 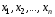 – вибірка спостережень з нормальної генеральної сукупності. Знайдемо довірчий інтервал для дисперсії – вибірка спостережень з нормальної генеральної сукупності. Знайдемо довірчий інтервал для дисперсії 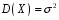 нормально розподіленої величини нормально розподіленої величини 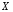 з відомими математичним сподіванням з відомими математичним сподіванням 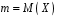 . .Оскільки значення математичного сподівання відоме, то як оцінку величини 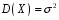 візьмемо точкову оцінку дисперсії візьмемо точкову оцінку дисперсії 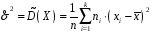 , яку будемо розглядати як випадкову величину, залежну від випадкової вибірки. Тоді величина , яку будемо розглядати як випадкову величину, залежну від випадкової вибірки. Тоді величина 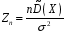 є сумою квадратів значень є сумою квадратів значень 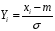 . Ці величини мають стандартний нормальний розподіл з параметрами 0 і 1, а сума . Ці величини мають стандартний нормальний розподіл з параметрами 0 і 1, а сума 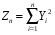 має має 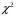 розподіл Пірсона з розподіл Пірсона з 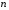 степенями вільності. Користуючись щільністю степенями вільності. Користуючись щільністю 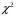 -розподілу, знайдемо інтервал, в який значення -розподілу, знайдемо інтервал, в який значення 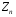 потрапляють з надійністю потрапляють з надійністю 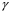 . Позначимо цей інтервал . Позначимо цей інтервал 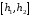 . Оскільки розподіл . Оскільки розподіл 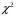 не є симетричним, то щоб отримати симетричний відносно параметра інтервал, значення не є симетричним, то щоб отримати симетричний відносно параметра інтервал, значення 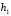 і і 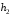 виберемо так, щоб ймовірність попадання значень виберемо так, щоб ймовірність попадання значень 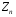 лівіше лівіше 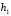 і правіше і правіше 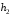 була однаково рівною була однаково рівною 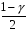 . Тоді . Тоді 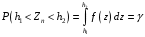 . .Числа 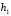 і і 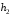 можна відшукати за спеціальною таблицею критичних точок розподілу можна відшукати за спеціальною таблицею критичних точок розподілу 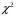 , виходячи з того, що , виходячи з того, що 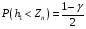 , , 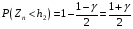 . Після того, як числа . Після того, як числа 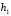 і і 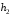 вибрані, можливо визначити довірчий інтервал для дисперсії вибрані, можливо визначити довірчий інтервал для дисперсії 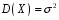 . Оскільки . Оскільки 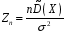 , то нерівність , то нерівність 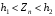 перетвориться на нерівність перетвориться на нерівність 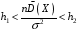 або, в еквівалентному вигляді або, в еквівалентному вигляді 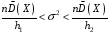 . Ця подвійна нерівність означає, що довірчим інтервалом для дисперсії . Ця подвійна нерівність означає, що довірчим інтервалом для дисперсії 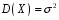 з надійністю з надійністю 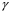 є проміжок є проміжок 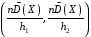 . .Зауваження. Таблиці критичних точок 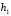 і і 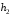 розподілу розподілу 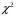 містять два параметри: рівень значущості містять два параметри: рівень значущості 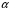 , визначуваний значеннями , визначуваний значеннями 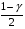 і і 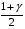 , а також число степенів свободи, рівне об'єму вибірки , а також число степенів свободи, рівне об'єму вибірки 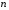 . Критичні значення в таблицях найчастіше позначаються . Критичні значення в таблицях найчастіше позначаються 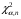 . . Зауваження. Критичні точки розподілу 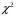 можна обчислити можна обчислити а) в Excel за формулою =ХИ2ОБР(α; k), де α – рівень значущості, k – число ступенів свободи. а) в Mathcad за формулою qchisq(1–α; k), де α – рівень значущості, k – число ступенів свободи. Приклад 4. В умовах прикладу 3 знайти довірчий інтервал для дисперсії 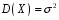 з надійністю з надійністю 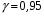 . . Розв’язання. Об'єм вибірки 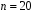 , вибіркове середнє , вибіркове середнє 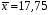 , вибіркова дисперсія , вибіркова дисперсія 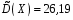 . За заданою надійністю . За заданою надійністю 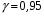 обчислимо обчислимо 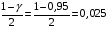 , , 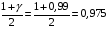 . .Відшукаємо числа 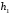 і і 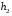 за таблицею критичних точок розподілу за таблицею критичних точок розподілу 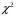 : :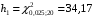 , , 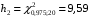 . .Отримаємо довірчий інтервал для дисперсії: 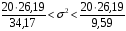 , ,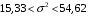 . .Таким чином, інтервал 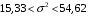 покриває параметр покриває параметр 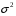 з надійністю з надійністю 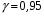 при відомому математичному сподіванні. при відомому математичному сподіванні. |