Регрессия с огр. коэф. Белорусский государственный университет экономический факультет
 Скачать 161.22 Kb. Скачать 161.22 Kb.
|
 МИНИСТЕРСТВО ОБРАЗОВАНИЯ РЕСПУБЛИКИ БЕЛАРУСЬ МИНИСТЕРСТВО ОБРАЗОВАНИЯ РЕСПУБЛИКИ БЕЛАРУСЬБЕЛОРУССКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ЭКОНОМИЧЕСКИЙ ФАКУЛЬТЕТ Кафедра аналитической экономики и эконометрики РЕГРЕССИЯ С ОГРАНИЧЕНИЯМИ НА КОЭФФИЦИЕНТЫ Курсовая работа Поуха Игнатия Юрьевича Студента 3 курса специальности «Экономика» очной формы получения высшего образования Научный руководитель: доцент, кандидат физико-математических наук Писарук Н.Н. Минск, 2016 ОГЛАВЛЕНИЕ Введение 3
Заключение 18 Список используемой литературы 19 ВВЕДЕНИЕ Рыночная экономика, несмотря на высокую степень способности к саморегулированию, предполагает целенаправленное внешнее воздействие на механизм собственного функционирования со стороны всех субъектов рыночных экономических взаимоотношений, которыми могут выступать отдельный индивид, предприятие и государство. В современных усло виях экономические прогнозы необходимы для определения возмож ных целей развития общества и обеспечивающих их достижение экономических ресурсов, для выявления наиболее вероятных и эко номически эффективных вариантов долгосрочных, среднесрочных и текущих планов, обоснования основных направлений экономической политики, предвидения последствий принимаемых ре шений. Одним, из важных направлений прогнозирования общественного развития является экономическое прогнозирование – научная эко номическая дисциплина. В ее распоряжении имеются многочисленные модели, с той или иной степенью достоверности описывающие реальную экономическую динамику. При этом исключительную роль в прогнозировании играет обработка статистических данных, анализ огромных массивов информации о социально-экономических явлениях и процессах. Всесторонний и глубокий анализ этой информации, так называемых статистических данных, предполагает использование различных специальных методов, важное место среди которых занимает корреляционный и регрессионный анализы обработки статистических данных. Корреляционный анализ применяется для измерения тесноты связи и оценивания факторов, которые оказывают наибольшее влияние. Регрессионный анализ – метод моделирования измеряемых данных и исследования их свойств. Регрессионный анализ необходим для выбора формы связи и типа модели, чтобы определить расчетные значения зависимой переменной (результата). Основы Теории РЕГРЕССИОННого АНАЛИЗаПри анализе экономических явлений на основе экономико-математических методов особое место занимают модели, выявляющие количественные связи между изучаемыми показателями и влияющими на них факторами. Научной дисциплиной, предмет которой составляет изучение этой количественной стороны экономических явлений и процессов средствами математического и статистического анализа, является эконометрика, в которой результаты теоретического анализа экономики синтезируются с выводами математики и статистики. Экономико-математическая модель факторного анализа, эконометрическая модель, служит главным инструментом эконометрики. Её параметры оцениваются средствами математической статистики. Эта модель выступает в качестве средства анализа и прогнозирования конкретных экономических процессов на основе реальной статистической информации. Например, экономические показатели функционирования предприятия (отрасли, хозяйства). Они как правило, представляются таблицами статистических данных:
Обычно один из экономических показателей выделяется в качестве результирующего и изучается влияние на него других показателей как факторов. Статистические данные представляют собой выборку некоторой реализации значений случайных величин: y(i) – i-ая реализация численного значения результата y, 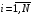 ; ; xj(i) – i-ая реализация численного значения j-ого фактора x, 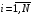 , ,  . .Использование статистических данных позволяет добиваться оптимальных результатов, управляя величинами факторов, или прогнозировать возможную величину результата при сложившихся значениях факторов. Между случайной величиной результата 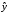 и случайной величиной фактора и случайной величиной фактора  имеется стохастическая (случайная) зависимость, т.е. существует корреляционная зависимость. имеется стохастическая (случайная) зависимость, т.е. существует корреляционная зависимость. Использование представленных в табличной форме статистических данных для выработки управленческих решений или прогнозов недостаточно удобно из-за их большого объема, ненаглядности и необходимости дополнительной обработки. Поэтому стремятся представить такие статистические данные в виде аналитической зависимости результата от факторов. Таким образом, корреляционную зависимость результата от факторов, проявляющуюся приблизительно и лишь в массе наблюдений, требуется отобразить с помощью функциональной зависимости результата от факторов, проявляющуюся определенно и точно в каждом конкретном случае. Задача состоит в определении интересующей нас случайной величины результата, если случайные величины факторов, от которых статистически зависит результат, приняли конкретные значения. Функциональная зависимость результата от факторов представляется уравнением регрессии. Различают уравнения (модели) парной и множественной регрессии. Парная корреляция выражается зависимостью между двумя случайными величинами – результатом и одним фактором: 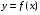 . (1.1) . (1.1)Множественная корреляция характеризует стохастическую связь между результатом и несколькими факторами:  . (1.2) . (1.2)Замена корреляционной зависимости на функциональную может привести к искажению отображения влияния факторов на результат. Поэтому общая задача регрессионного анализа состоит в определении такого вида и параметров уравнения регрессии, при которых наиболее точно представляется корреляционная зависимость. Одним из часто применяемых видов нелинейных многофакторных регрессионных моделей являются производственные функции. Стоить отметить, что параметры моделей парной и множественной регрессии находятся на основе метода наименьших квадратов. Метод наименьших квадратов (МНК) может быть использован для расчета коэффициентов только линейного уравнения регрессии.
При определении коэффициентов однофакторного уравнения регрессии с помощью табличных (фактических) значений определяют регрессионные остатки, характеризующие отклонения (ошибки), с которыми линейное уравнение регрессии отображает табличную функцию:  , ,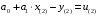 , (1.3) , (1.3) 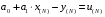 . .Ясно, что чем лучше будут подобраны коэффициенты линейного уравнения регрессии, тем меньше по абсолютной величине будут отклонения. Поэтому требуется найти такие значения коэффициентов a0 и a1, при которых сумма квадратов регрессионных остатков была бы минимальной: 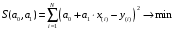 . (1.4) . (1.4)Функция двух аргументов S(a0, a1) принимает экстремальное значение, в данном случае минимальное, в точке (a0, a1), в которой частные производные этой функции по каждому аргументу равны нулю:  , , . (1.5) . (1.5)После преобразования получаем систему уравнений: 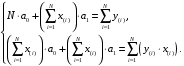 (1.6) (1.6)Решая систему двух линейных уравнений относительно двух неизвестных a0 и a1, определяются коэффициенты (параметры) линейного уравнения регрессии:  . (1.7) . (1.7)Аналогично рассчитываются коэффициенты многофакторного уравнения регрессии. Процесс построения и использования эконометрических моделей является достаточно сложным и включает в себя следующие основные этапы: определение цели исследования, построение системы показателей и логический отбор факторов, наиболее влияющих на каждый показатель; выбор формы связи изучаемых показателей между собой и отобранными факторами, другими словами, выбор типа эконометрической модели; сбор исходных данных и анализ информации; построение эконометрической модели, т.е. определение ее параметров; проверка качества построенной модели, в первую очередь ее адекватности изучаемому экономическому процессу; использование модели для экономического анализа и прогнозирования. При практической реализации указанных этапов очень важным является построение системы показателей исследуемого экономического процесса и определение перечня факторов, влияющих на каждый показатель. Укажем основные требования, предъявляемые к включаемым в эконометрическую модель факторам.
При отборе влияющих факторов используются статистические методы отбора. Так, существенного сокращения числа влияющих факторов можно достичь с помощью пошаговых процедур отбора переменных. Ни одна из этих процедур не гарантирует получения оптимального набора переменных. Однако при практическом применении они позволяют получать достаточно хорошие наборы существенно влияющих факторов; кроме того, их можно сочетать с другими подходами к решению данной проблемы, например с экспертными оценками значимости факторов. Среди пошаговых процедур отбора факторов наиболее часто используются процедуры пошагового включения и исключения факторов. Обе эти процедуры хорошо формализованы и потому успешно реализованы в различных машинных программах статистического анализа. Метод исключения предполагает построение уравнения, включающего всю совокупность переменных, с последующим последовательным (пошаговым) сокращением числа переменных в модели до тех пор, пока не выполнится некоторое наперед заданное условие. Суть метода включения – в последовательном включении переменных в модель до тех пор, пока регрессионная модель не будет отвечать заранее установленному критерию качества. Последовательность включения определяется с помощью частных коэффициентов корреляции: переменные, имеющие относительно исследуемого показателя большее значение частного коэффициента корреляции, первыми включаются в регрессионное уравнение. Выше отмечено, что одной из предпосылок применения методов регрессионного анализа для построения эконометрических моделей является отсутствие среди независимых переменных (факторов) линейно связанных. Если данная предпосылка не выполняется, то возникает, как уже сказано выше, явление мультиколлинеарности, т.е. наличие сильной корреляции между независимыми переменными (включенными в модель факторами). В математическом аспекте мультиколлинеарность приводит к слабой обусловленности матрицы системы нормальных уравнений, т.е. близости ее определителя к нулю, а в содержательном аспекте - к искажению смысла коэффициентов регрессии и затруднению выявления наиболее существенно влияющих факторов. Основные причины, вызывающие мультиколлинеарность, – независимые переменные, либо характеризующие одно и то же свойство изучаемого явления, либо являющиеся составными частями одного и того же признака. В настоящее время существует ряд методов, позволяющих оценить наличие мультиколлинеарности в совокупности независимых переменных, измерить ее степень, выявить взаимно коррелированные переменные и устранить или ослабить ее негативное влияние на регрессионную модель. Наиболее распространенным методом выявления мультиколлинеарности является метод корреляции. На практике считают, что две переменные коллинеарны (линейно зависимы), если парный коэффициент корреляции между ними по абсолютной величине превышает 0,8. Устраняют мультиколлинеарность чаще всего путем исключения из модели одного из коррелированных факторов. Прогнозирование на основе регрессионных моделейВ процессе моделирования и прогнозирования социально-экономических процессов используется свойство тенденциозности социально-экономических систем и стремление к сохранению своего состояния в краткосрочный период. Следует отметить, что прогнозирование наиболее эффективно тогда, когда:
Использование регрессионных моделей в моделировании социально-экономических объектов и процессов осуществляется по многим направлениям в зависимости от вида применяемых функций. Например, парная линейная регрессия используется при принятии решений об оптимальном объеме потребления – 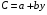 , где С – потребление; у – доход, а и b – параметры функции. , где С – потребление; у – доход, а и b – параметры функции.Если между экономическими явлениями существуют нелинейные соотношения, то они выражаются с помощью соответствующих нелинейных функций: например, равносторонней гиперболы, параболы второй степени и др. Например, равносторонняя гипербола  применяется для характеристики связи удельных расходов сырья, материалов, топлива с объемом выпускаемой продукции, времени обращения товаров от величины товарооборота как на микроуровне, так и на макроуровне. Классическим примером этой нелинейной функции является кривая Филипса, характеризующая нелинейное соотношение между нормой безработицы x и процентом прироста заработной платы y. применяется для характеристики связи удельных расходов сырья, материалов, топлива с объемом выпускаемой продукции, времени обращения товаров от величины товарооборота как на микроуровне, так и на макроуровне. Классическим примером этой нелинейной функции является кривая Филипса, характеризующая нелинейное соотношение между нормой безработицы x и процентом прироста заработной платы y.В 30-е годы XX в Дж М. Кейнс сформулировал гипотезу потребительской функции. С того времени исследователи неоднократно обращались к проблеме ее совершенствования Современная потребительская функция рассматривается как модель вида 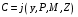 , y – доход, Р – цена, индекс стоимости жизни, М – наличные деньги, Z – ликвидные активы. , y – доход, Р – цена, индекс стоимости жизни, М – наличные деньги, Z – ликвидные активы.Особое место среди регрессий занимает группа производственных функций. Производственными функциями (ПФ) называют соотношения между используемыми в производстве материальными и трудовыми ресурсами и выпускаемой продукцией. По своему содержанию производственные функции охватывают всевозможные зависимости в сфере производства на различных уровнях – организация, объединение, комплекс, отрасль, региональная, национальная экономика. Интерпретация моделей регрессии осуществляется методами той отрасли знаний, к которой относится исследуемое явление. Но всякая интерпретация начинается со стати стической оценки уравнения регрессии в целом и оценки значимости входящих в модель факторных признаков. Для практического использования моделей регрессии большое значение имеет их адекватность, т.е. соответствие фактическим статистическим данным. Анализ качестваэмпирического уравнения парной и множественной линейной регрессииначинаютс построения эмпирического уравнения регрессии, которое является начальным этапом эконометрического анализа. Первое же, построенное по выборке уравнение регрессии, очень редко является удовлетворительным по тем или иным характеристикам. Поэтому следующей важнейшей оценкой является проверка качества уравнения регрессии. В эконометрике принята устоявшаяся схема такой проверки, которая проводится по следующим направлениям:
Для проверки общего качества уравнения как множественной регрессии, так и в случае парной регрессии, используется коэффициент детерминации 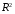 : : . (2.1) . (2.1)Справедливо соотношение  . Чем ближе этот коэффициент к единице, тем больше уравнение регрессии объясняет поведение . Чем ближе этот коэффициент к единице, тем больше уравнение регрессии объясняет поведение . .Для множественной регрессии коэффициент детерминации является неубывающей функцией числа объясняющих переменных. Добавление новой объясняющей переменной никогда не уменьшает значение 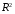 , так как каждая последующая переменная может лишь дополнить, но никак не сократить информацию, объясняющую поведение зависимой переменной. , так как каждая последующая переменная может лишь дополнить, но никак не сократить информацию, объясняющую поведение зависимой переменной.Иногда при расчете коэффициента детерминации для получения несмещенных оценок в числителе и знаменателе вычитаемой из единицы дроби делается поправка на число степеней свободы, т.е. вводится так называемый скорректированный (исправленный) коэффициент детерминации:  . (2.2) . (2.2)Соотношение (2.2) может быть представлено в следующем виде: 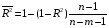 . (2.3) . (2.3)Из (2.3) очевидно, что 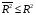 для для 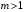 . С ростом значения m скорректированный коэффициент детерминации растет медленнее, чем обычный. Очевидно, что . С ростом значения m скорректированный коэффициент детерминации растет медленнее, чем обычный. Очевидно, что  только при только при 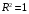 . . 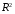 может принимать отрицательные значения. может принимать отрицательные значения.Доказано, что  увеличивается при добавлении новой объясняющей переменной тогда и только тогда, когда t-статистика для этой переменной по модулю больше единицы. Поэтому добавление в модель новых объясняющих переменных осуществляется до тех пор, пока растет скорректированный коэффициент детерминации. увеличивается при добавлении новой объясняющей переменной тогда и только тогда, когда t-статистика для этой переменной по модулю больше единицы. Поэтому добавление в модель новых объясняющих переменных осуществляется до тех пор, пока растет скорректированный коэффициент детерминации.Рекомендуется после проверки общего качества уравнения регрессии провести анализ его статистической значимости. Для этого используется F-статистика: 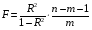 . (2.4) . (2.4)Из формулы (2.4) очевидно, что показатели F и 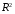 равны или не равны нулю одновременно. Если равны или не равны нулю одновременно. Если  , то , то  , следовательно, величина Y линейно не зависит от , следовательно, величина Y линейно не зависит от 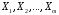 . .Расчетное значение F сравнивается с критическим Fкр. Fкр, исходя из требуемого уровня значимости α и чисел степеней свободы  и и 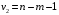 , определяется на основе распределения Фишера. Если , определяется на основе распределения Фишера. Если 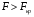 , то , то 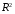 статистически значим. статистически значим.Статистическая значимость коэффициентов линейной регрессии проверяется на основе t-статистики: 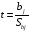 , (2.5) , (2.5)имеющей в данном случае распределение Стьюдента с числом степеней свободы 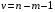 . При требуемом уровне значимости наблюдаемое значение t-статистики сравнивается с критической точкой . При требуемом уровне значимости наблюдаемое значение t-статистики сравнивается с критической точкой 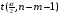 распределения Стьюдента. распределения Стьюдента.В случае, если 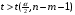 , то статистическая значимость соответствующего коэффициента регрессии подтверждается. Это означает, что фактор Xjлинейно связан с зависимой переменной Y. Если же установлен факт незначимости коэффициента bj, то рекомендуется исключить из уравнения переменную Xj. Это не приведет к существенной потере качества модели, но сделает ее более конкретной. , то статистическая значимость соответствующего коэффициента регрессии подтверждается. Это означает, что фактор Xjлинейно связан с зависимой переменной Y. Если же установлен факт незначимости коэффициента bj, то рекомендуется исключить из уравнения переменную Xj. Это не приведет к существенной потере качества модели, но сделает ее более конкретной.При оценке значимости коэффициентов линейной регрессии на начальном этапе также можно использовать «грубое» правило, позволяющее не прибегать к таблицам. Наиболее часто исследователя интересуют сами коэффициенты регрессии, поскольку они необходимы для построения прогноза, а также качественный анализ коэффициентов позволит судить о характере связи между данными. Поэтому, прежде всего, необходимо рассмотреть коэффициенты регрессии. Чем больше ве личина коэффициента регрессии, тем значительнее влияние данного признака на модели руемый. Знаки коэффициентов регрессии говорят о характере влияния на результативный признак. Если факторный признак имеет знак плюс, то с увеличением данного фактора результативный признак возрастает; если факторный признак имеет знак минус, то с его увеличением результативный признак уменьшается. Если экономическая теория подсказывает, что факторный признак должен иметь положительное значение, а он имеет знак минус, то необходимо проверить расчеты пара метров уравнения регрессии. Такое явление чаще всего бывает в силу допущенных оши бок при решении. Однако следует иметь ввиду, что когда рассматривается совокупное влияние факторов, то в силу наличия взаимосвязей между ними характер их влияния мо жет меняться. В эконометрических моделях на значения параметров уравне ния множественной регрессии могут накладываться ограни чения, связанные с величиной этих параметров, взаимосвязи их друг с другом. Примеры таких ограничений (2.6): 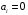 , , , (2.6) , (2.6) . .При наличии ограничений на параметры уравнения рег рессии возникает вопрос. Если ограничения справедливы, то каким образом обеспечить их выполнение в формируемой модели? Задачу определения уравнения регрессии с ограничениями на параметры часто называют задачей квадратичного программирования, поскольку ее решение сводится к минимизации квадратичной функции с ограничениями. Регрессия с ограничениями на коэффициентыПомимо рассмотренных классических уравнений регрессии, где для определения коэффициентов регрессии ставится лишь одно условие: средний квадрат ошибки значений отклика минимальным, может быть построено множество других уравнений. Часто относительно параметров регрессии имеется разнообразная априорная информация, которую можно представить в виде системы ограничений как линейных, так и нелинейных, налагаемых на коэффициенты p. Регрессия с простейшим видом линейных ограничений на коэффициенты: fk (p1, p2,..., pn) = 0, (3.1) pj ≥ 0, (3.2) где j = 1, 2,..., n – число коэффициентов, k – число ограничений. Рассмотрим регрессию с ограничениями на параметры на следующем примере. Чтобы приспособить свои учебные программы к потребностям практики, экономический факультет университета решил определить долю своих студентов, работающих в различных отраслях народного хозяйства. В результате опроса студентов прошлых выпусков получены следующие данные:  – количество выпускников в году – количество выпускников в году 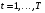 ; ; – количество выпускников года t, работающих в отрасли i, – количество выпускников года t, работающих в отрасли i,  , , 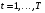 . .Чтобы по полученным данным предсказать долю λiбудущих выпускников, которые будут работать в отрасли  , можно воспользоваться методом наименьших квадратов и решить следующую задачу КП: , можно воспользоваться методом наименьших квадратов и решить следующую задачу КП: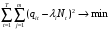 , , , (3.3) , (3.3) , ,  . .Таблица 1 – Данные о трудоустройстве выпускников 2001–2015 по результатам опроса
В табл. 1 отражены данные о количестве выпускников экономического факультета в период с 2001–2015 гг., работающих в следующих отраслях народного хозяйства: банковский сектор (q1), промышленность (q2), сфера услуг (q3), транспортные услуги (q4), государственные учреждения (q5), сельское хозяйство (q6) и торговля (q7). Таблица 2 – Доля выпускников работающих в отрасли i
Так, по всему ряду данных (таблица 1) с помощью МНК были найдены оценки коэффициентов регрессионной модели. Вычисления были выполнены с применением пакета прикладных программ обработки электронных таблиц MS Excel в среде Windows, результаты представлены в табл. 2. Значения коэффициентов позволяют судить о распределении выпускников экономического факультета по отраслям народного хозяйства. Если известно количество выпускников в последующих периодах, то можно получить приближенную оценку количества будущих выпускников, которые будут работать в той или иной отрасли. Этот метод позволяет достаточно просто в форме системы ограничений на коэффициенты учитывать разнообразную априорную информацию о моделируемом объекте, включая значимость влияющих факторов, возможные связи между ними и многое другое. Классический регрессионный анализ вряд ли следует использовать для решения рассмотренной задачи. заключениеКорреляционный и регрессионный анализ позволяют изучать статистические связи между переменными. Корреляционный анализ позволяет оценить влияние заданного фактора на изучаемый процесс, а методами регрессионного анализа можно выбрать конкретную математическую модель и оценить ее адекватность. Практическое значение регрессионной модели заключается в ее применение в моделировании и прогнозировании социально-экономических процессов. Поэтому при использовании моделей регрессии на практике большое значение имеет их адекватность, т.е. соответствие фактическим статистическим данным. Анализ коэффициентов регрессии позволяет установить степень значимости отдельных факторов для повышения уровня результативного показателя. Поэтому, очень часто исследователей интересует сами коэффициенты регрессии. Особое значение при этом имеет знак перед коэффициентом регрессии. Знаки коэффициентов регрессии говорят о характере влияния факторов на результативный признак. Их интерпретация полностью определяется социально-экономическим содержанием моделируемого признака. Если знаки коэффициентов не соответствуют характеру влияния факторного признака, свидетельствует о том, что в силу наличия взаимосвязи с другими факторами их поведение меняется. Либо классическая регрессионная модель не подходит для исследования данного объекта. Поэтому используют различные модификации регрессии. Одной из модификаций является регрессия с ограничениями на коэффициенты. Она позволяет найти значение целевой функции, при этом учитывая разнообразную априорную информацию о параметрах регрессии в виде системы ограничений. |
