Билет 1 икм

• Название: Билет 1 икм
• Дата: 14.01.2023
• Размер: 225.22 Kb.
• Имя файла: Otvety_na_bilety_bez_zadach.docx
• Тип: Документы; #886173
• страница: 4 из 5

2. Энтропия

Количество информации, которое заключено в некотором сообщении с вероятностью появления p(i), равно: I=-log₂p(i).Свойства количества информации:

1)чем меньше р, тем больше I.

2)количество информации в достоверном событии с вероятностью появления p=1 равно 0.

3)аддитивное свойство: количество информации, заключенное в совокупности двух независимых сообщений, равно сумме количеств информации, заключенных в каждом сообщении в отдельности.

4)количество информации величина неотрицательная.

Т.к. сообщения принимают различные значения с разными вероятностями, то ввели понятие энтропии (это среднее количество информации приходящееся на одно сообщение):

H=-∑^m_k=1 p_klogp_k, m – основание кода, p_k - вероятность определенного символа).

Энтропия дискретного источника независимых сообщений максимальна, если все сообщения равновероятны: Hmax=logm.

Избыточность это степень отличия энтропии от максимального значения: R=(Hmax-H)/Hmax.

Энтропия двоичного источника вычисляется по формуле:

H(m=2)=-p(1)*logp(1)-[1-p(1)]log[1-p(1)]

Энтропия двоичного источника максимальна если p(1)=p(0)=0.5

Чем больше энтропия, тем больше информации несет один символ и тем больше скорость передачи информации при заданной бодовой скорости - количество посылок в единицу времени

Основные способы увеличения энтропии:

1)наличие корреляционных связей между символами уменьшает энтропию.

Чтобы увеличить энтропию, мы кодируем не буквы а слова. Это называется укрупнение алфавита источника.

Эта же цель достигается путем предсказания - кодирования с предсказанием последующих символов по предыдущим

2) Неравновероятность символов уменьшает энтропию. Для устранения неравновероятности строят "кодовое дерево". Наиболее вероятные символы передаются наиболее короткими кодовыми комбинациями.

3)Для дальнейшего увеличения энтропии увеличивают основание кода m.


Билет 19

1. ФРК

При ФРК идеально разделены только два канала информации первого канала передается на несущей частоте U1(t)=Umsinw₀t, а второй передается на несущей частоте U2(t)=Umсosw₀t

Разделение каналов осуществляется за счет ортогональных несущих.

При ФРК оба канала передаются одинаково в одной и той же полосе, но разделяются.

Пусто по 1 каналу передается информация U1(t)=Umsinw₀t, а по 2 каналу U2(t)=Umсosw₀t

Прием осуществляется с помощи синхродетектора у которого два входа. На синхронный детектор поступает сумма U1(t)+U2(t), а на второй вход опорное напряжение Uопр(t)=Umsinw₀t , на второй детектор СД2 поступает на первый вход таже суммаU1(t)+U2(t), а на второй вход опорное напряжение Uопр(t)=Umcosw₀t

Напряжение на выходе синхронного детектора равно:

U_выхСД1=∫[ U1(t)+U2(t)] Uопр1(t)dt=1/T∫ U1(t) sinw₀t sinw₀t dt+1/T∫U2(t) cosw₀t sinw₀t dt= 1/T∫(U1(t)Um)/2=(U1(t) за время t практический не миняется)= U1(t)Um)/2 это информация 1-го канала.

Причины взаимных помех: разность фаз несущих частот на передача не равно 90⁰; фазы опорных напряжений не равны точно фазам несущих частот первого и второго каналов; операция интегрирования реализуется с погрешностями. Способы уменьшения взаимных помех: усовершенствовать систему частотной и фазовой синхронизации; следует уменьшить погрешности реализации операции интегрирования.

2. Циклический код (7,4)

Код называется циклическим, если циклическая перестановка одной кодовой комбинации дает все остальные кодовые комбинации данного кода.

10110

01011

10101

11010

Код называется циклическим, если циклическая перестановка одной кодовой комбинации дает все остальные кодовые комбинации данного кода. Каждая комбинация такого кода записывается в виде полинома. Состоит из 7 символов, из которых 4 информационных и 3 проверочных.

Алгоритм формирования: записываются возможные информационные комбинации; каждую комбинацию записывают в виде полинома (а3,а2,а1,а0); выбираем образующий полином, степень которого соответствует количеству проверочных символов ; полином, соответствующий информационной комбинации, умножается на образующий полином.

Алгоритм декодирования: принятая кодовая комбинация делится на образующий полином, остаток от деления есть синдром, который указывает, где произошла ошибка; формируем вектор ошибки (т.е. кодовую комбинацию с ошибкой) на основании синдрома.

Кодовое расстояние – количество позиций, в которых одна кодовая комбинация отличается от другой. Здесь минимальное кодовое расстояние равно 3 (т.е. код исправляет все одиночные ошибки).

Теория циклических кодов базируется на теории двоичных полиномов(полиномиальные коды)

Каждая комбинация такого кода записывается в виде полинома


Билет 20

1. Характеристики ЦФ

ЦФ – это микроЭВМ, которая решает задачу фильтрации средствами вычислительной техники. Описывается разностным уравнением, которое является цифровым эквивалентом аналогового дифференциального уравнения: y_i==∑^L_l=1 a_ly_i-l+=∑^M_m=0 b_mx_i-m. Максимум из L,M определяет порядок фильтра.

Характеристики:

Импульсная реакция ЦФ (g) – реакция фильтра на единичный импульс (из разностного уравнения, где для y:реакция не опережает воздействие; для х: 1при i=0, 0 при i≠0).

Переходная характеристика ЦФ (h) – реакция фильтра на дискретную функцию единичного скачка (из разностного уравнения, где для для y:реакция не опережает воздействие; для х: 1при i≥0, 0 при i<0; из импульсной характеристики: h=∑ⁱ_k=0 g_k).

Передаточная характеристика ЦФ (K(z)) – отношение z-преобразования выходного процесса y(z) к z-преобразованию входного процесса x(z). Из нее можно получить выражения для АЧХ и ФЧХ фильтра, а также определить является ли фильтр устойчивым (корни числителя – нули, корни знаменателя – полюсы; ЦФ устойчив если полюсы лежат внутри окружности единичного радиуса).
2. Оптимальный корреляционный приемник

Оптимальный корреляционный приемник - это приемник для двоичных сигналов с одинаковой энергией

Приемник реализующий потенциальную помехоустойчивость, т.е. обеспечивающий минимальную вероятность ошибки, называется оптимальным приемником

Эта минимальная вероятность ошибки может быть большой, но никакой другой приемник не даст меньшей вероятности ошибки.

Правило работы оптимального приемника может быть только статистическим.

∫U₁²(t)dt=∫U₀²(t)dt (c одинаковыми энергиями)

Алгоритм работы:

∫[z²(t)-2z(t)U₁(t)+ U₁²(t)]dt <∫[z²(t)-z(t)U₀(t)+ U₀²(t)]dt то R=1;

И тогда

∫z(t)U₁(t)dt > ∫z(t)U₀(t)dt то R=1

∫z(t)U₁(t)dt < ∫z(t)U₀(t)dt то R=0
Структурная схема:


Генер U1(t)


1




Перемн

Интегр.



РУ

Z(t)










Перемн

Интегр.

2










Генер U0(t)

Билет 21

1. СФ

Оптимальный фильтр – это фильтр, обеспечивающий на выходе максимальное отношение мощности сигнала к мощности шума. Если помеха, поражающая сигнал, является белым шумом, то оптимальный фильтр называется согласованным фильтром.

Фильтр называется согласованным т.к.:

1)обеспечивает максимальное отношение с/ш на выходе: h0²=Ec/G0

2)характеристики СФ согласованы с характеристиками сигнала

а)импульсная реакция СФ совпадает с зеркальным отображением согласованного с ним сигнала

б) АЧХ СФ совпадает с амплитудным спектром сигнала(с точностью до постоянного множителя)

в)ФЧХ СФ противоположна по знаку ФЧХ сигнала

Докажем основные свойства согласованного фильтра:

Uвых(t)=∫z(τ)g(t-τ)d τ= ∫Uc(τ)g(t- τ)dτ +∫x(τ)g(t- τ)dτ – напряжение на выходе фильтра.

Напряжение полезного сигнала ∫Uc(τ)g(t- τ)dτ.

Мощность полезного сигнала [∫Uc(τ)gcф(t- τ)dτ]² (на единичном сопротивлении).

Мощность помехи (дисперсия)

[∫x(τ)g(t- τ)dτ]²=∫x(τ)g(t- τ)dτ*∫x(V)g(t- V)dV=G₀∫б(τ-V)g(t-τ)dτ∫ g(t-V)dV=G0∫ g²(t-V)dV

Где В(τ-v)= x(τ)x(V)=G₀ δ (τ-V)

Используем фильтрующие свойства δ-функции

∫ δ (τ-V)y(t)dt=y(τ) то есть ∫ δ (τ-V)g(t-τ)dτ= g(t-V)

Отношение сигнал и шум:

Pc/σ²=[∫Uc(τ)g(t- τ)dτ]²/ G₀∫ g²(t-V)dV≤ ∫U²c(τ)g²(t- τ)dτ / G₀∫ g²(t-V)dV≤ ∫ U²c(τ)dτ/ G₀

Поскольку подынтегральное выражение не отрицательно, то интеграл будет максимален. Согласованный фильтр дает на выходе в момент времени t=T максимальное отношение сигнал шум, равный h0=∫ U²c(τ)dτ/ G₀=Ec/G0 где Ес- энергия сигнала.

2. Теорема Шеннона

По каналу связи с полосой пропускания F, в котором действует сигнал с мощностью Pc и нормальный шум с дисперсией σ² можно передавать информацию со скоростью сколько угодно близкой к пропускной способности канала С=Flog(1+Pc/ σ²) и при этом вероятность ошибки может быть сделана сколь угодно малой.

Производительность источника – это количесвто информации, производимой источником в единицу времени: H’=H/T (H - энтропия, T – длительность сообщения).

Скорость передачи информации – количество взаиной информации передаваемой по каналу связи в единицу времени: I’=lim(I(Z,U)/T).

Пропускная способность канала вязи – максимально возможная скорость передачи информации.

Доказательство:

Количество взаимной информации содержащейся в процессе z(t) о сигнала u(t):

I(Z,U)=h(z)-h(X) (h(z), h(X) – дифференциальные энтропии соответствующих процессов).

Дифференциальная энтропия – относительная информационная содержательность непрерывного процесса (h(z)=-∫W(z)log(Wz)dz). Т.к. шум нормальный и его дисперсия σ²=G0F, то: h(X)=0.5log(2πe σ²). Чтобы энтропия процесса z была максимальной, этот процесс должен быть нормальным случайным процессом с дисперсией Рс. Тогда максимальное количество взаимной информации равно: I(Z,U)= 0.5log(2πe (σ²+Рс))- 0.5log(2πe σ²)= 0.5log(2πe(1+Рс/σ²). Т.к. процесс на выходе канала связи финитный по спектру, то полностью определяется по теореме Котельникова, т.о. в единицу времени следует передавать 2F отсчетов, тогда получаем: C=2F*I(Z,U).

Билет 22

1. ШПС

К некоторым системам связи предъявляется требование скрытности. Противник не должен обнаружить факт передачи. Сигнал нужно спрятать в шумах, чтобы обычный сигнал принять с хорошим качеством, он должен быть мощнее шумов, резко выделяться.

ШПС(шумоподобный сигнал) - сигналы с широким спектром, т.е. мощность передатчика распределяется по большой полосе частот и спектральная плотность такого сигнала мала. Сигнал малозаметен на фоне помех.

К таким сигналам относятся:

-Коды Баркера (3,5,7,11,13)

-М - последовательности (длина сотни импульсов)

Их называют псевдослучайные последовательности(ПСП). Их база B=2FT (гдеF-ширина спектра ППС;T-длительность ПСП)

Согласованные фильтры обычно используются для оптимального приема шумоподобных сигналов, аналоговый фильтр согласованный с ШПС содержит: линию задержки, фазовращатели (если + знак не меняется, если – знак меняется на противоположный), сумматор, фильтр согласованный с одиночным прямоугольным импульсом.

2. Энтропия

Количество информации, которое заключено в некотором сообщении с вероятностью появления p(i), равно: I=-log₂p(i).Свойства количества информации:

1)чем меньше р, тем больше I.

2)количество информации в достоверном событии с вероятностью появления p=1 равно 0.

3)аддитивное свойство: количество информации, заключенное в совокупности двух независимых сообщений, равно сумме количеств информации, заключенных в каждом сообщении в отдельности.

4)количество информации величина неотрицательная.

Энтропия H - это среднее кол-во информации приходящееся на одно сообщение

Для дискретного источника независимых сообщений энтропия вычисляется по формуле:

H=-∑^m_k=1 p_klogp_k, m – основание кода, p_k - вероятность определенного символа).

Энтропия дискретного источника независимых сообщений максимальна, если все сообщения равновероятны Hmax=logm

Избыточность это степень отличия энтропии от максимального значения: R=(Hmax-H)/Hmax

Наиболее часто используются двоичные системы связи m=2. Энтропия двоичного источника вычисляется по формуле:

H(m=2)=-p(1)*logp(1)-[1-p(1)]log[1-p(1)]

Энтропия двоичного источника максимальна если p(1)=p(0)=0.5

Чем больше энтропия, тем больше информации несет один символ и тем больше скорость передачи информации при заданной бодовой скорости - количество посылок в единицу времени

Основные способы увеличения энтропии:

1)наличие корреляционных связей между символами уменьшает энтропию.

Чтобы увеличить энтропию, мы кодируем не буквы а слова. Это называется укрупнение алфавита источника.

Эта же цель достигается путем предсказания - кодирования с предсказанием последующих символов по предыдущим

2) Неравновероятность символов уменьшает энтропию. Для устранения неравновероятности строят "кодовое дерево"

Наиболее вероятные символы передаются наиболее короткими кодовыми комбинациями.

3)Для дальнейшего увеличения энтропии увеличивают основание кода m.

Билет 23

1. Оптимальный приемник двоичных сигналов

Способность Системы связи препятствовать мешающему влиянию помех называется помехоустойчивостью. Максимально достижимая помехоустойчивость называется потенциальная помехоустойчивость, которой соответствует минимальная вероятность ошибки р (р=limNoш/N (где N –общее количество переданных символов, Nош- количество ошибок).

Система связи работает с такими вероятностями: р=10^-1−10^-3 удовл.качество

р=10^-4−10^-6 хорошее качество (используют для передачи речи); р=10^-7−10^-9 отличное.

Приемник реализующий потенциальную помехоустойчивость, т.е. обеспечивающий минимальную вероятность ошибки, называется оптимальным приемником

Правило работы оптимального приемника, если передаваемый сигнал двоичный:

если р(1/z)>p(0/z) решение R=1

если р(1/z)
Пусть в линии связи действует единственная помеха (АБГШ), со спектральной плотность G₀, тогда сравнение условной вероятностей эквивалентно следующему сравнению:

∫[z(t)-U₁(t)]²dt <∫[z(t)-U₀(t)]²dt R=1; ∫[z(t)-U₁(t)]²dt >∫[z(t)-U₀(t)]²dt R=0

Структурная схема идеального приемника Катальникова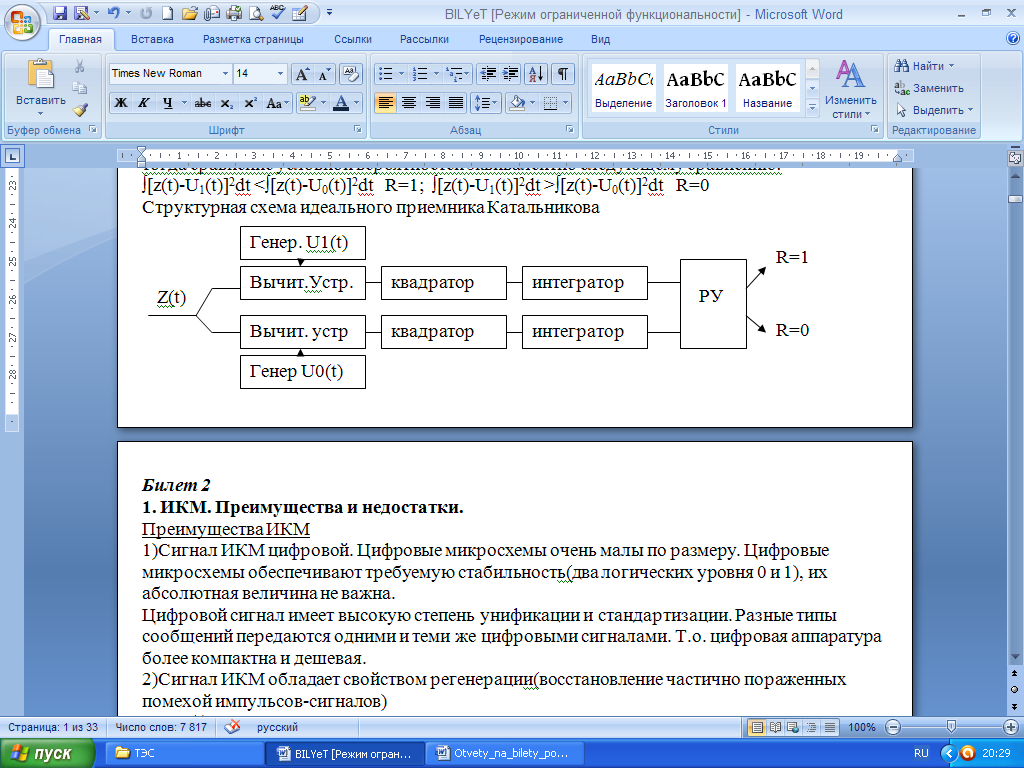


Физическая сущность "0" и "1" зависит от вида модуляции.

1)Двоичная амплитудная модуляция(ДАМ)

U1(t)=UmCosw0t

U0(t)=0

2)Двоичная частотная модуляция(ДЧМ)

U1(t)=UmCosw1t

U0(t)=UmCosw0t

3)Двоичная фазовая модуляция(ДФМ)

U1(t)=UmSinw0t

U0(t)=-UmSinw0t

2. Преимущества и недостатки ИКМ

Преимущества ИКМ

1)Сигнал ИКМ цифровой. Цифровые микросхемы очень малы по размеру. Цифровые микросхемы обеспечивают требуемую стабильность(два логических уровня 0 и 1), их абсолютная величина не важна.

Цифровой сигнал имеет высокую степень унификации и стандартизации. Разные типы сообщений передаются одними и теми же цифровыми сигналами. Т.о. цифровая аппаратура более компактна и дешевая.

2)Сигнал ИКМ обладает свойством регенерации(восстановление частично пораженных помехой импульсов-сигналов)

если z(t)>V то на выходе 1

если z(t)
Без регенерации происходит накопление шумов при переприеме.

При регенерации складываются не шумы, а ошибки. Это позволяет на порядок увеличить дальность связи.

Недостатки ИКМ

1)Ширина спектра сигнала ИКМ значительно больше ширины спектра исходного аналогового сигнала. Ширина спектра сигнала ИКМ равна ширине спектра одиночного импульса.

Ширина спектра ИКМ в 2n раз больше ширины спектра исходного аналогового сигнала.(n-длина кодовой комбинации) (Т=1/2nFв – длительность одного импульса, Пикм=1/Т).

2)Операция квантования приводит к тому, что сигнал ИКМ поражается специфической помехой, которая называется "шум квантования". При квантовании истинный уровень заменяется ближайшим разрешенным.

Квантование эквивалентно наложению на сигнал ИКМ помехи («шум квантования», его мощность: σ²=Δ²/12=(Umax)²/(N-1), N – число уровней квантования, Δ - шаг).

Для уменьшения квантования нужно увеличивать число уровней квантования, но при этом увеличивается длина кодовой комбинации и расширяется спектр ИКМ, чтобы этого избежать используется неравномерное квантование (маленькие уровни квантуются с маленьким шагом квантования, а большие уровни с большим).

Билет 24