Билет 1 икм

• Название: Билет 1 икм
• Дата: 14.01.2023
• Размер: 225.22 Kb.
• Имя файла: Otvety_na_bilety_bez_zadach.docx
• Тип: Документы; #886173
• страница: 2 из 5

Оптимальный приемник двоичных сигналов.

Способность Системы связи препятствовать мешающему влиянию помех называется помехоустойчивостью. Максимально достижимая помехоустойчивость называется потенциальная помехоустойчивость, которой соответствует минимальная вероятность ошибки р (р=limNoш/N (где N –общее количество переданных символов, Nош- количество ошибок).

Приемник реализующий потенциальную помехоустойчивость, т.е. обеспечивающий минимальную вероятность ошибки, называется оптимальным приемником

Эта минимальная вероятность ошибки может быть большой, но никакой другой приемник не даст меньшей вероятности ошибки.

р(1/z)-условная вероятность информации передачи 1 если на входе приемника процесс z(t)

р(0/z)-условная вероятность информации передачи 0 если на входе приемника процесс z(t)

Правило работы оптимального приемника может быть только статистическим.

если р(1/z)>p(0/z) решение R=1

если р(1/z)
Пусть в линии связи действует единственная помеха (АБГШ), со спектральной плотность G₀, тогда сравнение условной вероятностей эквивалентно следующему сравнению:

∫[z(t)-U₁(t)]²dt <∫[z(t)-U₀(t)]²dt R=1; ∫[z(t)-U₁(t)]²dt >∫[z(t)-U₀(t)]²dt R=0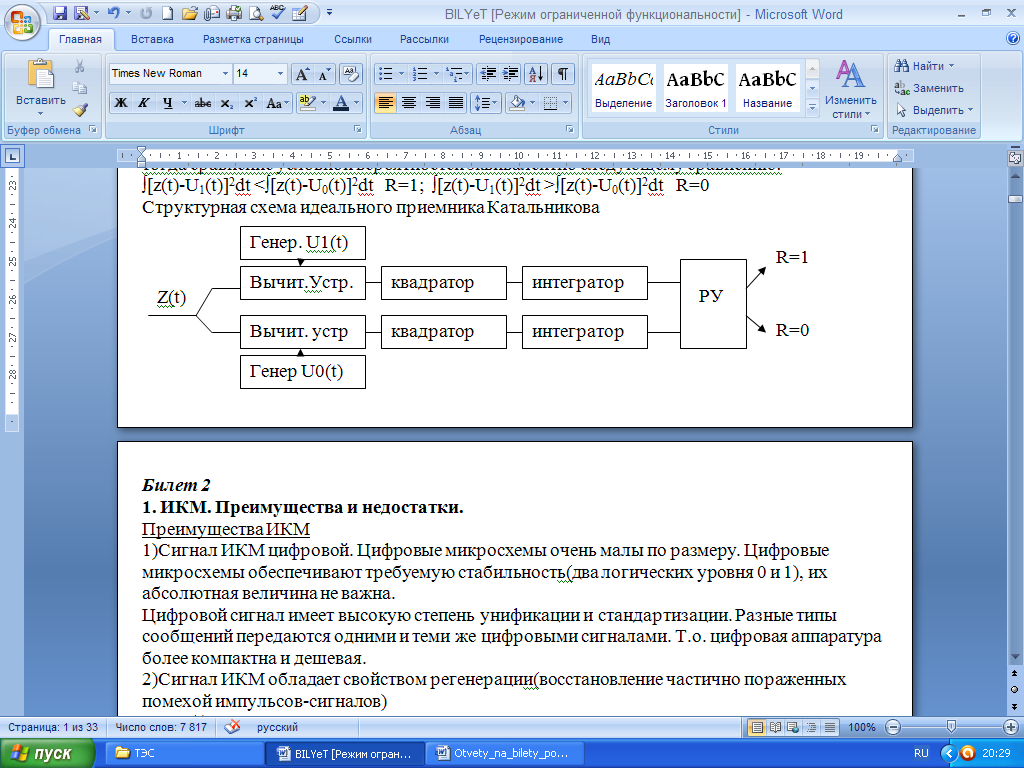


Физическая сущность "0" и "1" зависит от вида модуляции.

1)Двоичная амплитудная модуляция(ДАМ)

U1(t)=UmCosw0t

U0(t)=0

2)Двоичная частотная модуляция(ДЧМ)

U1(t)=UmCosw1t

U0(t)=UmCosw0t

3)Двоичная фазовая модуляция(ДФМ)

U1(t)=UmSinw0t

U0(t)=-UmSinw0t

2. Количество информации. Энтропия.

Количество информации, которое заключено в некотором сообщении А с вероятностью появления p(А), равно: I=-log₂p(А).Свойства количества информации:

1)чем меньше р, тем больше I (количество информации.)

2)количество информации в достоверном событии с вероятностью появления p=1 равно 0.

3)аддитивное свойство: количество информации, заключенное в совокупности двух независимых сообщений, равно сумме количеств информации, заключенных в каждом сообщении в отдельности.

4)количество информации величина неотрицательная.

Энтропия H - это среднее кол-во информации приходящееся на одно сообщение

Для дискретного источника независимых сообщений энтропия вычисляется по формуле:

Т.к. сообщения принимают различные значения с разными вероятностями, то ввели понятие энтропии (это среднее количество информации приходящееся на одно сообщение):

H=-∑^m_k=1 p_klogp_k, m – основание кода, p_k - вероятность определенного символа)

Энтропия дискретного источника независимых сообщений максимальна, если все сообщения равновероятны

Hmax=logm

Наиболее часто используются двоичные системы связи m=2. Энтропия двочного источника вычисляется по формуле:

H(m=2)=-p(1)*logp(1)-[1-p(1)]log[1-p(1)]

Энтропия двоичного источника максимальна если p(1)=p(0)=0.5

Основные способы увеличения энтропии:

1)наличие корреляционных связей между символами уменьшает энтропию.

Чтобы увеличить энтропию, мы кодируем не буквы а слова. Это называется укрупнение алфавита источника.Эта же цель достигается путем предсказания - кодирования с предсказанием последующих символов по предыдущим

2) Неравновероятность символов уменьшает энтропию. Для устранения неравновероятности строят "кодовое дерево". Наиболее вероятные символы передаются наиболее короткими кодовыми комбинациями.

3)Для дальнейшего увеличения энтропии увеличивают основание кода m

Билет 7

1. Потенциальная помехоустойчивость.

Способность системы связи препятствовать мешающему влиянию помех называется помехоустойчивостью.

Максимально достижимая помехоустойчивость называется потенциальной помехоустойчивостью.

Количественной мерой помехоустойчивости называется вероятность ошибки

P=lim(N->∞)Nош/N

N-общее количество переданных символов, сообщений

Nош-количество ошибок, т.е. количество неверно принятых символов, сообщений

Высокой помехоустойчивости соответствует малая вероятность ошибки, низкой помехоустойчивости соответствует большая вероятность ошибки.

Потенциальной помехоустойчивости соответствует минимальная вероятность ошибки.

Система связи работает с такими вероятностями: р=10^-1−10^-3 удовл.качество

р=10^-4−10^-6 хорошее качество (используют для передачи речи); р=10^-7−10^-9 отличное.

Приемник, реализующий потенциальную помехоустойчивость, т.е. обеспечивающий минимальную вероятность ошибки, называется оптимальным приемником.

Приемник реализующий потенциальную помехоустойчивость, т.е. обеспечивающий минимальную вероятность ошибки, называется оптимальным приемником

2. Укрупнение сообщений

Энтропия – это среднее количество информации приходящееся на одно сообщение. Чем больше энтропия, тем больше информации несет один символ и тем больше скорость передачи информации. Чем больше энтропия, тем больше информации несет один символ и тем больше скорость передачи информации при заданной бодовой скорости - количество посылок в единицу времени

Основные способы увеличения энтропии:

1)наличие корреляционных связей между символами уменьшает энтропию.

Чтобы увеличить энтропию, мы кодируем не буквы а слова. Это называется укрупнение алфавита источника.

Эта же цель достигается путем предсказания - кодирования с предсказанием последующих символов по предыдущим

2) Неравновероятность символов уменьшает энтропию. Для устранения неравновероятности строят "кодовое дерево"

Наиболее вероятные символы передаются наиболее короткими кодовыми комбинациями.

3)Для дальнейшего увеличения энтропии увеличивают основание кода m.

Укрупнения сообщений:

Цель статистического кодирования- увеличить энтропию и увеличить скорость передачи информации.

Пример: порядок расчета энтропии источника зависимых сообщений

1. 
   Определить общее количество N независимых слов источника. N=mⁿ (m=2;n=2)
   
2. 
   Определим вероятность каждого слова: p(AM)= p(A)*p(M/A); p(MA)=p(M)*p(A/M); p(AA)=p(A)*p(A/A); p(MM)=p(M)*p(M/M)
   
3. 
   Т.к. энтропия независимы то энтропия источника «на слово» найдем по формуле:
   

Нсл= −p(AM)logp(AM)-p(MA)logp(MA)-p(MM)logp(MM)-p(AA)logp(AA)= [дв.ед./слово]

4. 
   Энтропия на одну букву или символ(n=2): H=Hcл/n=0,828 [дв.ед/cимвол]; Избыточность т.е степень отличия энтропии источника от максимального значение R=(H_max-H)/H_max где H_max=log₂2=1
   
5. 
   Т.к. разных слов 4 то нужно использовать код с основание m=4, длина кодовой комбининации n=1, то общее число комбинаций N=4
   

Энтропия рассчитывает по формуле дискретного источника независимых сообщений:

Нсл= −p(1)logp(1)-p(2)logp(2)-p(3)logp(3)-p(4)logp(4)=1,659. [дв.ед./сообщение]

Таким образом увеличили энтропию в 2 раза. Определим избыточность источника, для H_max=log₂4=2; R=1-H/ H_max Избыточность осталось та же Т.о. увеличив энтропию мы не уменьшаем избыточность. Это означает, что есть возможность еще более увеличить энтропию.

Билет 8

1. Потенциальная помехоустойчивость ДАМ,ДЧМ,ДФМ.

Способность Системы связи препятствовать мешающему влиянию помех называется помехоустойчивостью. Максимально достижимая помехоустойчивость называется потенциальная помехоустойчивость, которой соответствует минимальная вероятность ошибки р (р=limNoш/N (где N –общее количество переданных символов, Nош- количество ошибок).

Приемник, реализующий потенциальную помехоустойчивость, т.е. обеспечивающий минимальную вероятность ошибки, называется оптимальным приемником. (Это минимальная вероятность ошибки не может быть очень большой, но ни какой другой приемник не даст меньшей вероятности ошибки).

Что бы обеспечить потенциальную помехоустойчивость оптимальный приемник должен работать по правилу: ∫[z(t)-U₁(t)]²dt <∫[z(t)-U₀(t)]²dt R=1;

∫[z(t)-U₁(t)]²dt >∫[z(t)-U₀(t)]²dt R=0

Полной характеристикой помехоустойчивости является средняя вероятность ошибки

p=p(1)*p(0/1)+p(0)*p(1/0)

m1=0

disp^2=G0*Ep

Выводы:

1)максимальная вероятность ошибки равна: Pmax=1-F(0)=0.5 для двоичной системы связи

2)чем больше Ер, тем меньше вероятность ошибки и при Ep->inf; p=>1-F(inf)=0

3)потенциальная помехоустойчивость ОП не зависит от формы посылок, зависит только от Ер

4)наиболее помехоустойчивым будет тот вид модуляции, который обеспечивает max Ep при фиксированной мощности передатчика

Epдам=Um^2 * T/2

Ердчм=Um^2 * T

Ердфм=2Um^2 * T

Т.о. наиболее помехоустойчивым способом передачи двоичных сигналов является ДФМ.Она выигрывает в 2 раза по мощности передатчика по сравнению с ДЧМ и в 4 раза по мощности передатчика по сравнению с ДАМ.

Чем меньше мощность, тем меньше передатчик, меньше потребляемая энергия источника питания, тем он дешевле.

PошДАМ=1-F(h0/2^1/2)

РошДЧМ=1-F(h0)

РошДФМ=1-F(h0*2^1/2)

2. Построение кодового дерева.

Энтропия – это среднее количество информации приходящееся на одно сообщение. Чем больше энтропия, тем больше информации несет один символ и тем больше скорость передачи информации

Префиксные свойства: не какая короткая кодовая комбинация не может быть началом более длиной кодовой комбинации.

Неравновероятность символов уменьшает энтропию. Для устранения неравновероятности строят "кодовое дерево"

Наиболее вероятные символы передаются наиболее короткими кодовыми комбинациями.

Алгоритм построения кодового дерева:

1)располагаем сообщения в порядке убывания вероятности

2)два сообщения с наименьшими вероятностями объединяем в одно, вероятность которого равна сумме вероятностей объединяемых сообщений, далее п1(цикл)

3)до тех пор пока не получим суммарную вероятность p=1
Билет 9

1. Некогерентный прием ДАМ. Распределения на выходе детектора.

Оптимальный прием требует точного знания опорных сигналов U0(t) и U1(t) с точностью до фазы. Такой приемник называется когерентным. Он сложный, дорогой, требует сложной настройки. На практике часто используются дешевые, простые, некогерентные способы приема.

Структурная схема НКГ приемника имеет вид: 1

->ПФ->Амплитудный детектор->пороговое устройство <

0

На входе ПФ действует сигнал + АБГШ

Процесс на выходе ПФ z(t)=x(t)+{u1(t); u0(t)}

Амплитудный детектор выделяет огибающую процесса z(t)

Для нормального шума огибающая распределена по закону Релея(если передаем U0(t)=0)

z(t)=x(t)

при передаче 1 z(t)=x(t)+UmCosw0t

Огибающая суммы нормального шума и гармонического колебания распределена по закону Райса

Оптимальное пороговое напряжение для равновероятных 1 и 0 p(1)=p(0) совпадает с точкой пересечения, при этом средняя вероятность ошибки минимальна. Суммарная площадь характеризует среднюю вероятность ошибки.

Оптимальное пороговое напряжение для равновероятных 1 и 0 p(1)=p(0) совпадает с точкой пересечения, при этом средняя вероятность ошибки минимальна. Суммарная площадь характеризует среднюю вероятность ошибки. Вероятность ошибки для некогерентного приема сигнала ДАМ определяется по формуле: p=0.5 exp(-h²/4)

2. Увеличение энтропии путем увеличения m

Символы кода К3 практически равновероятны. Каждый несёт одну двоичную единицу. Объединим символы кода К3 в пары и закодируем из новым кодом К4. Пары кода К3 называют дебиты.

Все символы практически равновероятны, следовательно каждый символ кода К4 имеет энтропию Hmax=log4=2

Символы нового двоичного кода К3(m=2), равновероятный и символ переносит 1дв.ед. информации. Комбинации из двух двоичных символов (бит) называют дибитами.

Билет 10

1. Некогерентный прием ДЧМ. Распределения на выходе детектора.

Оптимальный прием требует точного знания опорных сигналов U0(t) и U1(t) с точностью до фазы. Такой приемник называется когерентным. Он сложный, дорогой, требует сложной настройки. На практике часто используются дешевые, простые, некогерентные способы приема.

Структурная схема НКГ приемника имеет вид:

ПФ->Амплитудный детекторU1-> 1

-> ->Решающее устройство <

ПФ->Амплитудный детекторU0-> 0

U1- огибающая на выходе амплитудного детектора 1

W(u0/1) W(u1/1)

При передаче 1 на вход детекторов поступает процесс z(t)=UmCosw1t+x(t)

Через ПФ1 проходит сигнал+шум, поэтому распределение W(u1/1) - распределение Райса.

На выходе ПФ1 будет только шум и распределение W(u0/1) - Релеевское распределение

При передаче 0 на вход детекторов поступает процес z(t)=UmCosw0t+x(t)

На выходе ПФ1 только шум, W(u1/0) - Релеевское распределение

На выходе ПФ0 сигнал+шум, поэтому W(u0/0) - распределение Райса.

W(u1/0) W(u0/0)

Оптимальное пороговое напряжение для равновероятных 1 и 0 p(1)=p(0) совпадает с точкой пересечения, при этом средняя вероятность ошибки минимальна. Суммарная площадь характеризует среднюю вероятность ошибки. Вероятность ошибки для некогерентного приема сигнала ДЧМ определяется по формуле: p=0.5 exp(-h²/2)

2. Увеличение энтропии путем предсказания.

Энтропия – это среднее количество информации приходящееся на одно сообщение. Чем больше энтропия, тем больше информации несет один символ и тем больше скорость передачи информации.

Для устранения корреляционных связей между сообщениями источника мы рассматриваем способ укрупнения сообщения(кодировали не буквы а целые слова) При этом энтропия увеличивается, но помехоустойчивость уменьшается. При этом также резко усложняется кодек-кодер+декодер. Двоичный кодек помнит только два сообщения: 0 и 1(m=2) Если мы кодируем буквы, то нужно запомнить 33 буквы, если кодирумем слова, то нужно щапоминать тысячи-сотни тысяч разных символов, поэтому такой способ используется для небольшого количества слов.

Технически более просто устраняются корреляционные связи с помощью кодирования с предсказанием.

Кодирование с предсказанием позволяет уменьшить динамический диапазон передаваемого сигнала. Т.о. при ИКМ уменьшается необходимое количество уровней квантования при заданной дисперсии шума квантования(при заданном L уменьшается дисперсия шума квантования)


Билет 11

1. ДОФМ

Двоичная относительная фазовая модуляция

Для приема сигнала ДФМ необходимо иметь на приеме когерентное опорное напр.

->ФД перемножитель->Tint0

^

ГОН

cosw0t

Опорное напряжение может быть получено только из принимаемого сигнала, т.к. он меняется в тракте(линии связи)

ГОН содержит умножитель частоты на 2(снимает модуляцию), узкополосный фильтр(фильтрует сигнал от помех), делитель частоты на 2(триггер)

На выходе ГОН фаза сигнала случайно меняется на 180град.

На выходе интегратора 1 в 0, а 0 в 1. Такое явление называется "обратная работа"

Для борьбы с этим используется ДОФМ: информация заключена в разности фаз соседних посылок. При передаче 0 фаза n посылки фиn равна фазе предыдущей (n-1) посылки фи(n-1)

При передаче 1 фаза n посылки фиn отличается на 180град от фазы (n-1) посылки

Для упрощения схемы модулятора при ДОФМ на передачу включается блок внесения относительности(БВО) между кодером и модулятором.

Прием сигнала ДОФМ осуществляется двумя способами:

1)прием ДОФМ «сравнением полярностей»: сигнал будет принят правильно, если n и (n-1) посылки приняты верно, либо если обе приняты неверно. Вероятность ошибки равна:

Рош=2F(√2* h0)*(1-F(√2 * h0))

h0=0 Pош=0.5

2)Прием ДОФМ «сравнением фаз» (некогерентный способ прием): в фазовом детекторе сравниваются данная посылка и передающая. Вероятность ошибки для приема сравнением фаз равна: Pош=0.5*e^-h^2

Для НКГ способов передачи ДОФМ наиболее помехоустойчивый способ передачи.

Выигрывает в 4 раза по мощности передатчика по сравнению с ДАМ и в 2 раза по мощности передатчика по сравнению с ДЧМ.

2. Кодирование с предсказанием. ДИКМ

Для устранения корреляционных связей между сообщениями источника мы рассматриваем способ укрупнения сообщения(кодировали не буквы а целые слова) При этом энтропия увеличивается, но помехоустойчивость уменьшается. При этом также резко усложняется кодек-кодер+декодер. Двоичный кодек помнит только два сообщения: 0 и 1(m=2) Если мы кодируем буквы, то нужно запомнить 33 буквы, если кодируем слова, то нужно запоминать тысячи-сотни тысяч разных символов, поэтому такой способ используется для небольшого количества слов.Технически более просто устраняются корреляционные связи с помощью кодирования с предсказанием.

Коэффициенты предсказания Cjk подбираются таким образом, чтобы обеспечить минимальную среднеквадратическую погрешность предсказания xк, т.е. решается система линейных уравнений

Вычисленные погрешности предсказания(некоррелированные) кодируются и передаются в линию связи. Такая система связи называется дифференциальная ИКМ (ДИКМ)

Кодирование с предсказанием позволяет уменьшить динамический диапазон передаваемого сигнала. Т.о. при ИКМ уменьшается необходимое количество уровней квантования при заданной дисперсии шума квантования(при заданном L уменьшается дисперсия шума квантования)

Билет 12