Билет 15 Сеточные методы на примере решения уравнения теплопроводности

• Название: Билет 15 Сеточные методы на примере решения уравнения теплопроводности
• Анкор: №15.2.docx
• Дата: 14.07.2018
• Размер: 52.86 Kb.
• Имя файла: №15.2.docx
• Тип: Документы; #21466

Билет №15 Сеточные методы на примере решения уравнения теплопроводности

1. Введение

Эта работа знакомит с численными методами решения дифференциальных уравнений в частных производных параболического типа на примере одномерного линейного уравнения теплопроводности. Рассматривается следующая краевая задача:

                       

                          

                        

                       

2. Теоретическая справка

2.1. Дифференциальная краевая задача

Как уже было отмечено, в работе рассматривается задача:

                       

                          

                        

                       

2.2. Сеточная область

Для рассмотренной задачи

            p = 0, 1, ..., P,           m = 0, 1, …, M,

           p = 0, 1, ..., P,        m = 0, 1, …, M,

где  — компонента сеточной функции, относящаяся к узлу    — шаг по времени,   h — шаг по координате, 

2.3. Пример разностной задачи (разностной схемы)

Для рассмотренной дифференциальной задачи одна из возможных разностных схем имеет следующий вид:



p = 0, 1, …, P – 1;                m = 1, 2, …, M – 1;

                        m = 0, 1, …, M;                               (11.1a)

                            p = 1, 2, …, P;

                           p = 1, 2, …, P.

2.4. Шаблон разностной схемы

Рассмотренная разностная схема при заданных m и p связывает значения решения в четырех точках сетки, которые образуют конфигурацию, называемую шаблоном схемы.

2.5. Спектральный признак устойчивости

Для широкого класса эволюционных (зависящих от времени) задач исследование устойчивости можно осуществить с помощью спектрального признака, который в случае разностной задачи с постоянными коэффициентами, состоит в следующем.

Заменяем правую часть разностного уравнения в (11.1a) нулем, краевую задачу — задачей Коши, функцию  — гармоникой  и ищем решение в виде



(для задач с одной пространственной переменной),  — произвольное число, 

Для устойчивости разностной схемы необходимо, чтобы спектр  лежал в круге  где c не зависит от . Подставляя  в рассмотренное разностное уравнение, получим:



или



Разностная схема устойчива, если выполнено неравенство  т. е. когда , h выбраны так, что 

2.6. Шеститочечная параметрическая схема

Сеточный шаблон: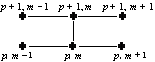



Разностная схема:





p = 0, 1, …, P – 1;                m = 1, 2, …, M – 1;

                        m = 0, 1, …, M;

                            p = 1, 2, …, P;

                           p = 1, 2, …, P.

где  — параметр схемы.

 = 0 — явная четырехточечная схема;

 = 1 — неявная четырехточечная схема;

 = 1/2 — схема Кранка–Николсона.

Метод решения полученной системы линейных уравнений с матрицей трехдиагональной структуры — прогонка.

Порядок аппроксимации:

 = 1/2:                                  

 = 0; 1:                                 

 = 1/6:                                  

Введем обозначения

                              

Схема устойчива при любых К, если   1/2; при  схема устойчива, если

2.7. Схема Франкела–Дюфорта

Сеточный шаблон:



Разностная схема:



p = 1, 2, …, P – 1;                m = 1, 2, …, M – 1;

                        m = 0, 1, …, M;

                            p = 1, 2, …, P;

                           p = 1, 2, …, P.

Значения функции на втором слое по времени рассчитываются по явной центральной четырехточечной схеме. Значение сеточной функции на верхнем временном слое p + 1 рассчитывается по ее значениям на двух предыдущих нижних слоях: p и p – 1.

Порядок аппроксимации: 

Cхема устойчива при любых  

2.8. Схема Ричардсона

Сеточный шаблон:



Разностная схема:



p = 1, 2, …, P – 1;                m = 1, 2, …, M – 1;

                        m = 0, 1, …, M;

                            p = 1, 2, …, P;

                           p = 1, 2, …, P.

Значения сеточной функции на втором слое по времени рассчитываются по явной центральной четырехточечной схеме. Значение сеточной функции на верхнем временном слое p + 1 рассчитывается по ее значениям на двух предыдущих нижних слоях p и p – 1.

Порядок аппроксимации: 

Cхема неустойчива при любых K.

2.9. Явная центральная четырехточечная схема

Сеточный шаблон:



Разностная схема:



p = 0, 1, …, P – 1;                m = 1, 2, …, M – 1;

                        m = 0, 1, …, M;

                            p = 1, 2, …, P;

                           p = 1, 2, …, P.

Значение сеточной функции на верхнем временном слое p + 1 рассчитывается по ее значениям на нижнем слое p.

Порядок аппроксимации: 

Cхема устойчива при 

2.10. Схема Алена–Чена

Сеточный шаблон:



Разностная схема:



p = 0, 1, …, P – 1;                m = 1, 2, …, M – 1;

                        m = 0, 1, …, M;

                            p = 1, 2, …, P;

                           p = 1, 2, …, P.

Значения сеточной функции на верхнем временном слое находятся по ее значениям на нижнем слое, поскольку разностное уравнение разрешается относительно 

Порядок аппроксимации: 

Схема устойчива при любых K.

2.11. Нецентральная явная схема

Сеточный шаблон:



Разностная схема:



p = 0, 1, …, P – 1;                m = 2, 3, …, M;

                        m = 0, 1, …, M;

                            p = 1, 2, …, P;

                           p = 1, 2, …, P.

Значение сеточной функции на верхнем временном слое p + 1 рассчитывается по ее значениям на нижнем слое p (значения сеточной функции в точках {m = 1; p = 1, 2, …, P} рассчитываются по шеститочечной параметрической схеме при  = 1).

Порядок аппроксимации: О().

Схема неустойчива при любых K.

2.12. Схема Саульева

Сеточный шаблон:



Разностная схема:





p = 0, 1, …, P – 2;                m = 1, 2, …, M – 1;

начальные и граничные условия в такой схеме реализуют следующим образом:

                        m = 0, 1, …, M;

                            p = 1, 2, …, P;

                           p = 1, 2, …, P.

Алгоритм численного решения задачи — «бегущий счет»: слева направо — первый этап, справа налево — второй.

Порядок аппроксимации: 

Схема устойчива при любых K.