Билеты мун зачета МА11 База и Профиль 2021. Билеты к зачету по математике в 11 классе рекомендованные для обучающихся, которые сдают егэ профильного уровня
 Скачать 0.94 Mb. Скачать 0.94 Mb.
|
|
БИЛЕТЫ К ЗАЧЕТУ ПО МАТЕМАТИКЕ В 11 КЛАССЕ рекомендованные для обучающихся, которые сдают ЕГЭ профильного уровня . В данном комплекте предложены материалы для проведения устного экзамена по математике в форме ответа по билетам для итоговой аттестации выпускников XI классов общеобразовательных учреждений, изучавших математику на базовом и профильном уровнях. Представленные экзаменационные билеты для итоговой аттестации выпускников старшей школы не нацелены на какую-либо из авторских программ или конкретный учебник, используемый в школе. Они составлены с учетом обязательных минимумов содержания основного общего и среднего (полного) общего образования, а также государственных стандартов основного общего и среднего (полного) общего образования (приказ Минобразования России от 05.03.2004 № 1089). В комплект входят 11 билетов, каждый из которых включает в себя один вопрос по конкретному разделу курса математики, знание которого обучающимся необходимо для сдачи ЕГЭ профильного уровня, и пять заданий ЕГЭ преимущественно по теме билета . Представленные 11 билетов можно использовать для аттестации выпускников. Все билеты имеют одну и ту же структуру: теоретический вопрос и пять задач разного уровня сложности. Примерное время, отводимое на подготовку ученика к ответу, – 45-90 минут. Билеты для проведения муниципального публичного зачёта по математике в 11 классах Билет №1 Основные тригонометрические тождества. Формулы приведения. Привести примеры. Найдите значение выражения : а) в) 3. Решите уравнения: а)  б) б)  в) в)  4. а) Решите уравнение б) Укажите корни этого уравнения, принадлежащие отрезку 5. Решите неравенство: 6. В прямоугольном треугольнике ABC точки M и N — середины гипотенузы AB и катета BC соответственно. Биссектриса угла BAC пересекает прямую MN в точке L. а) Докажите, что треугольники AML и BLC подобны. б) Найдите отношение площадей этих треугольников, если Билет №2 Формулы сложения. Формулы двойного угла. Привести примеры. Найдите значение выражения: а) В) 3. Решите уравнения: а)  б) б)  в) в)  4. а) Решите уравнение: б) Определите, какие из его корней принадлежат отрезку 5. Решите неравенство 6. На сторонах AD и BC параллелограмма ABCD взяты соответственно точки M и N, причём M — середина AD, а BN : NC = 1 : 3. а) Докажите, что прямые AN и AC делят отрезок BM на три равные части. б) Найдите площадь четырёхугольника, вершины которого находятся в точках С, N и точках пересечения прямой BM c прямыми AN и AC, если площадь параллелограмма ABCD равна 48. Билет №3 1. Правила вычисления производных. Производные тригонометрических функций. Привести примеры. 2. а)На рисунке изображен график производной функции , определенной на интервале 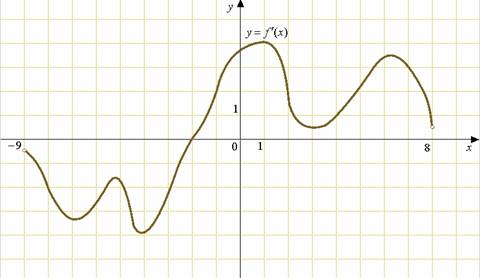 б) Материальная точка движется прямолинейно по закону в) Материальная точка M начинает движение из точки A и движется по прямой на протяжении 12 секунд. График показывает, как менялось расстояние от точки A до точки M со временем. На оси абсцисс откладывается время t в секундах, на оси ординат — расстояние s. Определите, сколько раз за время движения скорость точки M обращалась в ноль (начало и конец движения не учитывайте). 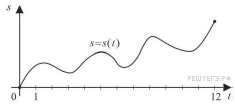 3. Решите уравнения: а)  б) б)  в) в)  4. а) Решите уравнение б) Укажите корни этого уравнения, принадлежащие отрезку 5. Решите неравенство 6.. Медианы AA1, BB1 и CC1 треугольника ABC пересекаются в точке M. Известно, что AC = 3MB. а) Докажите, что треугольник ABC прямоугольный. б) Найдите сумму квадратов медиан AA1 и CC1, если известно, что AC = 10. Билет №4 1. Иррациональные уравнения. Алгоритм решения иррациональных уравнений. Привести примеры. 2 Найдите значение выражения :а) б) в) 3. Решите уравнения: а) 4.. а) Решите уравнение б) Найдите все корни этого уравнения, принадлежащие отрезку 5. Решите неравенство 6. Точка Е — середина стороны BС квадрата АВСD. Серединные перпендикуляры к отрезкам АЕ и ЕС пересекаются в точке O. а) Докажите, что б) Найдите Билет №5 1. Логарифмы и их свойства. Привести примеры. 2. Решите уравнения: а) 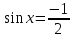 б) б) 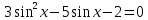 в) в) 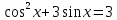 3. Найдите значение выражения: а)  б) б)  в) в)  4. а) Решите уравнение б) Укажите корни этого уравнения, принадлежащие отрезку 5. Решите неравенство 6. В трапеции ABCD с основаниями ВС и AD углы ABD и ACD прямые. а) Докажите, что АВ = CD. б) Найдите AD, если AB = 2, BC = 7. Билет №6 1. Корень п-й степени и его свойства. Привести примеры. 2. Найдите производную функции и вычислите: а) 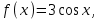 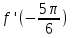 б) б) 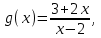 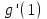 в) 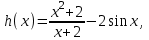 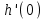 3. Решите уравнения: а)  б) б)  в) в)  4. Решите уравнение 5. Решите неравенство: 6. В треугольнике ABC угол ABC тупой, H — точка пересечения продолжений высот, угол AHC равен 60°. а) Докажите, что угол ABC равен 120°. б) Найдите BH, если Билет №7 1. Степень с рациональным показателем. Привести примеры. 2. Найдите производную функции и вычислите: а) 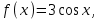 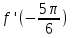 б) б) 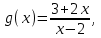 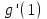 в) 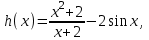 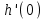 3. Решите уравнения: а)  б) б)  в) в)  4. а) Решите уравнение 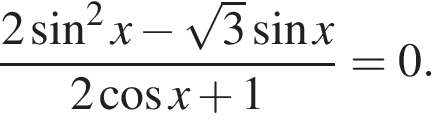 б) Найдите все корни этого уравнения, принадлежащие отрезку 5. Решите неравенство 6. Дана трапеция ABCD с основаниями AD и BC. Диагональ BD разбивает её на два равнобедренных треугольника с основаниями AD и CD. а) Докажите, что луч AC — биссектриса угла BAD . б) Найдите CD, если известны диагонали трапеции: AC = 15 и BD = 8,5. Билет №8 1. Алгоритм решения показательных уравнений и неравенств. Привести примеры. 2. Решите уравнения: а) 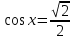 б) б) 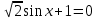 в) в) 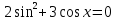 3. Найдите значение выражения: а)  б) б)  в) в)  4. Решите уравнение 5. Решите неравенство: 6. Точки B1 и C1 лежат на сторонах соответственно AC и AB треугольника ABC, причём AB1 : B1C = AC1 : C1B. Прямые BB1 и CC1 пересекаются в точке O. а) Докажите, что прямая AO делит пополам сторону BC. б) Найдите отношение площади четырёхугольника AB1OC1 к площади треугольника ABC, если известно, что AB1 : B1C = AC1 : C1B = 1 : 4. Билет №9 1. Алгоритм решения логарифмических уравнений и неравенств. Привести примеры. 2. Решите уравнения: а) 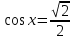 б) б) 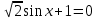 в) в) 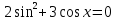 3. Найдите значение выражения: а)  б) б) 4. Решите уравнение |
