Математические методы в психологии. Исправлено Математические методы. Были протестированы две группы студентов. Тест содержал 60 вопросов. Указано число правильных ответов каждого участника теста

• Название: Были протестированы две группы студентов. Тест содержал 60 вопросов. Указано число правильных ответов каждого участника теста
• Анкор: Математические методы в психологии
• Дата: 18.04.2023
• Размер: 45.77 Kb.
• Имя файла: Исправлено Математические методы.docx
• Тип: Задача; #1070677

Автономная некоммерческая организация высшего образования «МОСКОВСКИЙ МЕЖДУНАРОДНЫЙ УНИВЕРСИТЕТ»

Кафедра экономики и управления Форма обучения: заочная

ВЫПОЛНЕНИЕ

ПРАКТИЧЕСКИХ ЗАДАНИЙ

ПО ДИСЦИПЛИНЕ

МАТЕМАТИЧЕСКИЕ МЕТОДЫ В ПСИХОЛОГИИ


Группа Лх19П191


Студент

М.Н. Ершова

МОСКВА 2023

Задача №1

Были протестированы две группы студентов. Тест содержал 60 вопросов. Указано число правильных ответов каждого участника теста.
Можно ли утверждать, что одна из групп превзошла другую группу по результатам теста?
Группа 1: 55, 45, 42, 40
Группа 2: 46, 41, 38, 35, 34

Решение.
Проранжируем представленную таблицу. При ранжировании объединяем две выборки в одну. Ранги присваиваются в порядке возрастания значения измеряемой величины, т.е. наименьшему рангу соответствует наименьший балл. Заметим, что в случае совпадения баллов для нескольких учеников ранг такого балла следует считать, как среднее арифметическое тех позиций, которые занимают данные баллы при их расположении в порядке возрастания.
Используя предложенный принцип ранжирования, получим таблицу рангов.

X Ранг X Y Ранг Y
34 0
35 40
38 42
41 45
46 55
Сумма 0 Сумма 0
Этих данных достаточно, чтобы воспользоваться формулой расчёта эмпирического значения критерия:
u_emp=5*5+ ⁵⁽₂⁵⁺¹⁾ - 0=40
Гипотеза H0 о незначительности различий между выборками принимается, если Uкр < uэмп. В противном случае H0 отвергается и различие определяется как существенное.
где Ukp - критическая точка, которую находят по таблице Манна-Уитни.
Найдем критическую точку Ukp.
По таблице находим Ukp(0.05) = 9
По таблице находим Ukp(0.01) = 4
Так как Ukp < uэмп — принимаем нулевую гипотезу с вероятностью 95%; различия в уровнях выборок можно считать не существенными
Ответ: Группа 1 не превосходит группу 2 по результатам теста

Задача №2

Проведено выборочное обследование частных психологических кабинетов города. Имеются следующие данные о величине посещаемости для 50 кабинетов города (xi – количество клиентов в месяц, млн. руб.; ni – числом кабинетов).

xi	30-80	80-130	130-180	180-230	230-280	280-330
ni	15	13	7	5	3	2

xi	55	105	155	205	255	305
ni	15	13	7	5	3	2

Найти: а) среднее X, среднеквадратичное отклонение S и коэффициент V; б) построить гистограмму и полигон частот.

Решение:
Перейдем к простому вариационному ряду, выбирая в качестве
значений середины интервалов. Получим:
Найдем необходимые числовые характеристики на основе
последовательных расчетов:

xi	55	105	155	205	255	305	
ni	15	13	7	5	3	2	45
xi ni	825	1365	1085	1025	762	610	5672
(xi-X)2 * ni	75615	5733	5887	31205	49923	64082	232445

Среднее: X = (1/n) * ( x_i n_i) = (1/45) * 5672 = 126

Дисперсия: S² = (1/n) *  ((x_i - X)² * n_i) = (1/50) * 232445 = 4649

Среднеквадратичное отклонение: S =  S²  68,184

Коэффициент вариации:

V = (S/X) * 100% = (68,184/126) * 100% = 54,11%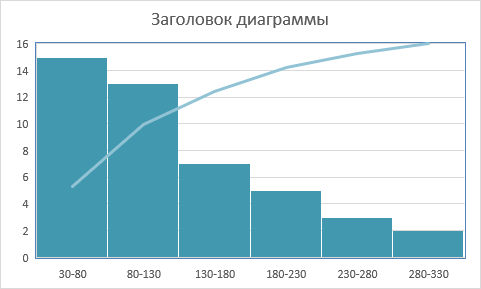


Задача №3

Психолог просит супругов проранжировать девять личностных черт, имеющих определяющее значение для семейного благополучия. Задача заключается в том, чтобы определить, в какой степени совпадают оценки супругов по отношению к ранжируемым качествам. Заполните таблицу и, посчитав коэффициент ранговой корреляции Спирмена, ответьте на поставленный вопрос.

Черты личности Муж Жена Ответственность 6 8 Общительность 4 6 Сдержанность 1 2 Выносливость 2 1 Жизнерадостность 3 4 Терпеливость 5 3 Решительность 7 5 Оптимизм 8 7 Надежность 9 9 ранг X, dx ранг Y, dy (dx - dy) 2 6 8 4 4 6 4 1 2 1 2 1 1 3 4 1 5 3 4 7 5 4 8 7 1 9 9 0 45 45 45

Проверка правильности составления матрицы на основе исчисления контрольной суммы:

Сумма по столбцам матрицы равны между собой и контрольной суммы, значит, матрица составлена правильно.
По формуле вычислим коэффициент ранговой корреляции Спирмена.


Согласованность между мнениями супругов сильная и прямая



Задача 4.

Дана выборка: 5,15,15,10,20,20,5,10,20,15. Требуется:
а) Построить статистический ряд распределения частот и полигон частот;
б) Построить вариационный ряд;
в) Найти оценки математического ожидания и дисперсии;
г) Найти выборочные моду, медиану, коэффициент вариации, коэффициент асимметрии.
Решение.
Упорядочим значения по возрастанию

5	5	5	10	10	15	20	20	20	20

Найдем количество вхождений каждого значения, получим ряд распределения частот, по которому построим полигон частот.

xi ni 5 2 10 2 15 3 20 3

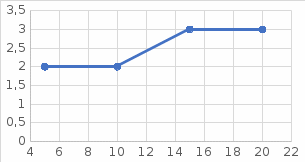Промежуточные вычисления:

xi	ni	xi ni	(xi-X)2 * ni	(xi-X)3 * ni
5	2	10	144,5	-1228,25
10	2	20	24,5	-85,75
15	3	45	6,75	10,125
20	3	60	126,75	823,875
	10	135	302,5	-480

Найдем выборочное среднее: X = (1/n) *  x_i n_i = (1/10)*135 = 13,5
Найдем исправленную дисперсию (несмещенную оценку для
дисперсии по выборке):
S² = (1/n-1) *  (x_i-X)² *n_i = (1/9)*302,5  33,611
Исправленное среднеквадратичное отклонение: S  5,797
Мода – значение с наибольшей частотой: Мо = 20 .
Медиана – значение в середине ряда, в данном случае среднее арифметическое двух серединных значений: Ме = (10+15)/2 = 12,5
Коэффициент вариации: V = (S/X)*100% = (5,797/13,5)*100%  42,94%
Коэффициент асимметрии:
As = [ (1/n) *  (x_i-X)²n_i ]/s³ = -48/5,797³  -0,289