Проверен. Биномиальные деревья. Вывод формулы КоксаРоссРубинштейна. Найти цену c опциона покупателя европейского типа
 Скачать 104.89 Kb. Скачать 104.89 Kb.
|
|
Министерство образования и науки Российской Федерации Федеральное государственное автономное образовательное учреждение высшего образования «Национальный исследовательский Томский политехнический Университет»  Центр цифровых образовательных технологий 01.03.02 Прикладная математика и информатика ____________________________ работа по дисциплине: Творческий проект Тема работы Биномиальные деревья. Вывод формулы Кокса-Росс-Рубинштейна. Найти цену C опциона покупателя европейского типа
Томск – 2022 ОглавлениеБинарные деревья. 3 Одноступенчатая биномиальная модель 4 Двуступенчатая биномиальная модель 5 Список литературы 7 Мелковато, еле рассмотрел Бинарные деревья.Никаких точек в заголовках Одним из наиболее распространенных и полезных методов оценки фондовых опционов является построение биномиального дерева (binomial tree), то есть диаграммы, демонстрирующей разные варианты изменения цены акции в течении срока действия опциона. Этот метод основан на предположении, что цена акции подчиняется законам случайного блуждания (random walk). На каждом шаге по времени существует определенная вероятность того, что цена увеличится или уменьшится на некую относительную величину. Если величина временного шага стремится к нулю, это приводит к предположению, что цены акций имеют логнормальное распределение, лежащая в основе модели Блэка-Шоулза.[1] Бинарные опционы напоминают рулетку, поскольку работают по принципу «угадал/не угадал». У многих типов бинарных опционов нет привычных нам цен исполнения и номиналов (но есть описанные выше барьеры). Прямое копирование. https://whatisbirga.com/vain_options36.html Это недопустимо даже с указанием авторства (здесь, тем более, оно указано косвенно). Д быть прямая цитата в этом случае. Но если цитаты по объему превосходят авторский текст, то какой смысл ставить свою ФИО как автора: вы же просто перепечатываете чужое. Как и в рулетке, их условия описываются размерами вы плат. Типичным примером такого опциона является условие: заплатив $10 000 сегодня, вы получаете право на выплату вам $25 000, если курс USD/CHF не коснется отметки 1,2000 в течение следующих 5 месяцев. Такой тип опциона называется «касательным»1 . Касательные опционы разделяются на касательные (one touch) и «недотроги» (no touch). Типичным условием касательного опциона будет: заплатив $10 000 сегодня, вы получаете право на выплату в $25 000, если курс USD/CHF коснется отметки 1,2000 в течение следующих 5 месяцев. Другим типом бинарных опционов являются цифровые (digital) опционы. Они совмещают в своем описании обыкновенные опционы и касательные. У них есть номинал, цена исполнения и размер выплат. Они исполняются, если они «при деньгах» на дату истечения опциона. Однако в отличие от обыкновенных опционов величина выплаты по ним фиксированная. Таким образом, если вы купили цифровой опцион 1,2200 кол на доллар США (пут на CHF), то получите $10 000 независимо от того, будет ли курс spot на дату истечения 1,2205 или же 1,2700.[2] В теоретической части постарайтесь не переписывать учебники. И не впадайте в другую крайность – ваш учебник еще рано писать. -10 б за плагиат Замечу еще раз – выдам другую тему, эту проверять уже не буду [2 c, 218] -5б за нарушение всех правил оформления текста Попрано вобще все 1) выплаты по касательным опционам могут произойти в любой момент жизни опциона2 , а по цифровым только в день исполнения опциона; 2) какими бы странными ни казались названия опционов, идеи, лежащие в их основе, очень просты.[2. c, 218] Рассмотрим следующую ситуацию. Предположим что текущая цена акции равна 20 долл, а через три месяца она будет равна либо 22 долл, либо 18 долл, Нас интересует европейского опциона на покупку акции по цене 21 долл, через три месяца. Это заначит, ч то через три месяца цена опциона примет ровно одно из двух значений. Если цена акции будет равна 22 долл, стоимость опциона будет равна одному доллару. Если же цена акции будет равна 18 долл, стоимость опциона будет равна нулю.(рис 1)[1] 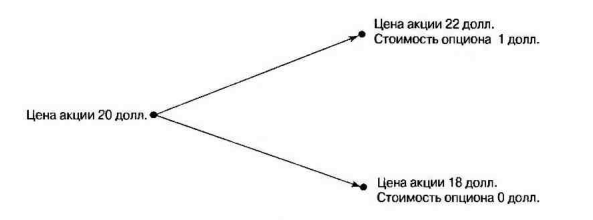 Рис 1название? [1] Одноступенчатая биномиальная модельДля того, что бы определить стоимость опциона предположим, что арбитражные возможности отсутствуют. Создадим инвестиционный портфель состоящий из акций и опциона так чтобы стоимость портфеля через три месяца была точно определенно. Когда цена акции равна S0 и текущая стоимость фондового опциона – f. Предположим что за время действия опциона T либо может подняться либо до величины S0u, где u > 1, либо упасть до уровня S0d, где d < 1. Пропорциональное увеличение цены акции равно u -1, а пропорциональное уменьшение -d-1. Если цена акции увеличится до величины S0u, будем считать что опцион приносит прибыль fu, если же цена акции снижается до уровня S0d, будем считать что опцион приносит прибыль – fd Если цена акции растет то стоимость портфеля равна 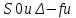 Если же цена падает то Если же цена падает то 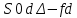 Приравнивая их получаем Приравнивая их получаем 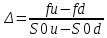 (1) (1)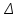 -является отношением изменения цены опциона к изменению цены акции. Буквой r обозначим безрисковую процентную ставку тогда стоимость портфеля -является отношением изменения цены опциона к изменению цены акции. Буквой r обозначим безрисковую процентную ставку тогда стоимость портфеля 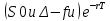 Стоимость создания равна Стоимость создания равна 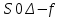 отсюда следует отсюда следует 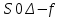 = = 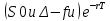 то есть то есть 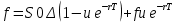 подставляя в это выражение значение подставляя в это выражение значение 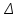 из формулы (1) получаем из формулы (1) получаем 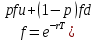 , (2) , (2)где 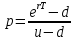 Обозначения к формулам не являются формулами, если они не супергромоздкие Формулы 2 и 3 оценивают опцион, при использовании одноступенчатой биномиальной модели. Двуступенчатая биномиальная модельОбозначим цену акции в первый момент времени S0. В каждый из выбранных моментов времени цена может либо увеличится на число S0u либо уменьшится на число S0d. Цены опциона указаны рядом с узлами дерева(Стоимость опциона через два временных шага обозначается как fuu). Допустим, что безрисковая процентная ставка r%. a длинна шага по времени равна 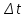 лет. лет. Рис 2 Цена акции и цена опциона в общем двуступенчатом дереве[2] Так как длина шага по времени равна  то формулы (1) и (2) записываются. то формулы (1) и (2) записываются.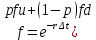 (4), (4), 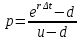 (5) повторно используя формулу (2) (5) повторно используя формулу (2) 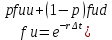 ](6), ](6),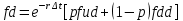 (7), (7), 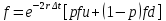 (8) (8)Подставляя формулы (6) и (7) в формулу (8) получаем 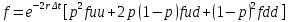 (9) (9)Величины 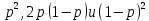 представляют собой вероятность попасть в верхний, средний и нижний узел соответственно. Цена опциона равна его ожидаемому выигрышу в риск-нейтральном мире с дисконтом на величину безрисковой процентной ставки.[2] представляют собой вероятность попасть в верхний, средний и нижний узел соответственно. Цена опциона равна его ожидаемому выигрышу в риск-нейтральном мире с дисконтом на величину безрисковой процентной ставки.[2]Добавление в биномиальное дерево дополнительные уровни не нарушает принцип риск-нейтральности. Цена опциона всегда равна ожидаемому выигрышу в риск-нейтральном мире, дисконтированному по безрисковой процентной ставке. Список литературы1) Опционы, фьючерсы и другие производные финансовые инструменты | Халл Джон К. 2)Саймон Вайн – Опционы. Полный курс для профессионалов -2б за неправильно оформленные ссылки в списке литературы, неверно вы упоминаете литературу в тексте (не там, не так) Итого 13 б | ||||||||||||||||||||||||||||||||||||
