Бир жинсли блмаган ютилиш ёки манбааси блган соада чизисиз фильтрлаш масаласини сонли моделлаштириш

• Название: Бир жинсли блмаган ютилиш ёки манбааси блган соада чизисиз фильтрлаш масаласини сонли моделлаштириш
• Дата: 29.05.2022
• Размер: 0.67 Mb.
• Имя файла: 4. mavzu.docx
• Тип: Документы; #554982
• страница: 4 из 4

, ,

ҳоли учун.

Параметрларнинг хар ҳил қийматлари учун баъзи бир сонли натижаларни таққослашларни келтирамиз. 6.5 жадвалда N=2 учун параметрларнинг σ р=0.1, β=4, α=1, m=0, T=2 қийматларидаги ечимлари келтирилган. 6.6 жадвалда N=2 учун параметрларнинг р=0.1, β=4, α=1, m=1, T=2 қийматларидаги ечимлари келтирилган. Тўр етарлича майда: L/10, - даги фронт қиймати. t бўйича ҳисоблашлар қадам билан ўтказилган. Бир нечта фронтга яқин нуқталардан ташқари хамма ерда ҳисобланган ечимнинг аниқ ечимдан фарқи 10^-2 дан ошмайди. Ҳисоблашлар шарт бажарилгунча амалга оширилган. Итерациялар сони .

Мос равишда 6.5 хамда 6.6 расмларда m=0 ва m=1 қийматлар учун сонли натижаларни таққослаш мумкин.


6.5 жадвал. Параметрларнинг p=0.1, β=4, α=1, m=0, T=2 қийматлари учун ҳисоблаш натижалари

t	Сон-ли нат. (0;0)	Аниқ қий- мат (0;0)	Хато-лик		Сон-ли нат. (1;5)		Аниқ қий- мат (1;5)	Хато-лик		Сон-ли нат. (5;5)	Аниқ қий- мат (5;5)			Хато-лик		Итарация сони	фронт
0	0,79	0,79		0	0,02	0,02		0	0			0	0		1		5,192
0,26	0,76	0,76		0,003	0,02	0,03		0	0			0	0		6		5,555
0,52	0,73	0,73		0	0,03	0,04		0,01	0			0	0		3		5,894
0,78	0,7	0,7		0,002	0,04	0,06		0,02	0			0	0		6		6,213
1,04	0,68	0,68		0	0,05	0,07		0,01	0			0	0		3		6,516
1,3	0,66	0,66		0,001	0,06	0,08		0,03	0			0	0		6		6,805
1,56	0,64	0,64		1E-16	0,07	0,1		0,02	0			0	0,01		3		7,08
1,82	0,63	0,62		7E-04	0,08	0,11		0,03	0,01			0	0,01		6		7,345
2,08	0,61	0,61		0	0,09	0,12		0,03	0,01			0	0,01		3		7,6
2,34	0,6	0,6		5E-04	0,09	0,13		0,04	0,01			0	0,02		6		7,847
2,6	0,58	0,58		0	0,11	0,14		0,03	0,01			0	0,02		3		8,085
2,86	0,57	0,57		4E-04	0,11	0,15		0,04	0,01			0	0,02		6		8,316
3,12	0,56	0,56		0	0,12	0,16		0,03	0,01			0	0,03		3		8,54
3,37	0,55	0,55		3E-04	0,12	0,17		0,04	0,02			0	0,03		6		8,758
3,63	0,54	0,54		0	0,14	0,17		0,04	0,02			0,1	0,04		3		8,971
3,89	0,54	0,54		3E-04	0,14	0,18		0,04	0,02			0,1	0,04		6		9,178
4,15	0,53	0,53		0	0,15	0,19		0,04	0,02			0,1	0,05		3		9,38
4,41	0,52	0,52		2E-04	0,15	0,19		0,05	0,02			0,1	0,05		6		9,578
4,67	0,51	0,51		0	0,16	0,2		0,04	0,02			0,1	0,05		3		9,771
4,93	0,51	0,51		2E-04	0,16	0,2		0,05	0,02			0,1	0,06		6		9,961
5,19	0,5	0,5		0	0,16	0,21		0,04	0,02			0,1	0,06		3		10,15

6.6 жадвал. Параметрларнинг p=0.1, β=4, α=1, m=1, T=2 қийматлари учун ҳисоблаш натижалари

t	Сон-ли нат. (0;0)	Аниқ қий- мат (0;0)	Хато-лик	Сон-ли нат. (1;5)	Аниқ қий- мат (1;5)	Хато-лик	Сон-ли нат. (5;5)	Аниқ қий- мат (5;5)	Хато-лик	Итарация сони	фронт
0	0,79	0,79	0	0,02	0	0,02	0	0	0	1	6,74
0,34	0,76	0,76	0,003	0,02	0	0,02	0	0	0	7	7,71
0,67	0,73	0,73	0	0,03	0	0,03	0	0	0	3	8,68
1,01	0,7	0,7	0,002	0,01	0	0,01	0	0	0	7	9,65
1,35	0,68	0,68	0	0,03	0	0,03	0,01	0	0,01	3	10,6
1,68	0,66	0,66	0,001	0,02	0	0,02	0,01	0	0,01	7	11,6
2,02	0,64	0,64	1E-16	0,03	0	0,03	0,01	0	0,01	3	12,5
2,36	0,63	0,62	7E-04	0,02	0	0,01	0,01	0	0,01	7	13,5
2,7	0,61	0,61	0	0,03	0	0,02	0,01	0	0,01	3	14,4
3,03	0,6	0,6	5E-04	0,02	0	0,01	0,01	0	0,01	7	15,4
3,37	0,58	0,58	0	0,03	0,01	0,02	0,01	0	0,01	3	16,3
3,71	0,57	0,57	4E-04	0,02	0,01	0,01	0,01	0	0,01	7	17,3
4,04	0,56	0,56	0	0,03	0,01	0,02	0,01	0	0,01	3	18,2
4,38	0,55	0,55	3E-04	0,02	0,01	0,01	0,01	0	0,01	7	19,2
4,72	0,54	0,54	0	0,03	0,02	0,01	0,01	0	0,01	3	20,1
5,05	0,54	0,54	3E-04	0,02	0,02	0	0,01	0	0,01	7	21,1
5,39	0,53	0,53	0	0,03	0,02	0,01	0,01	0	0	3	22
5,73	0,52	0,52	2E-04	0,03	0,03	0	0,01	0,01	0	7	22,9
6,07	0,51	0,51	0	0,04	0,03	0,01	0,01	0,01	0	3	23,9
6,4	0,51	0,51	2E-04	0,03	0,03	0	0,01	0,01	0	7	24,8
6,74	0,5	0,5	0	0,04	0,04	0	0,01	0,01	0	3	25,7

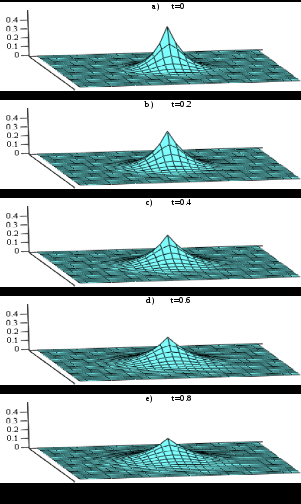
6.5 расм Параметрларнинг p=0.1, 6.6 расм Параметрларнинг p=0.1,

β=4, α=1, m=0, T=2: a) t=0; b) t=0,2; β=4, α=1, m=1, T=2. a) t=0; b) t=0,2;

c) t=0,4; d) t=0,6; e) t=0,8. c) t=0,4; d) t=0,6; e) t=0,8.

қийматлари учун ҳисоблаш қийматлари учун ҳисоблаш натижалари натижалари

6.7 хамда 6.8 расмларда р=0.1 ва р=0.9 қийматлар учун сонли натижаларни таққослаш мумкин.


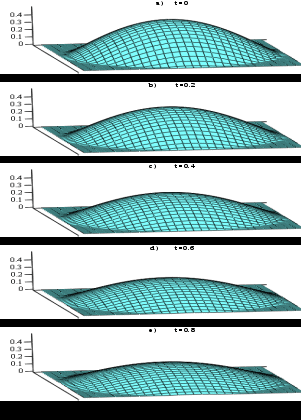
6.7 расм Параметрларнинг p=0.1, 6.8 расм Параметрларнинг p=0.9,

β=4, α=1, m=0, T=2: a) t=0; b) t=0,2; β=4, α=1, m=0, T=2. a) t=0; b) t=0,2;

с) е=0,4. в) е=0,6. у) е=0,8. с) е=0,4. в) е=0,6. у) е=0,8.

қийматлари учун ҳисоблаш қийматлари учун ҳисоблаш натижалари натижалари
Кўп сонли экспериментларнинг келтирилган натижалари шуни кўрсатдики, шахсий компьютерларни фильтрлаш масалаларида қўллаш, машина вақтини кўп сарфламаган холда, киритилувчи қийматларни ўзгартиришнинг кенг диапазони учун аниқлик даражаси катта бўлган натижалар олиш имконини берар экан. Экспериментлар натижаларидан кўринадики, кўп холларда автомодел ва тақрибий-автомодел тенгламаларнинг ечимлари кўрилаётган тенгламанинг аниқ ёки тақрибий ечими бўлар екан.

Қуйидаги автомодел тенгламани ечишда
, (6.78)
қуйидагича чизиқсиз тенгламани ечиш зарурати пайдо бўлади

(6.79)
(6.42) алгебраик тенгламани ечиш учун Ньютон итерацион усули қўлланилди. деб фараз қилган холда сонли ҳисоблар бажарилди ва , , , , бўлган хол учун ечимнинг мавжудлиги исбот қилинди. Параметрларнинг хар ҳил қийматлари учун ҳисоблаш эксперименти ўтказилди.