Бир жинсли блмаган ютилиш ёки манбааси блган соада чизисиз фильтрлаш масаласини сонли моделлаштириш

• Название: Бир жинсли блмаган ютилиш ёки манбааси блган соада чизисиз фильтрлаш масаласини сонли моделлаштириш
• Дата: 29.05.2022
• Размер: 0.67 Mb.
• Имя файла: 4. mavzu.docx
• Тип: Документы; #554982
• страница: 2 из 4

Огохлантириш. Хамма рақамли ҳисоблашларда деб олинган.

(6.66) да қуйидагича белгилашлар киртамиз:

1) Пикар усули учун
, ,

, , , .

2) махсус усул учун
, ,

, , , .

3) Ньютон усули учун
, ,

, , , .
Қуйидагича белгилашлар киритишни келишиб оламиз
, .
(6.66) айирмали тенгламани
, . (6.67)
кўринишда ёзиб олиш мумкин.

(6.67) тенгламалар системасини сонли ечиш учун прогонка усулини қўлланади.

Энди соҳада (6.62) тенгламани икки ўлчовли ҳолда кўриб чиқамиз ( )
(6.68)
бошланғич шартлар
. (6.69)

соҳасида ( ) бўйича ва қадамлар билан тенг ўлчовли :
,
ва вақтинчали
, . (6.70)
тўрлар қурамиз.

(6.68)-(6.69) масаласини сонли ечиш учун Писмен-Речфорд схемаси деб аталувчи ўзгарувчан йўналишлар усули қўлланади
, (6.71)

.
Чегаравий масалани қуйидаги кўринишда қайта ёзиб оламиз
, (6.72)
бу ерда .

Қуйидагича белгилашлар киритамиз
(6.73)

шунингдек

, ,
белгилашга келишиб оламиз.

Хосил бўлган (6.71) чизиқсиз тенгламалар системасини ечиш учун итерацион усул қўллаймиз ва қуйидаги схемани ҳосил қиламиз
, (6.74)

, (6.4.1.35)

.
(6.74)да қуйидагича белгилашлар киритиб
, ,

, , .
Айирмали тенгламани
(6.76)

.
кўринишда ёзиб олиш мумкин.

Мос равишда (6.75) ни
(6.77)
бу ерда

, , , ,
кўринишда ёзиб оламиз.

(6.76) ва (6.77) системаларни сонли ечиш учун прогонка усули қўлланилади. (6.76) тенгламалар системаси сатрлар бўйлаб ечилади ва тўрининг хар бир нуқтасида аниқланади. Сўнгра (6.77) тенгламалар системаси устунлар бўйлаб ни тўрининг хар бир нуқтасида аниқлаган холда ечилади.

қатламдан қатламга ўтишда ҳисоблаш процедураси такрорланади.
4.2. Ҳисоблаш экспериментлари (сонли ҳисоблашлар)
Ушбу бўлимда юқорида кўриб чиқилган масалаларнинг ҳисоблаш натижалари келтирилган. Ўрганилаётган фильтрлаш жараёнининг математик модели қурилиб, олинган ечимларни бахолаш асосида, замонавий дастурлаш воситаларидан фойдаланган холда алгоритм ва дастурлар ишлаб чиқилди. Масалани ечишнинг сонли схемалари келтирилди. Дастурлар Mathcad универсаль математик муҳит тилида ишлаб чиқилди.

Бир жинсли бўлмаган ютилиш ёки манбааси бўлган фильтрлаш жараёнининг бир ва икки ўлчовли холлари учун сонли модели келтирилган. Тенгламада иштирок этадиган параметрларнинг хар ҳил қийматлари учун ҳисоблаш эксперименти натижалари келтрилган. Жараённинг вақт бўйича ўзгариши тасвири шахсий компьютерда Mathcadдан фойдаланган холда моделлаштирилди.

(6.41) тенгламани бир ва икки ўлчовли холлари учун сонли ечиш чоғида кўплаб экспериментлар ўтказилди.

1) Қуйида (6.41)-(6.43) ҳисоблашларнинг натижаларини (буғланиш ҳоли) ҳол учун келтирамиз:

Бошланғич яқинлашиш қуйидаги кўринишда олинган:
,

бу ерда , _, , ,



ҳоли учун.

Параметрларнинг хар ҳил қийматлари учун баъзи бир сонли натижаларни таққослашларни келтирамиз. N=2 учун 6.1 жадвалда параметрларнинг σ=1, β=6, α=1, m=0, T=2 қийматларидаги натижалари келтирилган. N=2 учун 6.2 жадвалда параметрларнинг σ=1, β=6, α=1, m=1, T=2 қийматларидаги натижалари келтирилган. Тўр етарлича майда: L/10, - даги фронт қиймати. t бўйича ҳисоблашлар қадам билан ўтказилган. Бир нечта фронтга яқин нуқталардан ташқари хамма ерда ҳисобланган ечимнинг аниқ ечимдан фарқи 10^-2 дан ошмайди. Ҳисоблашлар шарт бажарилгунча амалга оширилган. Итерациялар сони .

Мос равишда 6.1 хамда 6.2 расмларда m=0 ва m=1 қийматлар учун сонли натижаларни таққослаш мумкин.

6.1 жадвал. Параметрларнинг σ=1, β=6, α=1, m=0, T=2 қийматлари учун ҳисоблаш натижалари.
t		Сон-ли нат. (0;0)		Аниқ қий- мат (0;0)		Хато-лик	Сон-ли нат. (1;5)		Аниқ қий- мат (1;5)		Хато-лик		Сон-ли нат. (5;5)		Аниқ қий- мат (5;5)			Хато-лик		Итарация сони	фронт
0		0,63		0,63		0	0,35		0,35		0		0,08		0,082			0		1	2,512
0,13		0,63		0,62		2E-04	0,33		0,35		0,02		0,1		0,102			0		7	2,561
0,25		0,62		0,62		0	0,35		0,36		0,01		0,11		0,12			0,01		3	2,609
0,38		0,61		0,61		1E-04	0,33		0,37		0,03		0,12		0,136			0,01		7	2,656
0,5		0,61		0,61		0	0,35		0,37		0,02		0,13		0,151			0,02		3	2,702
0,63		0,6		0,6		1E-04	0,34		0,37		0,04		0,14		0,164			0,02		7	2,746
0,75		0,6		0,6		0	0,36		0,38		0,02		0,15		0,176			0,03		3	2,79
0,88		0,59		0,59		1E-04	0,35		0,38		0,04		0,15		0,187			0,03		7	2,832
1		0,59		0,59		0	0,36		0,39		0,02		0,16		0,198			0,04		3	2,874
1,13		0,59		0,59		8E-05	0,35		0,39		0,04		0,16		0,207			0,04		7	2,914
1,26		0,58		0,58		0	0,37		0,39		0,02		0,17		0,216			0,05		3	2,954
1,38		0,58		0,58		7E-05	0,36		0,39		0,04		0,17		0,224			0,05		7	2,993
1,51		0,57		0,57		0	0,37		0,4		0,03		0,17		0,231			0,06		3	3,031
1,63		0,57		0,57		6E-05	0,36		0,4		0,04		0,18		0,238			0,06		7	3,069
1,76		0,57		0,57		0	0,37		0,4		0,03		0,18		0,244			0,06		3	3,106
1,88		0,56		0,56		6E-05	0,36		0,4		0,04		0,18		0,25			0,07		7	3,142
2,01		0,56		0,56		0	0,37		0,4		0,03		0,19		0,256			0,07		3	3,178
2,14		0,56		0,56		5E-05	0,37		0,4		0,04		0,19		0,261			0,07		7	3,213
2,26		0,55		0,55		1E-16	0,38		0,4		0,03		0,19		0,266			0,07		3	3,247
2,39		0,55		0,55		4E-05	0,37		0,41		0,04		0,19		0,27			0,08		7	3,281
2,51		0,55		0,55		0	0,38		0,41		0,03		0,2		0,275			0,08		3	3,314
6.2. жадвал. Параметрларнинг σ=1, β=6, α=1, m=1, T=2 қийматлари учун ҳисоблаш натижалари.
T		Сон-ли нат. (0;0)		Аниқ қий- мат (0;0)		Хато-лик	Сон-ли нат. (1;5)		Аниқ қий- мат (1;5)		Хато-лик		Сон-ли нат. (5;5)		Аниқ қий- мат (5;5)			Хато-лик		Итарация сони	фронт
0		0,63		0,63		0	0,07		0,07		0		0		0			0		1	1,5774
0,08	0,63		0,62		2E-04			0,08		0,09		0,008		7E-08		0	0		6		1,6402
0,16	0,62		0,62		0			0,11		0,11		0,004		3E-06		0	0		3		1,7024
0,24	0,61		0,61		1E-04			0,1		0,13		0,023		5E-05		0	0		6		1,764
0,32	0,61		0,61		0			0,13		0,14		0,008		3E-04		0	0		3		1,8251
0,39	0,6		0,6		1E-04			0,13		0,16		0,025		0,001		0	0		7		1,8857
0,47	0,6		0,6		0			0,16		0,17		0,01		0,004		0	0		3		1,9458
0,55	0,59		0,59		1E-04			0,15		0,18		0,027		0,008		0,02	0,01		7		2,0054
0,63	0,59		0,59		0			0,18		0,19		0,012		0,015		0,04	0,02		3		2,0646
0,71	0,59		0,59		8E-05			0,17		0,2		0,028		0,024		0,05	0,03		7		2,1234
0,79	0,58		0,58		0			0,19		0,21		0,014		0,035		0,06	0,03		3		2,1818
0,87	0,58		0,58		7E-05			0,19		0,22		0,028		0,045		0,08	0,03		7		2,2398
0,95	0,57		0,57		0			0,21		0,22		0,015		0,055		0,09	0,03		3		2,2974
1,03	0,57		0,57		6E-05			0,2		0,23		0,028		0,064		0,1	0,04		7		2,3547
1,1	0,57		0,57		0			0,22		0,24		0,016		0,072		0,11	0,04		3		2,4116
1,18	0,56		0,56		6E-05			0,22		0,24		0,028		0,079		0,12	0,04		7		2,4681
1,26	0,56		0,56		0			0,23		0,25		0,016		0,087		0,13	0,04		3		2,5244
1,34	0,56		0,56		5E-05			0,23		0,26		0,028		0,094		0,14	0,04		7		2,5803
1,42	0,55		0,55		1E-16			0,24		0,26		0,017		0,101		0,15	0,04		3		2,636
1,5	0,55		0,55		4E-05			0,24		0,26		0,028		0,107		0,15	0,05		7		2,6913
1,58	0,55		0,55		0			0,25		0,27		0,017		0,114		0,16	0,05		3		2,7464

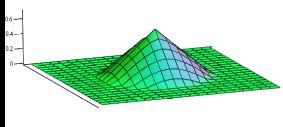
6.1 расм Параметрларнинг σ=1, 6.2 расм. Параметрларнинг σ=1,

β=6, α=1, m=0, T=2 қийматлари β=6, α=1, m=1, T=2 қийматлари учун ҳисоблаш натижалари учун ҳисоблаш натижалари

2) (6.41)-(6.43) ҳисоблаш натижалари (буғланиш холи) холи учун:

Бошланғич яқинлашиш қуйидаги кўринишда олинган:

,

бу ерда

, _,