химия. Бланк выполнения задания 3

• Название: Бланк выполнения задания 3
• Анкор: химия
• Дата: 28.01.2022
• Размер: 36.42 Kb.
• Имя файла: qpe-Himiya-Zadanie-3-reshenie (1).docx
• Тип: Задача; #345231

Бланк выполнения задания № 3

1. Записываются условия задач полностью, без искажений и сокращений.
2. Оформляются подробные решения задач, которые при необходимости подкрепляются формулами, уравнениями реакций, схемами.
3. Записываются ответы к задачам.


Задача 1. Рассчитать массу и объем 10²⁴ молекул азота при температуре 250⁰ С и давлении 170,5 кПа

Решение.

1 моль вещества содержит 6,02*10²³ (число Авогадро) молекул. Тогда 10²⁴ молекул азота содержатся в 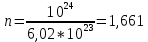моль азота.

Молярная масса азота равна 14,007*2 = 28,01 г/моль. Тогда масса 10²⁴ молекул азота равна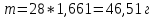



Объём 10²⁴ молекул азота вычислим по уравнению Менделеева – Клапейрона:

PV = nRT, отсюда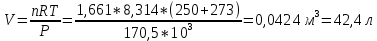


Ответ: 46,51 г; 42,4 л.

Задача 2. В какой массе NаОН содержится столько же эквивалентов, сколько и в 140 г КОН?

Решение.

Молярная масса КОН равна 56 г/моль.

В 140 г КОН содержится 140/56 = 2,50 моль.

Молярная масса NаОН равна 40 г/моль

Тогда масса 2,50 моль NаОН равна

2,50*40 = = 100 г

Ответ: 100 г.

Задача 3. По порядковому номеру элемента составить электронную формулу его атома. Определить природу элемента и валентные электроны. Указать квантовые числа для трех последних электронов. Охарактеризовать местоположение в периодической таблице Д. И. Менделеева. Сравнить электроотрицательности, атомные радиусы и энергии ионизации между элементом и соседними элементами в группе и периоде. Определить состав атома (количество электронов, протонов и нейтронов).

81, 39.

Решение.

В соответствии с принципом наименьшей энергии порядок заполнения атомных орбиталей для элемента 81 имеет вид: 1s²2s²2р⁶3s²3р⁶4s²3d¹⁰4р⁶5s²4d¹⁰5p⁶6s²4f¹⁴5d¹⁰6p¹. Так как последним заполняется p-подуровень, то элемент является p-элементом и его валентными электронами будут 6s²6p¹:

6s

↑↓

6p

↑

Квантовые числа 6s-электронов:

главное n=6;

орбитальное l = 0;

магнитное m_l = 0;

спин s = +1/2 и –1/2 соответственно.

Квантовые числа 6р-электрона:

главное n=6;

орбитальное l =1;

магнитное m_l = –1 (первое из возможных);

спин s = +1/2 или –1/2 соответственно.
Элемент 81 находится в 13 группе 6 периода Периодической системы элементов, это таллий.

В пределах периода энергия ионизации и электроотрицательность возрастают слева направо, поэтому энергия ионизации и электроотрицательность элемента 81 будут выше, чем у элемента 80, но ниже, чем у элемента 82.

В пределах группы энергия ионизации и электроотрицательность убывают сверху вниз, поэтому энергия ионизации и электроотрицательность элемента 81 будут ниже, чем у его соседа сверху, но выше, чем у соседа снизу.

Атомные радиусы в пределах периода снижаются с увеличением заряда ядра, поэтому радиус атома элемента 81 будет выше, чем у элемента 82, но ниже, чем у элемента 80. В пределах группы атомные радиусы возрастают сверху вниз, поэтому радиус атома нашего элемента 81 будет выше, чем у его соседа сверху, но ниже, чем у соседа снизу.

Природный таллий состоит из двух стабильных изотопов: ²⁰⁵Tl  и ²⁰³Tl . 

Число протонов и электронов в атомах обоих изотопов равно порядковому номеру элемента 81.

Число нейтронов равно разности массового числа и заряда ядра (порядкового номера, или числа протонов). Для ²⁰⁵Tl  число нейтронов равно 205 – 81 = 124, а для  ²⁰³Tl  число нейтронов равно 203 – 81 = 122.
В соответствии с принципом наименьшей энергии порядок заполнения атомных орбиталей для элемента 39 имеет вид: 1s²2s²2р⁶3s²3р⁶4s²3d¹⁰4р⁶5s²4d¹. Так как последним заполняется d-подуровень, то элемент является d-элементом и его валентными электронами будут 5s²4d¹:

5s

↑↓

4d

↑

Квантовые числа 5s-электронов:

главное n=5;

орбитальное l = 0;

магнитное m_l = 0;

спин s = +1/2 и –1/2 соответственно.

Квантовые числа 4d-электрона:

главное n=4;

орбитальное l =2;

магнитное m_l = –2 (первое из возможных);

спин s = +1/2 или –1/2 соответственно.

Элемент 39 находится в 3 группе 4 периода Периодической системы элементов, это иттрий.

В пределах периода энергия ионизации и электроотрицательность возрастают слева направо, поэтому энергия ионизации и электроотрицательность элемента 39 будут выше, чем у элемента 38, но ниже, чем у элемента 40.

В пределах группы энергия ионизации и электроотрицательность убывают сверху вниз, поэтому энергия ионизации и электроотрицательность элемента 39 будут ниже, чем у его соседа сверху, но выше, чем у соседа снизу.

Атомные радиусы в пределах периода снижаются с увеличением заряда ядра, поэтому радиус атома элемента 39 будет выше, чем у элемента 40, но ниже, чем у элемента 38. В пределах группы атомные радиусы возрастают сверху вниз, поэтому радиус атома нашего элемента 39 будет выше, чем у его соседа сверху, но ниже, чем у соседа снизу.

Иттрий — моноизотопный элемент, в природе представлен одним стабильным нуклидом ⁸⁹Y. 

Число протонов и электронов в атоме иттрия равно порядковому номеру элемента 39.

Число нейтронов равно разности массового числа и заряда ядра (порядкового номера, или числа протонов). Для иттрия число нейтронов равно 89 – 39 = 50.

Задача 4. Кристаллический хлорид аммония образуется при взаимодействии газообразных аммиака и хлорида водорода. Написать термохимическое уравнение этой реакции и вычислить ее тепловой эффект. Сколько теплоты выделится, если в реакции было израсходовано 10 л аммиака (н. у.)?

Решение.

Термохимическое уравнение реакции:

NH_3(Г) + HCl_(Г) = NH₄Cl_(KP) + Q

Для расчёта теплового эффекта выпишем из термодинамических таблиц стандартные энтальпии образования компонентов реакции:

ΔН⁰_обр (NH_3(г)) = –45,94 кДж/моль

ΔН⁰_обр (HCl_(г)) = –92,31 кДж/моль

ΔН⁰_обр (NH₄Cl_(кр)) = –314,22 кДж/моль

Тогда в соответствии с законом Гесса изменение энтальпии в ходе реакции равно:

ΔН⁰_р = ΔН⁰_обр.NH4Cl + ΔН⁰_обр.Н2 – (ΔН⁰_обр.HCl + ΔН⁰_обр.NH3)

ΔН⁰_р = –314,22 – ((-92,31) + (-45,94)) = -175,97 кДж/моль

Тогда тепловой эффект реакции равен

Q = – ΔН⁰_р = 175,97 кДж/моль

Тогда термохимическое уравнение реакции будет выглядеть так:

NH_3(Г) + HCl_(Г) = NH₄Cl_(KP) + 175,97 кДж/моль

1 моль аммиака при н.у. занимает объём 22,4 л.

Тогда при расходе 10 л аммиака выделится теплоты

175,97*10/22,4 = 78,56 кДж
Ответ: 78,56 кДж

Задача 5. Рассчитать изменение стандартной свободной энергии Гиббса и сделать вывод о направлении процесса при указанной температуре. Рассчитать температуру равной вероятности прямого и обратного процессов. Сделать вывод о направлении процесса выше и ниже этой температуры.

СО_(г) + Н₂О_(г) ↔ СО_2(г) + Н_2(г); 650⁰ С

Решение.

Из термодинамических таблиц выписываем стандартные энтальпии образования и стандартные энтропии веществ:

Функция	СО(г)	Н2О(г)	СО2(г)	Н2(г)
ΔН0обр, кДж/моль	–110,5	–241,8	–393,5	0
S0, Дж/(моль*К)	197,4	189	213,6	130,1

Находим стандартные энтальпию и энтропию реакции

СО_(г) + Н₂О_(г) ↔ СО_2(г) + Н_2(г)

ΔН⁰_р = ΔН⁰_обр.СО2 + ΔН⁰_обр.Н2 – (ΔН⁰_обр.СО + ΔН⁰_обр.Н2О)

ΔН⁰_р = –393,5 + 0 – ((-110,5) + (-241,8)) = -41,2 кДж/моль

ΔS⁰_р = S⁰_СО2 + S⁰_Н2 – (S⁰_СО + S⁰_Н2О)

ΔS⁰_р = 213,6 + 130,1 – (197,4 + 189) = -42,7 Дж/(моль*К)

Находим стандартную энергию Гиббса:

ΔG^о_p = ΔН⁰_р – T* ΔS⁰_р

ΔG^о_p = -41,2 – (650+298)*(-42,7*10^–3) = -0,720 кДж/моль = -720 Дж/моль<0

Следовательно, при температуре 650^оС процесс термодинамически возможен.

Находим равновесную температуру: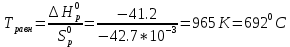



Так как ΔН⁰_р<0 и ΔS⁰_р<0, то прямая реакция возможна при температурах ниже равновесной, то есть прямая реакция возможна до температуры 692 К, а при температуре выше 692 К реакция невозможна.

Ответ: ΔG^о_p = -720 Дж/моль. Реакция возможна при температурах ниже 965 К.

Задача 6. При понижении температуры на 20⁰ С скорость гомогенной реакции понизилась в 10 раз. Как изменится скорость данной реакции при увеличении температуры с 70 до 110⁰ С?

Решение.

Согласно правилу Вант-Гоффа, отношение констант скорости реакции k₂ и k₁, определенных при двух различных температурах Т₂ и Т₁, равно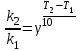

.

Подставим в это уравнение данные из условия задачи и решим его относительно γ: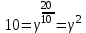

,

Отсюда γ = 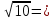3,162

Тогда при увеличении температуры с 70 до 110⁰С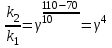

= 10² = 100

Ответ: Скорость реакции увеличится в 100 раз.