ОТВЕТЫ. Блок а раздел 1 Основы гидростатики 1 Основные понятия и определения
 Скачать 1.68 Mb. Скачать 1.68 Mb.
|
|
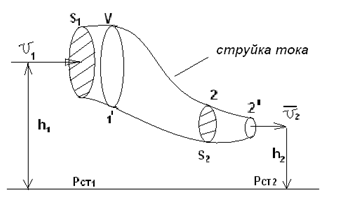
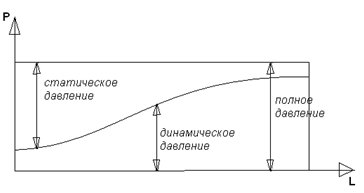
Блок B Уравнение Д. Бернуллли уравнение сохранения и превращения …. жидкости Энергии На рисунке изображен расходомер…. 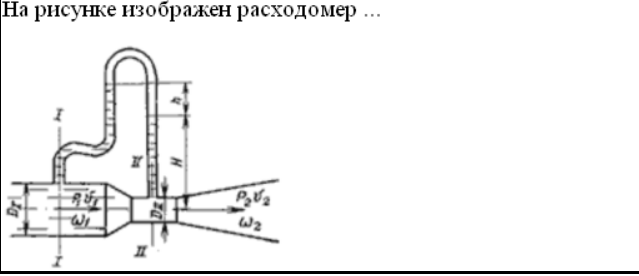 2 Дифференциальные уравнения движения идеальной жидкости Л. Эйлера – это алгебраическая сумма проекций массовых и …. сил Поверхностных 1.Формула 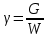 служит для определения… служит для определения…+Удельного веса 2.Формула 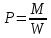 служит для определения… служит для определения…+Плотности 3.Физическое тело,в котором силы межмолекулярного сцепления больше,чем у газообразных,и меньше чем у твердых… +Жидкость 4.Жидкость-физическое тело,в котором силы межмолекулярного сцепления… +больше,чем у газообразных и меньше,чем у твердых 5.Фундаментальное уравнение гидродинамики получил в 1738г… +Д.Бернулли 6.Понятие о вязкости жидкости сформулировал… +И.Ньютон 7.Первый гидравлический закон о воздействии жидкости на погруженное тело сформулировал… +Архимед 8.Раздел гидравлики, изучающий законы движения жидкостей… +Гидродинамика 9.Наука «Гидравлика» -это часть … +механики, изучающей законы равновесия и движения жидкостей(газов) 10.Гидравлика подразделяется на: +Гидродинамику +Гидростатику 11.Гидравлика-прикладная наука,изучающая законы… +Равновесия и движения жидкостей 12.Раздел гидравлики, изучающий законы равновесия жидкостей… +Гидростатика Объем жидкости или газа может изменять свою форму под действием сколь угодно малых сил, но для изменения самого объема жидкости или газа необходимы конечные силы, т. е. жидкость и газ ведут себя как упругие тела. Изменение формы, не связанное с изменением объема, идет в форме элементарных деформаций сдвига, но при быстрых деформациях сдвига в жидкости или газе могут возникнуть силы, которые зависят не от величины деформации, а от скорости деформации, т.е. при скорости деформации стремящейся к нулю, силы деформации также стремятся к нулю, а при больших скоростях мы имеем конечное значение этих сил. Данные силы надо рассматривать не как упругие, а как силы внутреннего трения, которые называются силами вязкости. Степень сжатия жидкости или газа определяет величину тех сил, с которыми одни части жидкости или газа действуют друг на друга или на соприкасающееся с ними тело. Если на некоторую площадку ∆S мы будем действовать силой ∆F, то: при ∆S→0: 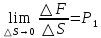 – внешнее давление жидкости или газа, по сути, являющееся нормальным напряжением. – внешнее давление жидкости или газа, по сути, являющееся нормальным напряжением.Все точки жидкости, лежащие в одной горизонтальной плоскости, находятся под одним давлением, которое на данной глубине распространяется во всех направлениях. Кроме того, в каждой точке жидкости существует давление, обусловленное собственным весом столба жидкости: ρgh = P2 и P1+P2= const=Pст – гидростатическое давление; P1+P2=Pст – основное уравнение гидростатики. Pст обусловлено потенциальной энергией жидкости, находящейся под давлением. Распределение давления по высоте объясняет возникновение подъемной силы, которая действует на тело, погруженное в жидкость или газ. Величина подъемной силы равна по величине и обратна по направлению объему V вытесненной жидкости или газа. Эта сила – называется силой Архимеда: Pn=ρgѴ - закон Архимеда. Линия действия силы Архимеда проходит через центр тяжести погруженного тела. Движение жидкости под действием перепада давления, силы тяжести, инерции и других сил можно описывать уравнениями Лагранжа или уравнениями Эйлера. Пространство, заполненное частицами движущейся жидкости и ограниченное системой поверхностей, называется потоком. Линия, касательная к направлению вектора скорости частицы жидкости в каждой точке потока и в каждый момент времени, называется линией тока. Путь, проходимый частицей жидкости в пространстве за определенный промежуток времени, называется траекторией. В установившихся течениях, линии тока совпадают с траекториями движущихся частиц жидкости. Поверхность, образованная линиями тока, называется трубка тока. Объемный пучок линии тока, - называется струйка тока. Малая площадка ∆S, представляющая собой поперечное течение струйки тока и перпендикулярная к линиям тока называется живым сечением линии тока. Уравнение Бернулли.
Рассмотрим связь между скоростью в стационарном потоке невязкой и несжимаемой жидкости. Изменение энергии рассматриваемого элемента жидкости должно быть равно работе внешних сил: Ui = ρ∙Si∙vi∙∆t∙g∙hi –потенциальная энергия элемента жидкости. Ti = 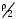 ∙Si∙vi∙∆t∙g∙ ∙Si∙vi∙∆t∙g∙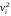 – кинетическая энергия элемента жидкости, тогда – кинетическая энергия элемента жидкости, тогда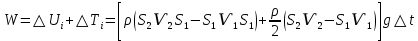 . .W = ΔUi+ ΔTi = [ρ(S2∙v2 h2 – S1∙v1 h1) + 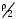 (∙S2∙ (∙S2∙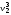 - ∙S1 - ∙S1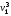 )] g ∆t )] g ∆tВнешние силы давления, действующие на наш объем через сечение 1 совершают положительную работу А и действуют в сторону перемещающейся жидкости. Силы, действующие через сечение 2, совершают отрицательную работу -А. Разница работ: 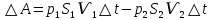 , ,а, по закону сохранения, изменение энергии равно работе, действующей на систему сил:  ∆W=∆A, значит мы можем записать: 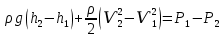 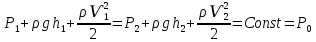 - уравнение Бернулли. - уравнение Бернулли.P+Pст+Pдин=P0, P0 – полное давление. Данное уравнение получено с учетом несжимаемости жидкости на основе закона сохранения энергии. Рассмотрим идеализированную модель движения жидкости из сосуда, внизу которого находится отверстие для истечения жидкости. 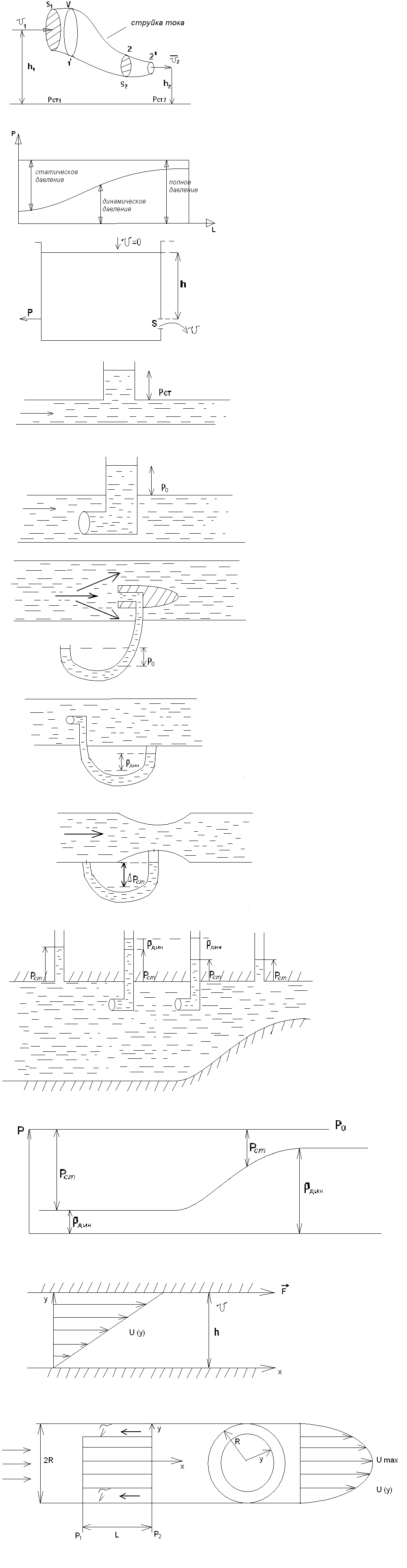 S – площадь выходного отверстия. Применим закон сохранения импульса. Имеем сосуд с жидкостью, поверхность которой имеет скорость Ѵ=0. На дне сосуда имеем отверстие площадью S, находящееся на глубине h от поверхности жидкости. Из данного отверстия вытекает струя жидкости, которая создает импульсы P. К движущейся жидкости применим закон сохранения импульса. 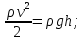 v= v=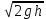 откуда: P=mv =2 откуда: P=mv =2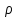 Sgh, Sgh,По закону Ньютона результирующая сила давления жидкости на стенку равна этой же величине, но направлена в противоположную сторону. В отличие от идеальных, скорость истечения реальных жидкостей имеет меньшее значение, особенно это заметно на непрофилированных отверстиях имеющих низкое качество. Вводится коэффициент корреляции, учитывающий качество отверстия – «коэффициент истечения». Измерение давления в потоках. Статическое давление в потоке измеряется путем перфорации стенки трубопровода и присоединения измерительной трубки, в которой происходит подъем жидкости на высоту h.  Полное давление измеряется с помощью трубки Пито, открытый конец которой направлен на встречу потоку.  Технически трубки Пито оформляются аэродинамически более совершенно. На трубку ставят аэродинамический обтекатель, обеспечивающий минимальное возмущение потока.   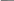  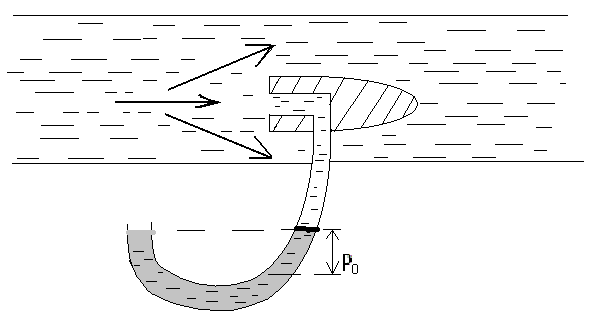 Разность между полным давлением и давлением статическим измеряют трубкой Прандтля:   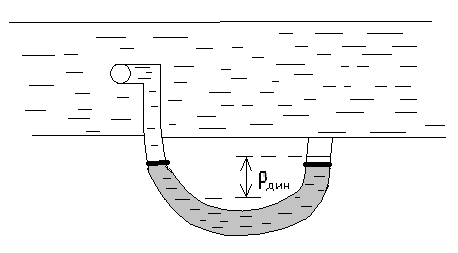 Разность двух статических давлений измеряют трубкой Вентури: 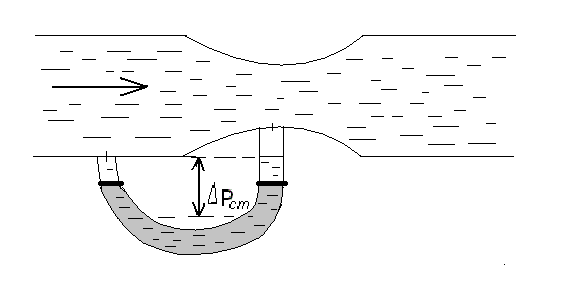 Рассмотрим движение жидкости в трубопроводе сложного профиля.  При движении в канале сложной формы изменения давления описываются формулой Бернулли, а приборы подтверждают это. Движение жидкости с учетом сил вязкости. При установившемся движении реальной жидкости или газа запас энергии в единицу массы не может оставаться постоянным, как при движении идеальной жидкости. Дело в том, что при движении реальной жидкости возникают силы внутреннего трения вследствие её вязкости, и возникает сопротивление движению, на преодоление которого затрачивается часть энергии. Прилегающий к стенке трубопровода слой жидкости практически не движется, он как бы прилипает к стенке. Внутренние слои жидкости движутся с постоянно увеличивающейся скоростью по мере удаления от стенки, т. е. наличие тангенсально направленных сил сопротивления приводит к тому, что прилипающий к стенке слой жидкости действует на соседний и на все другие слои. Обозначив потери вследствие трения как hТр мы будем иметь уравнение Бернулли для реальной жидкости в виде: P1+ρgh1+ρ 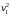 /2 = P2+ρgh2+ρ /2 = P2+ρgh2+ρ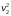 /2+hТр. /2+hТр.Т. е. запас энергии единицы массы жидкости уменьшается по направлению движения. Для выяснения распределения скорости между слоями жидкости и возникающие при этом силы рассмотрим задачи ламинарного течения (безвихревое, т. е. послойное течение вязких жидкостей, не сопровождающиеся турболизацией потоков и образованием вихрей) жидкости. Рассмотрим ламинарное течение жидкости, течение Куэтта или течение чистого сдвига.  Имеем две пластины, между которыми находится жидкость. К одной из пластин приложили силу F, вследствие чего пластина будет двигаться относительно неподвижной со скоростью v, и в этом случае при наличии между пластинами вязкой жидкости, у нас в жидкости образуется линейный профиль скорости U(y) (скорость зависит линейно от расстояния до подвижной стенки). Это называется течением Куэтта. Опыт подсказывает, что скорость в каждой точке:  При этом возникают касательные напряжения: 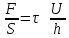 ; ;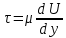 - закон трения Ньютона. - закон трения Ньютона.При линейной зависимости между напряжением (τ) и скоростями деформации - 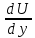 – жидкости называются Ньютоновские. – жидкости называются Ньютоновские.μ - коэффициент динамической вязкости; 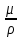 – коэффициент кинематической вязкости жидкости. – коэффициент кинематической вязкости жидкости.Большинство окружающих нас жидкостей имеют связь между тензором напряжений (τ) и тензором скоростей линейную, и это основная масса жидкостей – Ньютоновские. Существуют жидкости, в которых связь между этими тензорами нелинейная. Имеются вязкопластичные жидкости, в которых существует предельное напряжение сдвига, при превышении которого возникает текучесть жидкости. Это глинистые резервуары, грязи, масляные краски. Дилатантные жидкости – жидкости у которых внутреннее течение (вязкость) увеличивается с ростом скорости. Течение Хагена-Пуазейля. Течение Хагена – Пуазейля - это ламинарное, стационарное течение вязкой жидкости в трубе. (Ламинарное – послойное) Рассматривается течение в цилиндрической трубе диаметром Д=2R=Const. Движение жидкости осуществляется вдоль оси трубы под действием перепада давления. Параметры жидкости в поперечном сечении трубы постоянны. Жидкость у стенок трубы прилипает к ней, и вследствие сил вязкости влияние прилипшего слоя жидкости передается от стенки к оси трубы, что приводит к изменению скорости течения жидкости. Т. о. => перепад давления ускоряет жидкость, а силы трения ее тормозят. Рассмотрим цилиндрический элемент жидкости.  Уравнение движения для цилиндрического слоя жидкости имеет вид: (Р1-Р2) πу2=2πуLτ Отсюда: 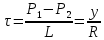 И по закону Ньютона: 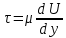 => можем записать: => можем записать: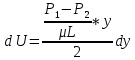 проинтегрировать это выражение: 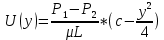 Константа интегрирования С получается из граничных условий: Y=R; U(y)=0 => C=R2/4 Получим: 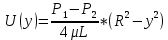 т. е. при движении вязкой жидкости в ламинарном режиме течения в цилиндрической трубке, мы имеем параболическое распределение скорости, при этом максимальная скорость достигается на оси трубы и равняется: 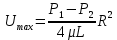 Найдем расход жидкости, двигающейся по трубе. Из геометрии следует, что объем параболоида вращения равен произведению 1/2 высоты на площадь основания, т. е.: 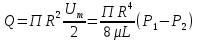 - закон Хагена – Пуазейля. - закон Хагена – Пуазейля.Гидравлические сопротивления и виды потерь напора. В широком смысле трубопроводы можно представить в качестве моделей как автомагистрали для движения газов, жидкостей, суспензий и другого. Трубопроводы имеют самую разную форму и протяженность, следовательно, разделяются на простые и сложные. Простые не имеют ответвлений, среда в них движется с постоянным расходом на всех участках. Сложные имеют различные отводы, параллельные участки, шунтирующие элементы и поэтому относящиеся к сложным. При движении жидкости по трубопроводу происходят затраты энергии потока на преодоление сопротивления движению, т. е. происходят потери напора. В общем случае из уравнения Бернулли для потока реальной жидкости имеем: 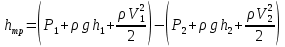 Возникающие при движении жидкости сопротивления можно разделить на: сопротивление по длине потока местное сопротивление Первые проявляются по всей длине трубы и пропорциональны длинам участков, они обусловлены силой трения, возникающей в жидкости. Местные сопротивления обусловлены различными конструкционными особенностями, геометрией элементов, местными преградами в потоке (поворот, колено, отвод, крестовина, сужение, кран и т. д.) Соответственно этому потери напора бывают: а) по длине б) местные Существуют принципы наложения потерь по длине и местных, тогда: 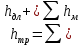 при этом надо учитывать, что существует взаимное влияние(интерференция) местных сопротивлений, расположенных близко в потоке. И в связи с этим в некоторых случаях суммарная потеря напора не равна простой сумме потерь напора из-за взаимного влияния. Потери отражаются формулой Вейсбаха: 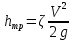 где 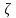 - коэффициент потерь, показывающий долю скоростного напора, затраченного на преодоление данного сопротивления; 𝒱 – средняя скорость потока. - коэффициент потерь, показывающий долю скоростного напора, затраченного на преодоление данного сопротивления; 𝒱 – средняя скорость потока.Существуют: 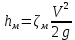 ; ; 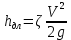 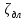 определяется формулой Дарси: определяется формулой Дарси: 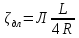 , где , гдеЛ – коэффициент сопротивления трению по длине; R – гидравлический радиус трубы 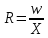 , W – живое сечение трубы, , W – живое сечение трубы, 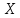 - смоченный периметр трубы. - смоченный периметр трубы.Если труба круглая, то: 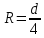 Окончательно потери напора по длине трубы: 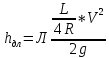 – для всех типов труб – для всех типов труб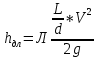 – для круглых труб – для круглых труб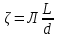 (для круглых труб) (для круглых труб)Эти формулы для круглых и другого типа труб – формулы Дарси –Вейсбаха. |