ОТВЕТЫ. Блок а раздел 1 Основы гидростатики 1 Основные понятия и определения
 Скачать 1.68 Mb. Скачать 1.68 Mb.
|
|
Тема 6: Ударная адиабата (адиабата Ренкина-Гюгонио). Выпишем уравнения сохранения массы, импульса и энергии для стационарного течения элементарной струйки, площадью 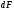 , проходящая через сильный разрыв: , проходящая через сильный разрыв: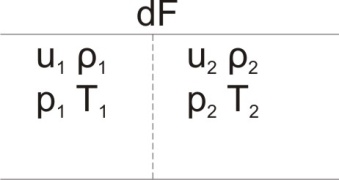 Для определения неизвестных за скачком уплотнения, запишем сохранения:  ρ1∙U1=ρ2∙U2 – уравнение неразрывности (сохранение массы) ρ1∙U1=ρ2∙U2 – уравнение неразрывности (сохранение массы)ρ1∙U12+P1=ρ2∙U22+P2 – сохранение импульса (8) CpT1+ 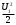 =CpT2+ =CpT2+ 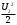 =h0=CpT0 – сохранение энергии =h0=CpT0 – сохранение энергииДобавим уравнение состояния: P2=ρ2∙R∙T2 Здесь индексом 1 отмечены параметры невозмущенного потока (т.е. до скачка), а 2 – за скачком. 0 – параметры торможения. Используя (8) для газа с постоянными теплоемкостями и выражение для внутренней энергии ε= 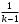 ∙ ∙ 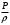 , мы можем получить связь параметров состояния газа на ударной волне: , мы можем получить связь параметров состояния газа на ударной волне:[ε]+ 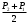 ∙[ ∙[ 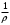 ]=0 (9) – уравнение адиабаты для идеального газа. ]=0 (9) – уравнение адиабаты для идеального газа.После преобразования в (9), получим: 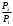 = = 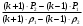 ( (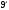 ) – уравнение адиабаты в виде Ренкена – Гюгонио. ) – уравнение адиабаты в виде Ренкена – Гюгонио.Уравнение ( 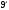 ) можно преобразовать, получим: ) можно преобразовать, получим: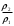 = = 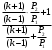 ( (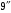 ) )Из этих выражений можно сделать выводы: Пусть скачок давления на ударной волне очень большой, тогда предел изменения плотности воздуха будет стремиться к 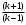 и для плотности воздуха стремится к 6. Но, если и для плотности воздуха стремится к 6. Но, если 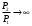 , а , а 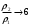 , то из уравнения состояния: , то из уравнения состояния: 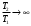 ,т.е газ в ударных волнах может достигать очень высоких температур. Анализ скорости распространения поверхности сильного разрыва относительно движущихся частиц газа θ с учетом (9) позволяет сказать, что скорость распространения ударной волны сверхзвуковая с одной стороны волны, и дозвуковая с другой. ,т.е газ в ударных волнах может достигать очень высоких температур. Анализ скорости распространения поверхности сильного разрыва относительно движущихся частиц газа θ с учетом (9) позволяет сказать, что скорость распространения ударной волны сверхзвуковая с одной стороны волны, и дозвуковая с другой.Т.е. ударные волны в стационарных течениях могут существовать лишь тогда, когда течение хотя бы с одной стороны ударной волны сверхзвуковое. Анализируя систему (8) и используя выражение ( 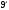 ), можно получить связь параметров на ударной волне. ), можно получить связь параметров на ударной волне.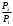 = = М12 - М12 - 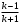 (10), откуда следует, что при М1=1 P2=P1, т.е. нет разрыва при М1 (10), откуда следует, что при М1=1 P2=P1, т.е. нет разрыва при М1 1. 1.Подставляя в выражение (10) выражение ( 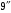 ), получим: ), получим: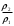 =λ12 (11), откуда видно, что наибольшее значение отношения плотностей происходит при λ1 стремящемуся к максимуму, т.е. при =λ12 (11), откуда видно, что наибольшее значение отношения плотностей происходит при λ1 стремящемуся к максимуму, т.е. при 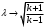 . .Рассматривая систему уравнений динамической совместимости для плоского стационарного течения мы видим, что скорость распространения ударной волны θ=N-Un, а т.к. течение стационарное, то N=0, тогда уравнение энергии: ρ∙θ∙[ 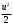 +ε]= - [ρ∙θ∙ +ε]= - [ρ∙θ∙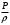 ], или ρ∙θ∙ ], или ρ∙θ∙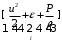 =0, следовательно ρ∙θ∙i0=0, т.е. i0=0. =0, следовательно ρ∙θ∙i0=0, т.е. i0=0.Т.е. полное теплосодержание при переходе через ударную волну остается без изменения. Тема 7: Косые скачки уплотнения. В прикладных задачах газодинамики появление прямых изолированных скачков уплотнения весьма редко. Обычно, при движении тел со сверхзвуковыми скоростями, или при движении сверхзвукового потока в каналах, трактах, соплах, возникают сложные системы скачков уплотнения, содержащих участки как прямых, так и косых скачков уплотнения. 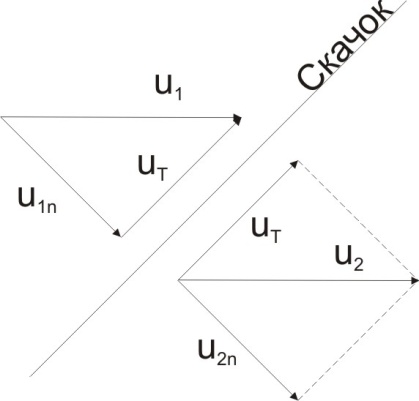 Если на сверхзвуковой поток, в котором имеется прямой скачок уплотнения наложить течение с дозвуковой или сверхзвуковой скоростью Uτ, направленной перпендикулярно скорости исходного сверхзвукового потока U1n, то возникшее суммарное течение будет являться потоком с косым скачком уплотнения. В связи с отсутствием каких-либо сил в направлении Uτ, данная скорость не меняется при переходе через фронт ударной волны, а т.к. нормальная составляющая U2nменьше, чем U1n, то мы имеем, что U1>U2. Типичным примером возникновения косого скачка является обтекание клина сверхзвуковым потоком газа. 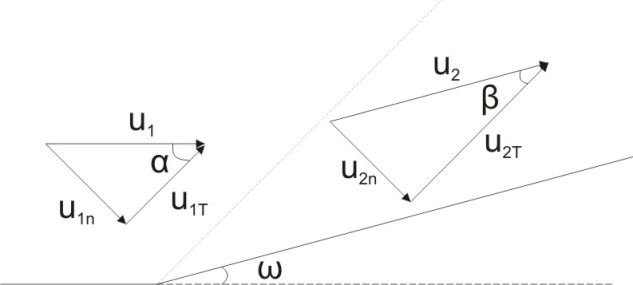 При этом вектор скорости перед скачком - U1 – параллелен одной стороне клина, а вектор скорости после скачка - U2 – параллелен другой стороне клина. Угол между скоростью набегающего потока и фронтом косого скачка уплотнения обозначим α. А угол между вектором скорости после скачка и его фронтом – β. Т.к. нормальная составляющая скорости при переходе через скачок уменьшается, а величина вектора Uτ не меняется, то вектор скорости U2 “прижимается” к фронту скачка, т.е. всегда β<α и поворот вектора скорости в косом скачке уплотнения: ω=α-β и он совпадает с углом наклона обтекаемого потоком клина. Для нормального к фронту косого скачка уплотнения составляющей скорости Un выполняются законы сохранения массы и импульса; а в следствии того, что Uτ=const, то для нормальной составляющей скорости Un выполняется закон сохранения энергии. Ударная поляра. Для решения практических задач найдем связь параметров газа в зависимости от угла наклона ударной волны. Будем рассматривать поток, в котором находится ударная волна. 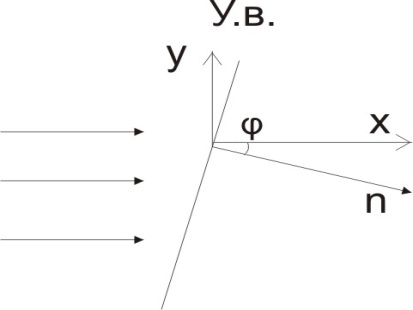 Ось x взята вдоль скорости набегающего потока до ударной волны. Ищется связь между проекциями Uy и Uxпри известных параметрах набегающего потока ударной волны: Uy=f (Ux ,U1 , C1). Пропуская выкладки имеем следующий вид связи параметров: Uy2=(Ux - U1)2 ∙ 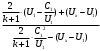 . . Данное уравнение называется ударной полярой. Ударная поляра – кривая, представляющая собой геометрическое место точек конца радиус-вектора скорости за ударной волной, различной интенсивности и формы при известных параметрах газа до ударной волны. Геометрически эта фигура называется гипоциссоидой или декартовым листом. У 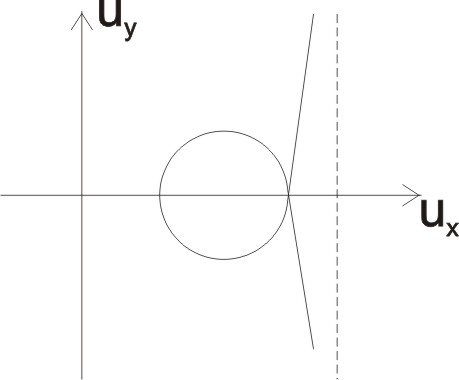 ходящие на асимптотику ветви ударной поляры физического смысла не имеют. ходящие на асимптотику ветви ударной поляры физического смысла не имеют. Изменение давления в косой ударной волне описывается формулой: 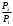 = = 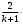 М12∙ М12∙ 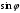 - - 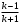 . .Турбулентное течение несжимаемой жидкости. Неустойчивость международных режимов течений возникновение турбулентности. Ламинарные, или сложные, течение – это течение траектории частиц в которой линии тока, поля скоростей и давлений имеют «регулярный» характер. Они хорошо описываются решениями уравнений. Навье-Стокса при регулярных граничных и начальных условий. Например, Пуазейлево течение, теория смазки и д.р. Наличие в реальных условиях чаще всего малых по величине случайных возмущений параметров тока может либо очень слабо изменить рассматриваемое движение (это говорит об устойчивости движения по отношению к малым возмущениям) либо полностью его исказить (это говорит о неустойчивости движения). Т.е. в деятельности наблюдаются только такие течения, решения уравнений Навье – Стокса, которые их описывают являются устойчивыми. В случае неустойчивого движения малые возмущения не затухают, а растут, и могут перевести течение в новое устойчивое состояния, если таковое имеется среди возможных решений уравнений Навье – Стокса, либо к хаотичному с нерегулярно движущимися и взаимодействующими между жидкими массами. Эта форма жидкости широко распространена в природе и носит название турбулентное движение жидкости. Примером является колышущиеся злаковые поля, вода в канаве, клубы дыма и др. С увеличением скорости движения потока ламинарное течение терпит устойчивость, случайные возмущения, которые раньше вызывали лишь колебания струек вокруг устойчивого их прямолинейного движения быстро развиваются и приводят к новой турбулентной форме течения жидкости. Существует критическое число Ренольдса Re 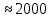 и в этом случае, если Re и в этом случае, если Re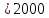 , то любые возмущения, имеющиеся в движущихся жидкостях затухают. , то любые возмущения, имеющиеся в движущихся жидкостях затухают.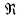 min= min=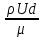 И существует верхнее критическое число Re верхнее Remax=5*105 Кроме того мы, например имеем конфузор, цилиндр, диффузор.       Reкрконф > Reкр цил > Reкрдиф Шероховатость стенок не влияет на число Reкр нижнее, т.к. нижнее число Рейнольдса связано с устойчивостью потока, а не с наличием в нем возмущений. А на верхнее критическое число Рейнольдса шероховатость оказывает влияние, т.к. поток уже неустойчив и его надо подтолкнуть. Ламинарное течение переходит в турбулентное и в нем возникают поперечные движения масс жидкости переменивая обмен импульсов в направлении перпендикулярном движению. Происходят перераспределение скоростей по поперечному течению трубы. При этом распределение профиля скоростей становятся более равномерным.              Umax Umax   U(y) U(y)      В полях скоростей и давлений в каждой точке пространства имеются, пульсации параметров и это влияет на сопротивления; для турбулентных течений сопротивления становятся пропорциональным квадрату скорости. Крылья (птиц) с затянутым ламинарным пограничным слоем обладают малым сопротивлением, но легко теряют свое преимущество при дожде, при попадании насекомых, пыли и других параметров, обеспечивающих возмущение потока. С другой стороны опушенность перьев птиц создает сложные воздушные вихри, которые подменяют трение воздуха о крыло трением внешнего потока о слой вихрей. Получается подъемная сила. Крыло описывает сложную кривую и даже при взмахе вверх существует подъемная сила и тяга вверх. Крыло работает одновременно как винт и как крыло самолета, при этом у птиц легко меняется и профиль крыла. Различные перья работают для быстрого или медленного полета. Существует развитая ламинарная теория устойчивых ламинарных течений, развивается нелинейная теория. Методом теорий колебаний изучается поведение возмущений конечной амплитуды. При Re близких к Re критическим, происходит чередование ламинарных и турбулентных режимов течении. Этот процесс характеризуется перемещаемость ɣ. Мерой ɣ является доля времени существование турбулентного режима в данной точке потока, т.е. ɣ= ɣ(Re, x), поэтому переход от ламинарного течения к турбулентному проходит через “облака”, “пятна” а в трубах через “пробки”. Т.е. при ɣ=0 мы имеем чисто ламинарное течение, а при ɣ=1 чисто турбулентное. Рассмотрим переход от ламинарного режима течения, к турбулентному в трубе:     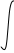  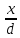 9500 95001 _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _    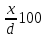 0,5       2000 3000 Re 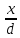 –расстояние то входа в трубу к диаметру. –расстояние то входа в трубу к диаметру. 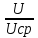 Профиль скорости при турбулентном потоке в трубе. 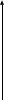 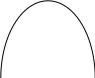  ɣ=0 2 __ _ _ _ _   ɣ=1 1 _          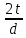 -1 1 0 0  Рассмотрим переход ламинарного течения в турбулентное. Рассмотрим переход ламинарного течения в турбулентное.   4 2                     1 3 2 Re 4000 3000 2000 1000 1 1) скорость переднего фронта турбулентной пробки 2) скорость заднего фронта турбулентной пробки 3) скорость на оси трубы при турбулентном течении 4) скорость при ламинарном течении Чему равно гидростатическое давление в точке А? 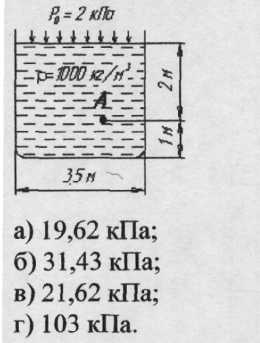 |
