ОТВЕТЫ. Блок а раздел 1 Основы гидростатики 1 Основные понятия и определения
 Скачать 1.68 Mb. Скачать 1.68 Mb.
|
|
Сжимаемость. Сжимаемостью называется способность жидкости или газа изменить свой объем под действием сил внешнего давления. Мерой сжимаемости является модуль объемной упругости Е. который меняет смысл напряжения, при котором относительные изменения объема равны единице. Для газов при невысоком изменении объема, которое происходит при постоянной температуре, модуль объемной упругости равен Р0: 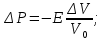 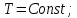 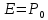 (P0+∆P) (V0+∆V)= P0 V0 ; PV=RT= P0 V0= Const Раскрывая скобки и отбрасывая величины малого порядка, получим: 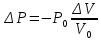 откуда видно, что E=P0. Сжимаемость необходимо учитывать, когда изменение давления, вызванное движением газа, оказывает существенное влияние на объем. Рассмотрим изменение плотности: (ρ0+∆ρ) (V0+∆V)=ρ0 V0 ; 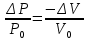 ; ;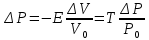 , откуда следует: , откуда следует:Запишем уравнение Бернулли в общем виде: 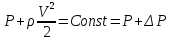 , где Р – статическая составляющая, ∆Р динамическая составляющая. , где Р – статическая составляющая, ∆Р динамическая составляющая.Рассмотрим статическую составляющую: 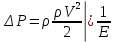 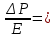 Используем уравнение Лапласа: 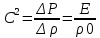 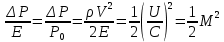 ↗ связь P, E, 𝒱. С – скорость распространения малых возмущений – звук. Модели движения газожидкостной среды. При движении вязкой жидкости, при обтекании тел и поверхностей проявляется влияние обусловленное вязкими свойствами среды. Рассматривая течение только Ньютоновской жидкости имеем неоднозначное влияние вязкости на характер течения. В некоторых задачах вязкость играет решающую роль, в других влияние чрезвычайно слабое и пренебрежение вязкими силами облегчает исследование и в этом случае вместо реальной жидкости мы можем рассматривать течение жидкости идеальной. Идеальная жидкость – это абстрактная жидкость, лишенная внутренних сил трения. При нарушении равновесия, под действием сил, частицы жидкости приобретают ускорение. Скорость частицы зависит от времени и пространственных координат. Точно так же от них зависит и давление. υ = υ(x,y,z,t) P=P(x,y,z,t) Такое движение – неустановившееся, но если параметры потока не меняются с течением времени, то υ = υ(x,y,z) P=P(x,y,z) Как термодинамическая система жидкость может характеризоваться параметрами, которые подразделяются на экстенсивные(величина не зависит от объема системы – V, U, S) и интенсивные(P, T, ρ). Температура – величина характеризующая степень нагретости тела и связана с мерой средней кинетической энергии поступательного движения молекул газа. Кинематика жидкой частицы Рассмотрим кинематику жидкой частицы. Кинематика жидкости изучает жидкость в движении, не рассматривая сил, порождавших или сопровождавших это движение. В кинематике используется сплошная модель жидкости: некоторый ее континуум. Согласно гипотезе сплошности, рассматриваемый континуум – это жидкая частица, в которой беспрерывно движется огромное количество молекул; в ней нет ни разрывов, ни пустот. Существует два метода изучения движения жидкости: Метод Лагранжа рассматривает движение каждой индивидуальной частицы. Вводится понятие траектории. Движение одной частицы жидкости можно задать системой трех уравнений: Для задания движения всех частиц потока жидкости потребовалось бы бесконечное множество таких уравнений. Каждая частица жидкости в начальный момент времени находится в определенной точке пространства, определяемого начальными координатами . Выбирая начальные координаты, тем самым мы выбираем в потоке жидкости определенную частицу. Текущие координаты этой частицы будут другими, чем текущие координаты частицы с другими начальными координатами. Таким образом, считая начальные координаты переменными, движение потока жидкости может быть задан следующей системой уравнений: Текущие координаты произвольной частицы жидкости в потоке есть функции четырех переменных: Скорости и ускорения частиц жидкости при движения способом Лагранжа определятся следующим образом: 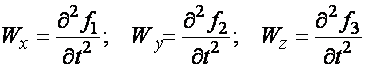 При исследовании движения способом Лагранжа геометрическими характеристиками движения потока жидкости будут траектории и линии отмеченных. Траектории движения частиц жидкости можно получить, исключив время системы уравнений (1). Метод Эйлера изучает поля векторных или скалярных величин, оставляя в стороне вопрос о том, как движется каждая индивидуальная частица. Здесь вводится понятие местной скорости или скорости в точке. Рассмотрим движение частиц в некоторой области. В каждой точке этой области в заданный момент времени частицы жидкости имеют скорости. Вся совокупность векторов, изображает определенные скорости, составляет так называемое векторное поле скоростей (см. Рисунок). Координаты точки зафиксированы, то есть со временем не меняются. Так же координаты других точек пространства не меняются. Если движение жидкости устойчивое, т.е. не меняется по времени, то вектора скоростей частиц жидкости, проходящих через фиксированные точки пространства, меняться не будут. Иными словами, в разные моменты времени через фиксированные точки пространства протекать различные частицы жидкости, но вектора скоростей их в каждой фиксированной точке пространства будут одинаковыми. Картина поля скоростей при установившемся движении не меняется по времени.  Тогда, если задать следующие функции: то говорят, что задано векторное поле скоростей. По заданному векторному полю скоростей можно определить все кинематические и геометрические характеристики потока жидкости. Если движение жидкости неустановившийся, то в каждый момент времени скорости частиц жидкости, проходящих через фиксированные точки пространства, будут различными. Поэтому, чтобы задать векторное поле скоростей при неустановившемся движении, необходимы другие уравнения: Уравнение (2) и (3) является уравнение, с помощью которых задается движение жидкости при установившемся и неустановившемся движениях. Такой способ задания движения жидкости называется способом Эйлера. Поскольку при установившемся движении скорости частиц жидкости, проходящих через фиксированные точки пространства, не зависят от времени, аналитические условия устойчивого движения могут быть выражены: формулу для определения ускорений частиц жидкости при задании движения способом Эйлера. Составим выражения полных производных по времени от проекций скоростей, учитывая, что полный дифференциал равно сумме частных дифференциалов Разделим обе части уравнений (5) на и введем следующие ограничения: где - углы между дифференциалом перемещение частицы жидкости и осями координат, то есть - проекции элементарного перемещения частицы на оси координат. Тогда: Уравнение (2.6) можно кратко записать в векторной форме, если ввести дифференциальный оператор: Тогда: Теорема Коши – Гельмгольца: скорость любой жидкой частицы складывается из скорости полюса, скорости вращения вокруг мгновенной оси, проходящей через этот полюс, а также скорости деформационного движения, состоящего из линейной деформации и деформации сдвига. Тема 2: Термодинамические параметры газа. Состояние и физические свойства газа характеризуются его температурой Т, давлением Р, плотностью ρ, внутренней энергией ε. Температура газа в аэродинамике обычно измеряется в абсолютной шкале Кельвина, однако, в связи с тем, что многие приборы градуируются по шкале Цельсия, в некоторых записях и формулах используют и ее. В дальнейшем будем употреблять значение для температуры по шкале Цельсия и записывать t0C, для Кельвина – Т. Между ними существует связь: Т=t+273,15. Давление, которое, по сути, является нормальным напряжением, есть отношение нормальной силы, действующей на элемент площадки, к величине площадки, при величине площадки, стремящейся к нулю: Р= 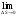 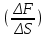 существует большое количество единиц измерения давления. В СИ за единицу давления принят Паскаль. Паскаль – давление, вызываемое силой в 1Н, равномерно распределенной на поверхности в 1м2. Кроме этого, для измерения давления в аэродинамике используются такие единицы: 1 атмосфера – давление 1кг силы на 1см2. Различают техническую и физическую атмосферы. Техническая: 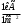 . Физическая: 9,80665∙104 . Физическая: 9,80665∙104 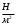 (Па) (Па)1 мм рт. ст. Эта единица применяется для измерения давлений в барометрах, жидкостных манометрах и т.д.1 мм рт. ст. =133,322 Па. 1 мм.в.ст=9,80665 Па. Таким образом, вода и ртуть различаются в 13 раз. Большие перепады давлений измеряются ртутными манометрами, малые – микроманометрами с водно-спиртовым раствором. Нормальное давление: 760 мм.рт.ст=1,013∙105 Па=10,333 мм вод.ст. Плотность – масса вещества, распределенная в единице объема. В СИ: 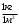 На практике часто пользуются понятием “удельный вес газа (жидкости)” в единице объема, он обозначается: γ, [ 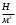 ]. ].Внутренняя энергия ε характеризует энергию теплового движения единицы массы газа. СИ: ε= 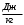 . . Энергетическое состояние газа определяется энергиями входящих в него молекул. Молекулы имеют поступательную, вращательную и колебательную составляющие энергии. Кроме этого, колебательными и вращательными составляющими энергии обладают атомы и электроны, составляющие молекулу. Все это является внутренней энергией газа ε. Обычно внутренняя энергия единицы массы газа определяется так: ε=ε(P,T). Это уравнение называют калорическим уравнением состояния. Термодинамические уравнения состояния. Термодинамические параметры газа связаны между собой уравнением состояния. Для давлений до 1000 атм. С большой степенью точности состояния газа подчиняются следующему уравнению состояния: P=ρRT, где R – газовая постоянная. Это уравнение состояния для точки газа, которая состоит из большого количества молекул, но которая является малой в рассмотренном потоке. Газ, параметры которого подчиняются данному уравнению, называют совершенным (идеальным). Внутренняя энергия характеризует энергию теплового движения молекул. При давлениях больше 1000 атм. следует пользоваться уравнением Ван-дер-Ваальса: (Р+ 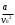 )(v0-b)=RT, где: )(v0-b)=RT, где: 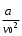 - поправка, учитывающая взаимное притяжение молекул; b – учитывает объем, занимаемый молекулами газа. - поправка, учитывающая взаимное притяжение молекул; b – учитывает объем, занимаемый молекулами газа.Тема 3: Законы сохранения и адиабатическое течение. Рассмотрим установившееся (стационарное) квазиодномерное течение в каналах, соплах, трубах, струйках и запишем описывающие эти течения законы сохранения. 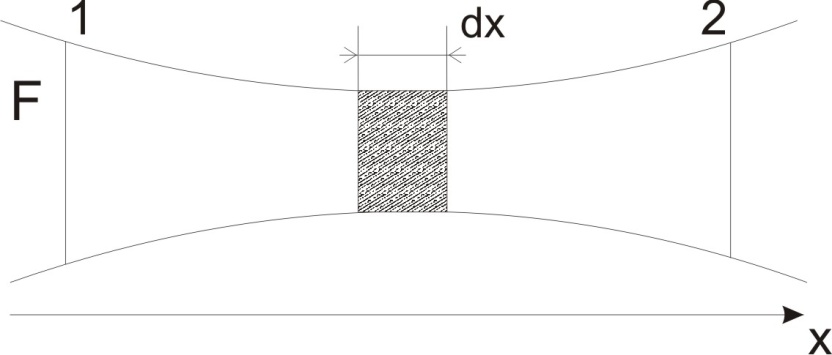 Введем координату x вдоль потока и площадь F поперечного сечения, нормального к координате x. Тогда законы сохранения: 1. G=ρuF (1) – закон сохранения массы (уравнение неразрывности), которое гласит: сколько массы прошло через сечение 1, столько же прошло через сечение 2. 2. ρu 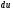 + +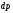 =0 (2) – закон сохранения импульса =0 (2) – закон сохранения импульсаДля несжимаемой жидкости уравнение (2) интегрируется и в результате получается уравнение Бернулли: ρ∙ 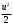 +pст=p0 (3), +pст=p0 (3),где ρu2/2 – динамическая составляющая полного давления, pст – статическая составляющая полного давления, p0 – полное давление (давление торможения). Графически (3) выглядит так: При изменении площади проходного сечения трубы для выполнения закона (3) мы должны иметь коррелированную связь между значениями статического и динамического давлений. p0 – давление заторможенного без энергетических потерь потока. Корреляция – взаимозависимость, взаимосвязь. Примером может служить емкость высотой h, из которой происходит истечение. 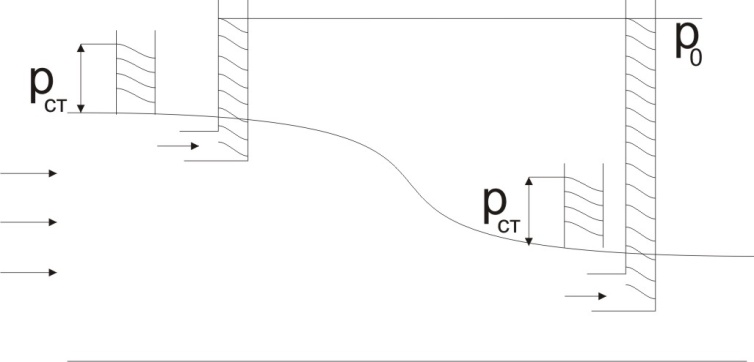 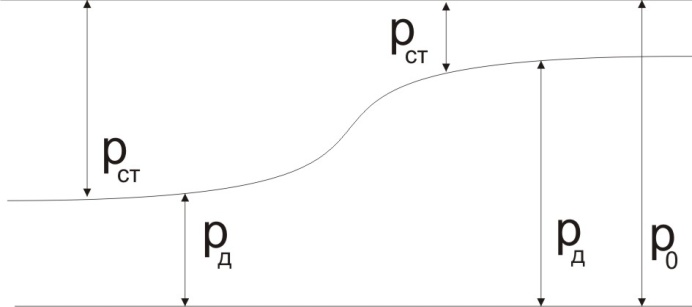 Тема 4: Звук. Звуковые волны. Конус возмущения. Колебательное движение с малыми амплитудами распространяется в среде в виде возмущений благодаря упругим свойствам данной среды, и называются звуковыми волнами. В каждом месте жидкости в звуковой волне происходи переменное сжатие и растяжение. Поверхность, отделяющую область, занятую возмущениями от невозмущенной среды называют фронтом волны. Она является поверхностью слабого разрыва, на которой терпят разрыв производные параметров состояния. Поверхность слабого разрыва распространяется в среде со скоростью, равной скорости звука. Пусть равновесные давление и плотность невозмущенной среды равны соответственно: Pрав, ρрав, а значения P! и ρ! – возмущения параметров. Тогда актуальные значения давления и плотности: 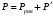 и и 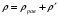 Графически это выглядит так: 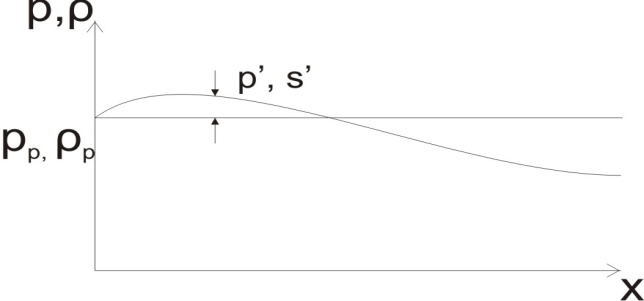 Т.е. имеем актуальное значение, равное равновесному, на которое накладываются пульсации параметра. Рассмотрим сферическую звуковую волну и два положения ее фронта в близкие моменты времени t1 и t2. 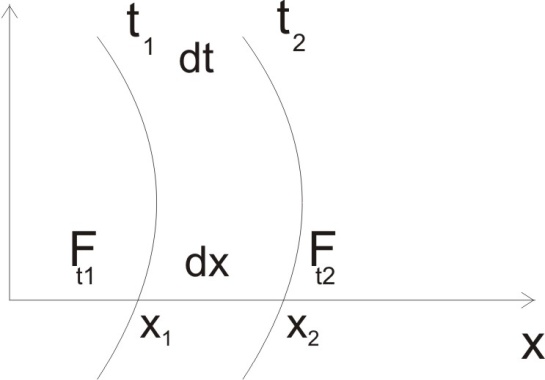 За промежуток времени 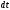 радиус фронта волны увеличился на радиус фронта волны увеличился на 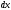 и тогда можно определить, что скорость распространения волны: a= и тогда можно определить, что скорость распространения волны: a= 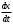 . .Через поверхность Ft1 в момент времени t1 под действием импульса возмущений 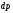 втекает масса жидкости со скоростью втекает масса жидкости со скоростью 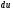 . Движение жидкости через поверхность Ft2 под действием перепада давления пока отсутствует. . Движение жидкости через поверхность Ft2 под действием перепада давления пока отсутствует.Изменение количества движения m 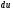 равно импульсу внешних сил, т.е.: m равно импульсу внешних сил, т.е.: m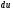 = =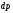 ∙ Ft1 ∙ ∙ Ft1 ∙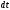 , а т.к. m=ρ∙ V, то втекла масса жидкости m=ρ∙V=ρ∙ Ft1 ∙ , а т.к. m=ρ∙ V, то втекла масса жидкости m=ρ∙V=ρ∙ Ft1 ∙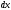 ; тогда ρ∙ Ft1∙ ; тогда ρ∙ Ft1∙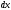 ∙ ∙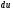 = =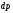 ∙ Ft1 ∙ ∙ Ft1 ∙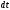 , откуда: , откуда: 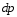 =ρ∙ =ρ∙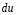 ∙ ∙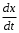 =ρ∙a∙ =ρ∙a∙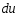 . .Для определения величины 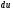 , идущую через поверхность, воспользуемся законом сохранения массы, т.е. рассмотрим ситуацию, когда волна зашла в промежуток между фронтами в положении x1 и x2, но масса газа не стала перетекать через поверхность Ft2. В данной ситуации у нас нет стока жидкости, следовательно, есть повышение давления на , идущую через поверхность, воспользуемся законом сохранения массы, т.е. рассмотрим ситуацию, когда волна зашла в промежуток между фронтами в положении x1 и x2, но масса газа не стала перетекать через поверхность Ft2. В данной ситуации у нас нет стока жидкости, следовательно, есть повышение давления на 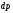 . .Масса, вошедшая вовнутрь двух фронтов волны:ρ∙ Ft1∙ 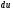 ∙ ∙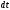 = Ft1∙ = Ft1∙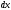 ∙ ∙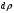 , или: , или: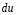 = =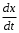 ∙ ∙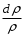 =a∙ =a∙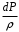 , откуда: a= , откуда: a=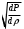 - скорость звука. - скорость звука.Для всех реальных сплошных сред при адиабатических процессах повышение давления вызывает рост плотности и величина 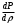 больше нуля. больше нуля.Т.к. звуковые волны совершаются адиабатически и являются малыми, они не могут быть причиной изменения энтропии. Поэтому в общем случае из энтропического движения: a2=( 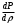 ) при S=const. ) при S=const.Используя уравнение состояния P=ρRT и уравнение адиабаты Пуассона 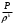 =const, для идеального газа получим: а= =const, для идеального газа получим: а=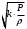 = =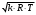 . .Движение газа имеет существенно различный характер в зависимости от того, является ли оно дозвуковым или сверхзвуковым. Принципиальным отличием между ними является возможность существования ударных волн в сверхзвуковых потоках. Если в каком-нибудь месте стационарно движущийся газ повергается слабому возмущению, то влияние этого возмущения распространяется по газу со скоростью, равной скорости звука относительно самого газа. Относительно неподвижной системы координат скорость складывается из двух частей: возмущение сносится потоком газа со скоростью потока 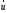 и распространяется относительно газа со скоростью звука а. и распространяется относительно газа со скоростью звука а.Рассмотрим однородный плоскопараллельный поток газа, движущийся со скоростью 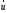 . Точечный источник возмущения движется в этом потоке также со скоростью . Точечный источник возмущения движется в этом потоке также со скоростью 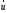 . Пусть в данный момент . Пусть в данный момент 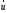 Источник все время сносится с газом и скорость распространения возмущений равна а 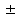 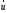 , т.е. мы имеем эксцентричность распространения звуковых волн. , т.е. мы имеем эксцентричность распространения звуковых волн.Выделим несколько положений тела в некоторые моменты времени. Относительно движущейся жидкости возмущения из точки А всегда будут распространяться сферическими окружностями. Скорость их распространения будет равняться  . Тело, непрерывно перемещаясь с жидкостью со скоростью . Тело, непрерывно перемещаясь с жидкостью со скоростью 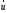 , непрерывно меняет координату источника возмущений А, поэтому в направлении вектора скорости по потоку скорость распространения возмущений будет равна , непрерывно меняет координату источника возмущений А, поэтому в направлении вектора скорости по потоку скорость распространения возмущений будет равна 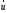 +a, а против потока +a, а против потока 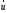 -a. В произвольном направлении скорость распространения возмущений определяется как сумма векторов -a. В произвольном направлении скорость распространения возмущений определяется как сумма векторов 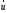 и а. и а.В итоге, при дозвуковых течениях возмущения распространяются по всему потоку, и взаимодействие потока с любым находящимся в нем телом идет с учетом его возмущающего действия на поток. Рассмотрим однородный плоскопараллельный поток газа, движущийся со скоростью 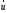 >a. >a.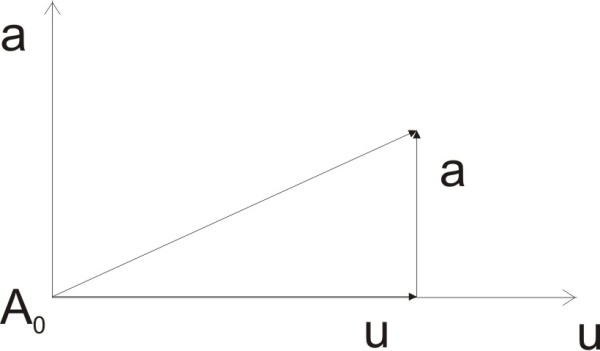 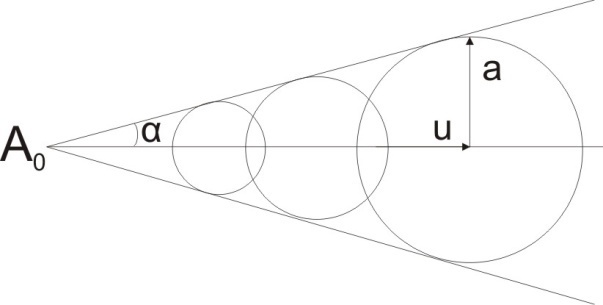 В сверхзвуковом потоке, где 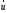 >a, возмущения могут лежать только внутри конуса с вершиной в точке А0, касающегося построенной из конца вектора >a, возмущения могут лежать только внутри конуса с вершиной в точке А0, касающегося построенной из конца вектора 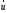 , как из центра сферы. Этот конус называется конусом Маха, угол α – угол Маха, а отношение М= , как из центра сферы. Этот конус называется конусом Маха, угол α – угол Маха, а отношение М=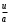 - число Маха. - число Маха.Т.е. в сверхзвуковом потоке возмущение, исходящее из какой-либо точки, распространяется вниз по потоку внутри конуса с углом α. Конус маха называют характеристической поверхностью, а линии, ее образующие – линиями Маха. В общем случае поверхность может не быть конической. Т.о., если в дозвуковом потоке наличие препятствия изменяет движение потока во всем пространстве, то сверхзвуковой поток натекает на препятствие “слепо”. Тема 5: Поверхности разрыва в газовой динамике. Ударные волны. Скачки уплотнения. При движении газа возможно существование поверхностей, которые зависят от координат и времени, и на которых происходит разрыв газодинамических параметров ρ, Р, U, Т. Они описываются в виде: 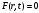 , где , где 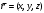 (1). (1). - радиус-вектор точки, где терпят разрыв сами параметры, описывающие состояние газа и эти поверхности называются поверхностями сильного разрыва. - радиус-вектор точки, где терпят разрыв сами параметры, описывающие состояние газа и эти поверхности называются поверхностями сильного разрыва.Если разрыв терпят только производные параметров, то поверхности называются поверхностями слабого разрыва. Разрыв обозначается так: 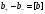 , где b – любой из параметров газа. , где b – любой из параметров газа.При нестационарном движении газа поверхности разрыва не остаются неподвижными. При этом необходимо подчеркнуть, что скорость движения поверхности разрыва не имеет ничего общего со скоростью движения самого газа. Частицы газа могут при своем движении проходить через эту поверхность, пересекая ее. Скорость движения элемента поверхности в направлении внешней нормаль определяется следующим образом: 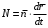 (2), (2), где 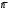 - единичный вектор, направленный из области - единичный вектор, направленный из области 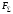 <0 в область <0 в область 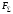 >0. >0.На нашей поверхности, в силу уравнения (1), выполняется соотношение: 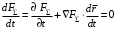 (3). (3).Вектор 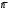 можем выразить в виде: можем выразить в виде: 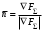 . Тогда из (2), с учетом (3), получим: . Тогда из (2), с учетом (3), получим: 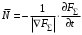 . .Т.е. мы получили скорость поверхности разрыва относительно неподвижной (лабораторной) системы координат. Обозначим через θ скорость распространения поверхности относительно движущихся частиц газа и 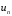 - нормальная к поверхности разрыва составляющая скорости среды. - нормальная к поверхности разрыва составляющая скорости среды.Тогда: 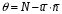 (4) или (4) или 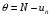 (4). (4).Определим, какие соотношения между газодинамическими величинами должны выполняться на поверхности разрыва для удовлетворения законов сохранения. Рассмотрим физико-математические моменты движения вещества через поверхность разрыва: Во-первых, на поверхности разрыва должен быть непрерывен поток вещества, т.е. количество газа, входящее с одной стороны, должно быть равно количеству газа, выходящего с другой стороны поверхности. Поэтому должно выполняться равенство: 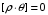 или или 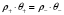 (5). (5).Во-вторых, должен быть непрерывен поток импульса, т.е. должны быть равны силы, с которыми действуют друг на друга газы по обеим сторонам поверхности разрыва: 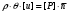 (6), где (6), где 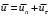 . .В-третьих, должен быть непрерывен поток энергии: 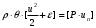 (7). (7).Уравнения (5), (6), (7) называются уравнениями динамической совместимости на поверхности сильного разрыва, т.е., если имеем поверхность разрыва, то газодинамические функции на ней не могут быть произвольными, а должны подчиняться этим уравнениям. Физически это означает выполнение законов сохранения на поверхности сильного разрыва. Поверхности сильного разрыва делятся на два типа: 1. Через поверхность разрыва нет потока вещества, 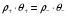 , а т.к. , а т.к. 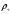 и и 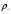 не равны нулю, следовательно, не равны нулю, следовательно, 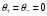 . Тогда из уравнений (5)-(7): . Тогда из уравнений (5)-(7): 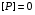 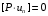 , т.е. , т.е. 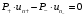 , откуда: , откуда: 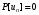 , т.е. , т.е. 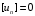 . . Из выражения 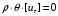 следует, что следует, что 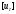 может быть произвольно. Следовательно, могут быть произвольны и другие термодинамические величины, кроме Р. Такие поверхности называются поверхностями контактного или тангенциального или стационарного разрыва. может быть произвольно. Следовательно, могут быть произвольны и другие термодинамические величины, кроме Р. Такие поверхности называются поверхностями контактного или тангенциального или стационарного разрыва.Поток вещества, а, следовательно, и θ – не равен нулю; через поверхность движутся частицы газа. Т.к. 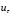 непрерывна на поверхности, то непрерывна на поверхности, то 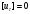 . Поверхность, для которой θ не равен нулю, т.е. для которой Р меняется скачком, называется ударной волной. . Поверхность, для которой θ не равен нулю, т.е. для которой Р меняется скачком, называется ударной волной.Движущаяся ударная волна представляет собой пример нестационарного течения газа; но если неподвижная среда, в которой распространяется ударная волна, сама начала двигаться в направлении, противоположном движению волны с той, же скоростью, то в неподвижной системе координат ударная волна неподвижна, а течение стационарно. Такая ударная волна называется скачком уплотнения. Скачки уплотнения той или иной интенсивности почти всегда присутствуют в движущихся со сверхзвуковой скоростью потоках газа, или при движении в них летящих тел. Рассмотрим цилиндрическую трубу бесконечной длины, вдоль которой перемещается поршень. Газ и поршень вначале неподвижны. 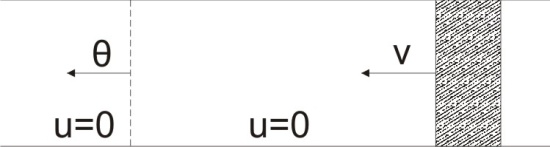 Затем поршень мгновенно приобретает некоторую скорость и начинает перемещаться, сжимая находящийся перед ним газ. Возникающее при этом возмущение в виде сжатия распространяется по трубе. Разобьем область возмущенного газа на большое число объемов с сечениями, перпендикулярными оси трубы. В каждом из объемов имеются свои значения параметров газа и скорости распространения возмущений по отношению к самому газу. Предположим, что распределение возмущений вдоль трубы непрерывно, т.е. параметры газа в рядом находящихся объемах различается незначительно. Применяя теорию малых возмущений, можно утверждать, что скорость распространения возмущений в каждом сечении равна местной скорости звука и всякое повышение давления распространяется в среде в виде волны, движущейся со скоростью звука - акустической волны. Сильные волны распространяются со скоростями, большими скорости звука. Основная особенность сильной ударной волны в том, что фронт в ней очень узок и пропорционален длине свободного пробега молекулы, в связи с чем параметры состояния газа, такие как P, T, ρ меняются скачком. 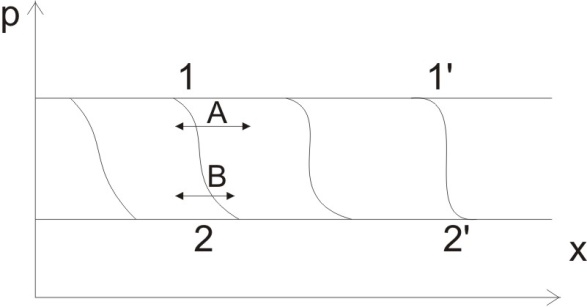 Наклон меняется до тех пор, пока не не образуется вертикальный плоский скачок 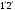 . .Пусть в некоторой области произошло изменение давления и волна имеет плавную форму 1АВ2; на бесконечно узких участках волны давление возрастает незначительно и поэтому распространение такой волны идет со скоростью звука. В области высоких сжатий наблюдаются более высокие температуры, в силу чего “вершина” волны движется быстрее, чем “подножие”. В сторону меньших давлений (вправо) волна распространяется как волна сжатия. В сторону высоких давлений – как волна разряжения. Т.о., даже если вначале волна сжатия была пологой, то со временем она делается все круче. Процесс остановится и волна приобретет устойчивую форму только тогда, когда ее фронт станет плоским 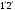 . .Итак, волны сжатия распространяются как скачки давления (разрывы) и их называют ударными. По тем же причинам, вследствие того, что волны разряжения в зоне А движутся быстрее, чем в зоне В, фронт со временем растягивается, т.е. скачки разряжения не образуются.  Имеем цилиндр, в котором находится поршень. В момент страгивания поршня(момент начала движения) в цилиндре по невозмущенному газу побежала волна возмущения, переводя газ из состояния 0 в состояние 1. А поршень движется дальше и в следующий момент времени по газу с параметрами состояния 1 бежит следующая волна, а т.к. 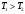 (из уравнения состояния), то волна бежит с большой скоростью, и каждое последующее возмущение догоняет предыдущее, они сходятся в одной точке и в результате образуется разрыв в параметрах состояния. Это есть ударная волна. (из уравнения состояния), то волна бежит с большой скоростью, и каждое последующее возмущение догоняет предыдущее, они сходятся в одной точке и в результате образуется разрыв в параметрах состояния. Это есть ударная волна. |
