Рисола Кенҷаева. Боби i мафуми табдилотои хатт 7 1 Табдилоти хатт ва амало бо оно 7
 Скачать 183.7 Kb. Скачать 183.7 Kb.
|
§2.2 Матритсаҳои Жорданӣ ва муодилаи характеристикии матритсаҳои ЖорданӣДар мавзӯи мазкур матритсаи квадратиро дар майдони ададҳои комплексӣ муоина мекунем. Фарз мекунем, ки матритсаи тартиби 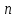 -уми зерин дода шудааст: -уми зерин дода шудааст: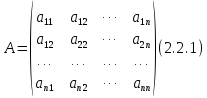 дар ин ҷо 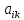 -адади комплексӣ мебошад. -адади комплексӣ мебошад.Матритсаи  -ро матритсаи 𝜆 гуфта қабул мекунем. Дар ҳақиқат адади -ро матритсаи 𝜆 гуфта қабул мекунем. Дар ҳақиқат адади 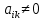 нисбат ба 𝜆 бисёраъзогии дараҷаи нисбат ба 𝜆 бисёраъзогии дараҷаи 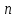 -умро ифода мекунад, дар ҳолати -умро ифода мекунад, дар ҳолати 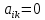 будан, бисёраъзогии дараҷаи нулиро ифода мекунад. Матритсаи будан, бисёраъзогии дараҷаи нулиро ифода мекунад. Матритсаи  , ки аз ададҳо иборат аст, ҳолати хусусии матритсаи 𝜆 мебошад ва онро матритсаи тағйирнаёбанда меноманд. Аз ҳама намуди содаи матритсаи тағйирнаёбанда ин матритсаи диагоналӣ аст: , ки аз ададҳо иборат аст, ҳолати хусусии матритсаи 𝜆 мебошад ва онро матритсаи тағйирнаёбанда меноманд. Аз ҳама намуди содаи матритсаи тағйирнаёбанда ин матритсаи диагоналӣ аст: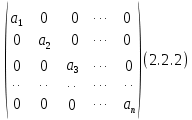 дар ин ҷо 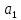 , , 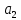 , , 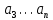 -ҳо ададҳои комплексӣ мебошад. -ҳо ададҳои комплексӣ мебошад.Инчунин матритсаҳои хоначаи Жордантро низ меомӯзем. Таърифи 1. Матритсаи зерин, ки 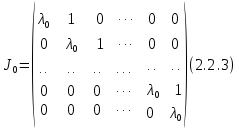 нисбат ба 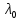 матритсаи тартиби матритсаи тартиби 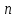 -умро ифода мекунад, хоначаи Жорданӣ номида мешавад. Масалан, матритсаи -умро ифода мекунад, хоначаи Жорданӣ номида мешавад. Масалан, матритсаи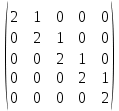 хоначаи Жордании тартиби 5 аз рӯи 2, ёки матритсаи 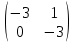 бошад, ба адади -3 тааллуқ дорад ва тартиби матритсаи Жорданӣ ба 2 баробар аст. Дар ҳолати хусусӣ хоначаи Жордании тартибаш як шуданаш ҳам мумкин аст. Масалан, матритсаи ( 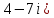 катаки ба матритсаи катаки ба матритсаи 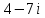 тааллуқ дорад. тааллуқ дорад.Таърифи 2. Диагонали асосии матритсаҳо 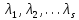 буда ва болояш буда ва болояш 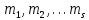 бошад, ба хоначаи бошад, ба хоначаи 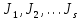 тааллуқ дорад ва боқимонда элементҳояш аз нулҳо иборат бошад, ин гуна матритсаро матритсаи Жорданӣ меноманд. тааллуқ дорад ва боқимонда элементҳояш аз нулҳо иборат бошад, ин гуна матритсаро матритсаи Жорданӣ меноманд.Дар вақти навишти хоначаҳои Жорданӣ элементҳои нулҳоро партофта, боқимонда элементҳоро мегирем ва ба таври зерин менависем: 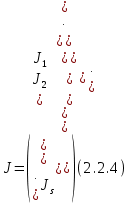 Дар ин ҷо 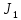 ба матритсаи тартиби ба матритсаи тартиби 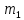 ва ва 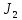 ба матритсаи тартиби ба матритсаи тартиби 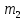 баробар буда, ба баробар буда, ба 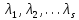 -ҳо тааллуқ дорад. Дар ин ҷо ададҳои -ҳо тааллуқ дорад. Дар ин ҷо ададҳои 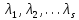 ба ададҳои ба ададҳои 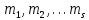 баробар бошад, баробар бошад, 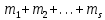 = =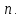 Масалан: 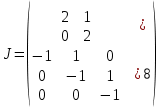 Матритсаи Жордании тартиби 6-и зерин: аз хоначаҳои тартиби 2 оид ба 2, тартиби 3 аз рӯи -1 ва тартиби 1 аз рӯи 8 тартиб дода шудааст. Муодилаи характеристикии матритсаи Жорданӣ. Барои тартиб додани муодилаи характеристикии хоначаи 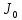 -и Жорданӣ, дар диагонали асосӣ аз -и Жорданӣ, дар диагонали асосӣ аз 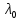 𝜆-ро тарҳ мекунем. Матритсаи характеристикии хоначаи Жорданиро дар намуди зерин ҳосил мекунем: 𝜆-ро тарҳ мекунем. Матритсаи характеристикии хоначаи Жорданиро дар намуди зерин ҳосил мекунем: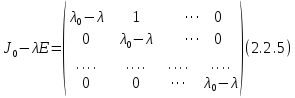 матритсаи ҳосилшуда аз 𝜆 матритса иборат аст. 𝜆-матритсаро ба намуди нормалӣ меорем. Аз шакли 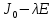 ифодаи зеринро ҳосил мекунем: ифодаи зеринро ҳосил мекунем: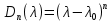 Пас, дар 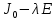 сутуни якум ва сутуни якум ва 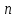 -умро хат зада, минори тартиби -умро хат зада, минори тартиби ( 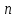 -1)-ро ҳосил мекунем: -1)-ро ҳосил мекунем: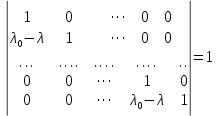 мебошад. Дар ин ҷо калонтарин тақсимкунандаи умумии тартиби 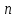 -1 ба як баробар аст, яъне натиҷаи зерин бармеояд: -1 ба як баробар аст, яъне натиҷаи зерин бармеояд: 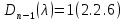 Бисёраъзогии 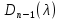 ба бисёраъзогии ба бисёраъзогии 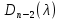 тақсим мешавад, ин алгоритмро давом медиҳем, дар натиҷа тақсим мешавад, ин алгоритмро давом медиҳем, дар натиҷа 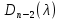 ба ба 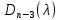 ... ва ғайраҳо ҳосил мешавад. ... ва ғайраҳо ҳосил мешавад.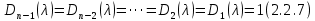 Аз ифодаи ҳосил шуда баробариҳои зеринро тартиб медиҳем: 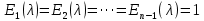 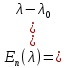 Матритсаи Жорданиро ба намуди нормалии диагоналӣ меорем: 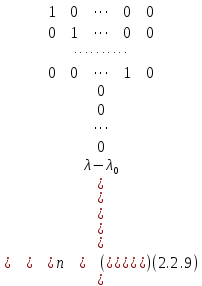 Теоремаи 1. Ҳар як матритсаи ихтиёриро бо ёрии табдилотҳои элементарии матритсаҳо ба намуди диагоналҳо овардан мумкин аст. Дар ин ҷо аз хосиятҳои табдилотҳои элементарии матритсаҳо истифода мебарем. Матритсаҳои характеристикии матритсаҳоиЖорданӣ Фарз мекунем, ки матритсаи Жордании зерин дода шудааст: 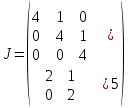 Дар ин ҷо як матритсаи хоначаи Жордании тартиби 3, матритсаи хоначаи Жордании тартиби 2 ва матритсаи хоначаи Жордании тартиби 1-ум мавҷуд аст. Инҳоро алаҳида-алоҳида ҷудо карда, ифодаҳои зеринро ҳосил мекунем: 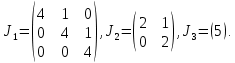 Аз матритсаҳои ҳосилшуда муодилаҳои характеристикӣ тартиб медиҳем: 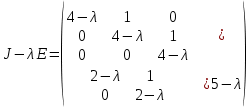 ин хоначаҳои Жорданӣ матритсаҳои зеринро ифода мекунад: 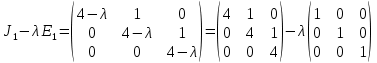 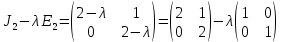 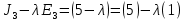 Аз ин матритсаҳо маълум мешавад, ки тартиби матритсаи воҳидии 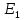 ба тартиби матритсаи ба тартиби матритсаи 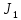 баробар аст.Ин ҷараёнро давом дода, ҳосил мекунем, ки тартиби матритсаи воҳидии баробар аст.Ин ҷараёнро давом дода, ҳосил мекунем, ки тартиби матритсаи воҳидии 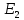 ба тартиби матритсаи Жордании ба тартиби матритсаи Жордании 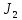 ва тартиби матритсаи воҳидии ва тартиби матритсаи воҳидии 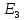 ба тартиби матритсаи ба тартиби матритсаи 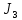 баробар аст. Аз рӯи мисолҳои дар боло қайдшуда, муодилаи характеристикии матритсаи Жорданиро ба таври зерин ифода мекунем: баробар аст. Аз рӯи мисолҳои дар боло қайдшуда, муодилаи характеристикии матритсаи Жорданиро ба таври зерин ифода мекунем: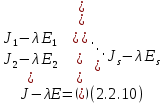 дар ин ҷо тартиби матритсаи воҳидии 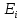 , ба тартиби , ба тартиби 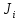 , яъне ба , яъне ба 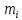 баробар аст. Исботи баробар аст. Исботи 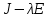 -ро барои ба шакли диагоналии нормалӣ овардан аз леммаи зерин истифода мебарем. -ро барои ба шакли диагоналии нормалӣ овардан аз леммаи зерин истифода мебарем.Лемма. Аз бисёраъзогиҳои зерин 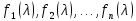 аққалан дутояш байни ҳам сода бошад, матритсаҳои зерин: аққалан дутояш байни ҳам сода бошад, матритсаҳои зерин: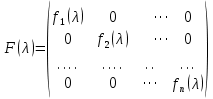 ва ва 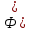 𝜆)= 𝜆)=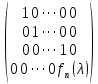 эквивалент мебошад ва 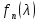 = =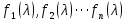 Исбот: Барои бисёраъзогиҳои эквиваленти 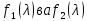 бисёраъзогиҳои бисёраъзогиҳои 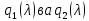 мавҷуд буда, он баробарии мавҷуд буда, он баробарии 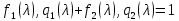 -ро ҳосил мекунад. -ро ҳосил мекунад.Сутуни 1-уми матритсаи 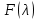 -ро ба -ро ба 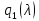 зарб зада, ба сутуни зарб зада, ба сутуни 2-юм ҷамъ мекунем, сутуни 2-и матритсаи 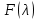 -ро ба -ро ба 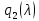 зарб зада, ба сатри якум ҷамъ мекунем ва матритсаи зеринро ҳосил мекунем: зарб зада, ба сатри якум ҷамъ мекунем ва матритсаи зеринро ҳосил мекунем: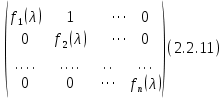 Сутуни якум ва дуюми матритсаи (2.2.11)-ро иваз мекунем ва аз матритсаи ҳосилшуда, ба сутуни якум 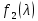 -ро зарб карда, ба сутуни дуюм ҷамъ мекунем, ин ҷараёнро давом дода, матритсаи зеринро ҳосил мекунем: -ро зарб карда, ба сутуни дуюм ҷамъ мекунем, ин ҷараёнро давом дода, матритсаи зеринро ҳосил мекунем: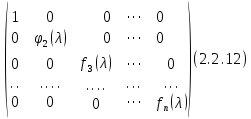 дар ин ҷо 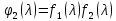 мебошад. мебошад.Азбаски 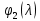 ва ва 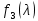 байни ҳам соддаанд, алгоритми дар боло иҷрошударо пай дар пай такрор мекунем ва матритсаи зерин пайдо мегардад: байни ҳам соддаанд, алгоритми дар боло иҷрошударо пай дар пай такрор мекунем ва матритсаи зерин пайдо мегардад: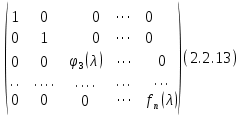 дар ин ҷо 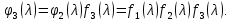 Ин ҷараёнро то матритсаи 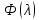 ҳосил шудан такрор мекунем. Азбаски дар ин ҷо матритсаи ҳосил шудан такрор мекунем. Азбаски дар ин ҷо матритсаи 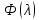 аз матритсаи аз матритсаи 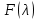 бо ёрии табдилотҳои элементарии матритсаҳо ҳосил шудаанд, пас ин ду матритса эквивалент буда, 𝜆-матритсаро ифода мекунад. бо ёрии табдилотҳои элементарии матритсаҳо ҳосил шудаанд, пас ин ду матритса эквивалент буда, 𝜆-матритсаро ифода мекунад.Мисоли 1. Муодилаи характеристикии матритсаи Жорданиро тартиб диҳед. 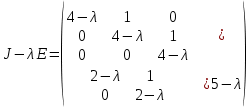 а) 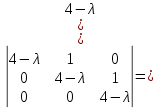 ёки ёки 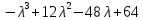 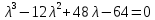 б) 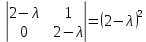 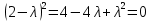 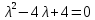 в) 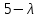 ёки ёки 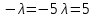 Дар матритсаи (2.2.10) якто 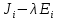 сатр ва сутунҳои сатр ва сутунҳои 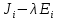 табдилотҳои элементарии матритсаҳоро татбиқ мекунем, дар натиҷа матритса намуди зеринро мегирад: табдилотҳои элементарии матритсаҳоро татбиқ мекунем, дар натиҷа матритса намуди зеринро мегирад: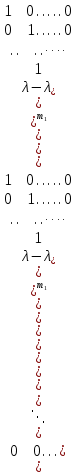 дар ин ҷо нулҳоро наменависем. Аз 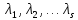 -ҳо байни ҳам баробарҳояш низ мавҷуданд. Агар -ҳо байни ҳам баробарҳояш низ мавҷуданд. Агар 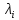 -ҳо баробар бошад, онҳо дар намуди қаторҳои зерин оварда мешавад: -ҳо баробар бошад, онҳо дар намуди қаторҳои зерин оварда мешавад: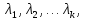 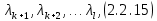 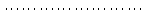 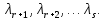 Ҳамин тавр, 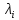 -ҳои дар як сатр ҷойгиршуда байни ҳам баробар буда, элементҳои дар сатрҳои ҳархела бошад, ададҳои ҳархеларо тартиб медиҳад. -ҳои дар як сатр ҷойгиршуда байни ҳам баробар буда, элементҳои дар сатрҳои ҳархела бошад, ададҳои ҳархеларо тартиб медиҳад.Аз тарафи дуюм 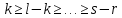 , яъне миқдори , яъне миқдори 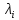 -ҳои дар як сатр хобида, аз адади дар сатри дуюм хобида калон мебошанд ва он нобаробариҳои зеринро қонеъ мегардонад: -ҳои дар як сатр хобида, аз адади дар сатри дуюм хобида калон мебошанд ва он нобаробариҳои зеринро қонеъ мегардонад: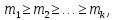 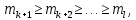  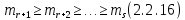 Дар матритсаи (2.2.14) элементҳои дар диагонали асосии аз як фарқкунандароба таври зерин менависем: 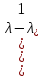 , , 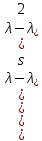 Пас, элементҳои додашударо бо тартиби зерин менависем: 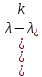 , , 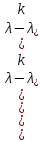 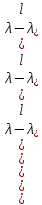  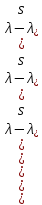 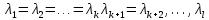 Мисоли 2. Матритсаи характеристикии тартиби 15-ро ба шакли диагоналии нормалӣ оред. 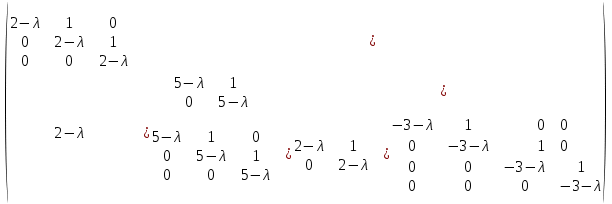 Барои тартиб додани шакли диагоналии матритсаи характеристикӣ аз формулаҳои (2.2.17) истифода мебарем. Дар матритсаи додашуда хоначаҳои Жордании тартиби 3, 2, 1 мавҷуданд ва зиёде аз хоначаҳо оиди 2 мебошанд.Пас, тартиби панҷумро ба тартиби 3 ва 2 меорем. Хоначаи ба -3 тааллуқ доштаро ба 4 меорем. Барои матритсаи додашуда ҷадвали (2.2.17) намуди зеринро мегирад: 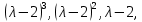 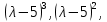 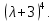 Аз ифодаҳои ҳосилшуда зарбшавандаҳои зеринро ҳосил мекунем: 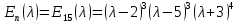 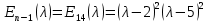 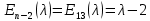 азбаски 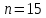 ва ва 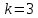 аст, пас: аст, пас: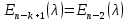 = =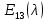 Шакли нормалии ин матритсаро тартиб медиҳем: 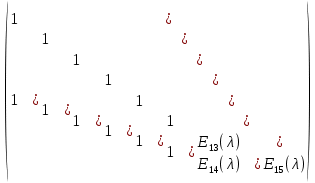 Овардани матритсаи ихтиёрӣбаматритсаиЖорданӣ. Таърифи 3. Агар барои ду матритсаи тартиби 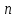 -уми -уми 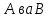 баробарии баробарии 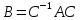 ҷой дошта бошад, он гоҳ матритсаҳои ҷой дошта бошад, он гоҳ матритсаҳои 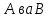 -ро матритсаҳои монанд меноманд. -ро матритсаҳои монанд меноманд.Хосиятҳои асосии матритсаҳои монанд: Хосияти рефлексивӣ. Ҳар як матритсаи  ба худ монанд аст. ба худ монанд аст.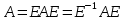 Хосияти симметрикӣ.Агар матритсаи  ба матритсаи ба матритсаи 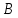 монанд бошад, он гоҳ матритсаи монанд бошад, он гоҳ матритсаи 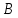 низ ба матритсаи низ ба матритсаи  монанд аст. монанд аст.Хосияти транзитивӣ. Агар матритсаи  ба матритсаи ба матритсаи 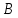 ва матритсаи ва матритсаи 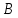 ба матритсаи ба матритсаи 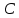 монанд бошад, матритсаи монанд бошад, матритсаи  ба ба 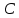 монанд аст. монанд аст.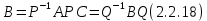 Дар ҳақиқат аз баробарии 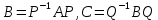 ифодаҳои зеринро ҳосил мекунем: ифодаҳои зеринро ҳосил мекунем: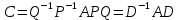 дар ин ҷо 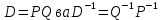 аст. аст.Лемма. Барои бисёраъзогии дараҷаи -уми матритсаи 𝜆 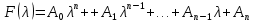 ва ва 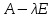 баробарии зерин ҷой дорад: баробарии зерин ҷой дорад: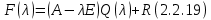 Исбот. Фарз мекунем, ки матритсаи дараҷааш 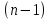 калон набошад. калон набошад.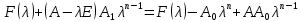 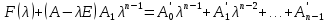 меҳисобем. 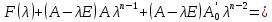 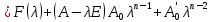 дараҷаи ин матритса аз ( 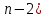 калон намебошад. калон намебошад.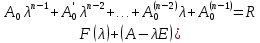 дар ин ҷо матритсаи 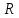 матритсаи доимӣ аст. Дохили қавсҳоро бо матритсаи доимӣ аст. Дохили қавсҳоро бо 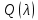 ишорат карда, баробарии зеринро ҳосил мекунем: ишорат карда, баробарии зеринро ҳосил мекунем: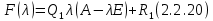 Мисоли 3. Аз рӯи ифодаҳои зерин: 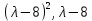 ( 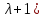 ( 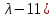 матритсаи Жорданиро тартиб диҳед. Ҳал: Аввал аз рӯи ифодаҳои додашуда матритсаи зеринро тартиб медиҳем: 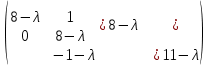 пас, матритсаи Жорданиро тартиб медиҳем: 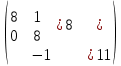 Мисоли 4. Матритсаи ихтиёриро ба матритсаи Жорданӣ оред. 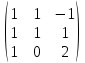 Ҳал: Бисёраъзогии характеристикиро тартиб медиҳем: 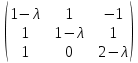 Муайянкунандаи онро ҳал карда, онро ба зарбкунандаҳои дараҷаи якум ҷудо мекунем: 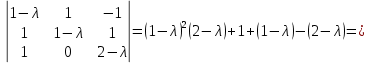 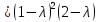 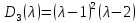 Минори тартиби дуюмро ҳисоб мекунем: 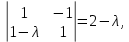 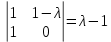 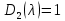 , , 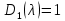 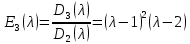 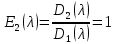 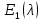 = =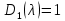 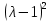 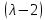 пас, матритсаи зеринро тартиб медиҳем:  Хулоса Дар вақти навиштани рисолаи хатм адабиётҳои асосӣ ва адабиётҳои иловагии аз тарафи омӯзгор тавсияшударо омӯхтам. Мақсади асосии рисолаи хатм ба омӯзиши “Намуди каноникии табдилоти хаттии ихтиёрӣ” буд, ки он масъалаҳои асосии алгебраи хаттиро дар бар мегирад. Рисолаи хатми мазкури навишташуда аз муқаддима, ду боб, чор зербоб, хулоса ва аз адабиётҳои истифодашуда иборат аст. Дар боби якум мафҳуми табдилотҳои хаттӣ, амалҳо бо табдилотҳои хаттӣ, хосиятҳои табдилотҳои хаттӣ муоина карда шудааст. Инчунин дар зербоби 2 мафҳуми векторҳои хос ва қиматҳои хоси зерифазои инвариантӣ, матритсаҳои диагоналӣ ва тартиб додани муодилаи характеристикии вектори хос ва ҳисоб намудани қимати хоси муодилаи характеристикӣ ва намудҳои табдилотҳои хаттӣ омӯхта шудааст. Боби дуюм ба омӯзиши намуди каноникии табдилоти хаттии ихтиёрӣ бахшида шудааст. Дар ин боб шакли нормалии табдилоти хаттӣ, 𝜆 - матритсаҳо, табдилотҳои элементарии намуди каноникии 𝜆-матритсаҳо муоина карда шудааст.Инчунин маълумотҳо доир ба матритсаҳои Жорданӣ, таърифи матритсаи Жорданӣ, муодилаи характеристикии хоначаи Жорданӣ ва тартиб додани он омӯхта шудааст. Ба ҳамаи бобҳо мисолҳо оварда шудааст. Дар вақти навиштани рисола аз бисёр адабиёт истифода бурдам. Масалан: И. М. Гелфанд. ”Лексияҳо аз алгебраи хаттӣ” аз 92-105, 108-120, 199-215. Р. Искандаров. “Олий алгебра” қисми II 125-143. АдабиётГантмахер Ф. Р. Теория матриц. – Москва: Наука, 1966. – 256с Гелфанд И. М. Лексияҳо аз алгебраи хаттӣ. – Душанбе: Маориф, 1991. – 279с Гельфанд И. М. Лекции по линейной алгебре. – Москва: Наука, 1971. – 280с Искандаров Р. И. Олий алгебра. – Тошкент: Ӯрта ва олий таълим, 1961. – 168с Ким, Г. Д. Линейная алгебра и аналитическая геометрия - Москва, 2005. – 450с Курош А. Г. Олий алгебра курси. – Тошкент: Ӯқитувчи, 1976. – 463с Фаддеев Д. К. Лекции по алгебре. – Москва: Наука, 1984. – 241с Халмош П. Конесномерные векторные пространства. – Москва: Физматгиз, 1963. – 302с Хорн Р., Джонсон Ч. Матричный анализ. – Москва: Мир, 1989. – 288с Шафаревич И. Р., Ремизов А. О. Линейная алгебра и геометрия, – Москва: Физматлит, 2009. – 441с |
