Рисола Кенҷаева. Боби i мафуми табдилотои хатт 7 1 Табдилоти хатт ва амало бо оно 7
 Скачать 183.7 Kb. Скачать 183.7 Kb.
|
Боби II. Намуди каноникии табдилоти хаттии ихтиёрӣ§2.1 Табдилоти нормалӣ ва шакли нормалии табдилоти хаттӣДар ин боб масъалаи табдилоти нормалӣ ва шакли нормалии табдилоти хаттии ихтиёрӣ муоина карда шудааст.Дар он 𝜆- матритсаҳо, матритсаҳои монанд, хосиятҳои асосии матритсаҳои монанд ва ба шакли нормалӣ овардани матритсаи ихтиёрӣ, овардани матритсаи ихтиёрӣ ба матритсаи Жорданӣ мушаххас омӯхта шудааст. Таърифи 1. Агар табдилоти  -и фазои унитарӣ шарти -и фазои унитарӣ шарти 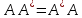 -ро қаноат кунонад, он гоҳ ин табдилотро табдилоти нормалӣ меноманд. -ро қаноат кунонад, он гоҳ ин табдилотро табдилоти нормалӣ меноманд.Масалан, табдилоти ба худ ҳамроҳшуда ва табдилоти унитарӣ ҳолатҳои хусусии табдилоти нормалӣ мебошанд. Теоремаи 1. Барои он ки базиси ортогоналие мавҷуд бошад, ки дар он табдилоти хаттии  ба шакли диагоналӣ оварда мешавад, зарур ва кифоя аст, ки ба шакли диагоналӣ оварда мешавад, зарур ва кифоя аст, ки 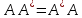 бошад. Исбот. Шарти зарурӣ.Фарз мекунем, ки дар ягон базиси ортонормиронидашуда матритсаи табдилоти  диагоналӣ аст, яъне дар намуди зерин оварда мешавад: диагоналӣ аст, яъне дар намуди зерин оварда мешавад: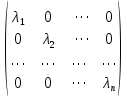 Аз сабабе ки базиси додашуда ортонормиронидашуда мебошад, бинобар ин матритсаи табдилоти 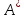 намуди зеринро дорад: намуди зеринро дорад: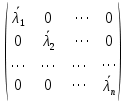 Матритсаҳои табдилоти  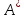 диагоналианд, бинобар ҳамин онҳо байни худ ҷойивазкунанда мебошанд. Пас, худи табдилоти диагоналианд, бинобар ҳамин онҳо байни худ ҷойивазкунанда мебошанд. Пас, худи табдилоти 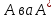 низ ҷойивазкунанда аст. низ ҷойивазкунанда аст.Шарти кифоягӣ. Фарз мекунем, ки: 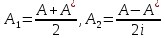 мебошад. Табдилоти 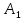 ва ва 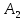 ба худ ҳамроҳшудаанд. Агар ба худ ҳамроҳшудаанд. Агар  ва ва 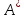 ҷойивазкунанда бошанд, он гоҳ ҷойивазкунанда бошанд, он гоҳ 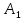 ва ва 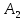 низ ҷойивазкунанда мебошанд. Табдилоти низ ҷойивазкунанда мебошанд. Табдилоти 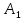 ва ва 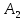 -ро дар як вақт ба шакли диагоналӣ овардан мумкин аст. Он гоҳ -ро дар як вақт ба шакли диагоналӣ овардан мумкин аст. Он гоҳ 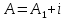 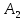 ҳам дар шакли диагоналӣ навишта мешавад. Агар ҳам дар шакли диагоналӣ навишта мешавад. Агар  табдилоти бахуд ҳамроҳшуда бошад, он гоҳ табдилоти бахуд ҳамроҳшуда бошад, он гоҳ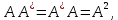 яъне  нормалӣ мебошад. нормалӣ мебошад.Базиси табдилоти ихтиёриро дида мебароем, ки дар он матритсаи ин табдилот намуди нисбатан сода дорад ва шакли нормалии жорданӣ номида мешавад. Вақте ки миқдори векторҳои хаттӣ новобастаи табдилот ба ченаки фазо баробар мешавад, ин шакли нормалӣ ба шакли диагоналӣ оварда мувофиқ меояд. Фарз мекунем, ки табдилоти хаттии ихтиёрии  дар фазои комплексии дар фазои комплексии 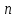 -ченака дода шудааст. Бигузор -ченака дода шудааст. Бигузор 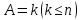 вектори хоси хаттӣ новобастаи вектори хоси хаттӣ новобастаи 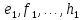 дошта бошад, ки онҳо ба қимати дошта бошад, ки онҳо ба қимати 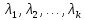 мувофиқанд. Он гоҳ базисе мавҷуд аст, ки аз мувофиқанд. Он гоҳ базисе мавҷуд аст, ки аз 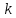 гурӯҳи векторҳои гурӯҳи векторҳои 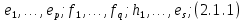 иборат буда, дар он табдилоти  намуди зеринро дорад: намуди зеринро дорад: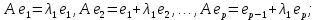 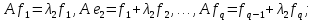 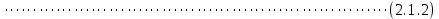 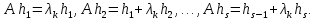 Чӣ тавре ки маълум аст, векторҳои базисии ҳар як гурӯҳ дар вақти табдилот ба комбинатсияи хаттии векторҳои ҳамин гурӯҳ мегузаранд.Аз ин ҷо чунин хулоса баровардан мумкин аст, ки ҳар як гурӯҳи векторҳои базисӣ зерфазоеро ба вуҷуд меоварад, ки он нисбат ба табдилоти  инвариантӣ мебошад. инвариантӣ мебошад.Матритсаи табдилоти (2.1.2)-ро тартиб медиҳем.Азбаски векторҳои ҳар як гурӯҳ бо комбинатсияҳои хаттии векторҳои ҳамин гурӯҳ табдил мешаванд, бинобар ҳамин дар 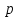 сутуни якуми матритсаи табдилот фақат элементҳои сутуни якуми матритсаи табдилот фақат элементҳои 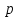 сатри якум аз нул фарқ карда мешаванд. Дар сатри якум аз нул фарқ карда мешаванд. Дар 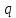 сутуни боқимонда фақат элементҳои сатрҳои рақамашон бо рақами ин сутунҳо якхела аз нул фарқ мекунанд. Ҳамин тариқ дар ин базис матритсаи табдилот аз сутуни боқимонда фақат элементҳои сатрҳои рақамашон бо рақами ин сутунҳо якхела аз нул фарқ мекунанд. Ҳамин тариқ дар ин базис матритсаи табдилот аз 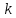 хонача иборат мешавад, ки онҳо дар диагонали асосӣ ҷоқгир шудаанд. Ҳамаи элементҳои ба ин хоначаҳо дохилнашуда ба нул баробаранд. хонача иборат мешавад, ки онҳо дар диагонали асосӣ ҷоқгир шудаанд. Ҳамаи элементҳои ба ин хоначаҳо дохилнашуда ба нул баробаранд.Барои фаҳмидани он ки дар ҳар як хоначаи матритсаи табдилоти  чӣ ҷой гирифтааст, чӣ гуна табдил ёфтани векторҳои як гурӯҳро бори дигар навиштан кифоягӣ мекунад: чӣ ҷой гирифтааст, чӣ гуна табдил ёфтани векторҳои як гурӯҳро бори дигар навиштан кифоягӣ мекунад: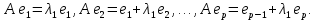 Матритсаи ба табдилоти базис мувофиқро Матритсаи ба табдилоти базис мувофиқро  сохта, хоначаи матритсаи ба гурӯҳи додашудаи векторҳо мувофиқро дар намуди зерин ҳосил мекунем: сохта, хоначаи матритсаи ба гурӯҳи додашудаи векторҳо мувофиқро дар намуди зерин ҳосил мекунем: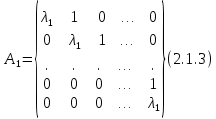 Тамоми матритса низ аз чунин хоначаҳои тартибашон мувофиқан 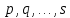 ташкил ёфтааст, яъне намуди зеринро дорад: ташкил ёфтааст, яъне намуди зеринро дорад: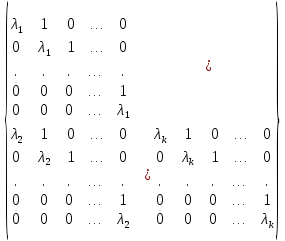 Дар ин ҷо элементҳои берун аз хоначаҳо аз нул иборат аст. Ба шакли нормалӣоварданитабдилотиихтиёрӣ.Акнун мо усули сохтани базисеро меомӯзем, ки дар он матритсаи табдилоти  шакли нормалии жорданӣ дорад.Ин базисро мо бевосита аз векторҳои хос ва пайвастшуда интихоб мекунем. шакли нормалии жорданӣ дорад.Ин базисро мо бевосита аз векторҳои хос ва пайвастшуда интихоб мекунем.Векторҳоихосвавекторҳоипайвастшудаитабдилотихаттӣ.Фарз мекунем, ки 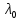 ягон қимати хоси табдилоти ягон қимати хоси табдилоти  мебошад. мебошад.Таърифи 2. Агар 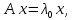 яъне ( яъне (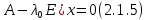 бошад, вектори 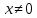 вектори хоси табдилоти вектори хоси табдилоти  -и ба қимати хоси -и ба қимати хоси 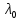 мувофиқ номида мешавад. мувофиқ номида мешавад.Ҳамаи векторҳоро, ки шарти (2.1.5)-ро қаноат мекунонад, барои 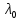 -и қайдшуда дида мебароем. Чӣ тавре ки ба мо маълум аст, ҷамъбасти ин векторҳо зерифазои фазои -и қайдшуда дида мебароем. Чӣ тавре ки ба мо маълум аст, ҷамъбасти ин векторҳо зерифазои фазои 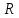 мебошад. Ин зерифазоро бо мебошад. Ин зерифазоро бо 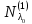 ишора мекунем. ишора мекунем.Қайд мекунем, ки зерифазои 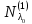 аз ҳамаи векторҳои хоси табдилоти аз ҳамаи векторҳои хоси табдилоти  -и ба қимати хоси -и ба қимати хоси 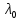 мувофиқ иборат буда, ба онҳо вектори нулӣ ҳамроҳ карда шудааст. мувофиқ иборат буда, ба онҳо вектори нулӣ ҳамроҳ карда шудааст.Таърифи 3. Агар вектори 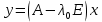 вектори хоси табдилоти вектори хоси табдилоти  бошад, вектори бошад, вектори 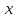 вектори пайвастшудаи тартиби якуми табдилоти вектори пайвастшудаи тартиби якуми табдилоти  -и ба қимати хоси -и ба қимати хоси 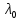 мувофиқ номида мешавад. мувофиқ номида мешавад.Агар ба зерифазои 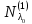 векторҳои пайвастшудаи тартиби якумро илова кунем, зерифазои векторҳои пайвастшудаи тартиби якумро илова кунем, зерифазои 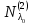 ҳосил мешавад. ҳосил мешавад.Ба мисли ҳамин зерифазои 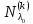 -ро ворид мекунем, ки он аз ҳамаи векторҳои -ро ворид мекунем, ки он аз ҳамаи векторҳои 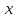 , ки барои онҳо шарти , ки барои онҳо шарти 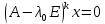 иҷрошаванда аст. Таърифи 4. Агар вектори 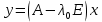 вектори пайвастшудаи тартиби вектори пайвастшудаи тартиби 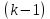 -ум бошад, вектори -ум бошад, вектори 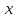 вектори пайвастшудаи тартиби вектори пайвастшудаи тартиби 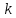 -ум номида мешавад. -ум номида мешавад.Ба ибораи дигар, векторе ки ба 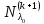 тааллуқ дошта, ба тааллуқ дошта, ба 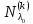 тааллуқ надорад, вектори пайвастшудаи тартиби тааллуқ надорад, вектори пайвастшудаи тартиби 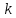 -ум номида мешавад. -ум номида мешавад.Ба шакли нормалӣ овардани матритсаи дорои як қимати хос. Агар табдилоти хаттӣ танҳо аз векторҳои хос иборат бошад, дар ин фазо базисро ихтиёрӣ қабул кардан мумкин аст ва матритсаи табдилот дар ин базис намуди диагоналӣ дорад. Барои интихоб кардани базис, ки дар он матритсаи табдилоти хаттӣ намуди нисбатан соддатар дорад, мо занҷирчаи векторҳои хос ва пайвастшударо кашола мекунем. Барои ин дар зерифазои 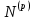 ягон базисро интихоб намуда, ба векторҳои ин базис табдилоти ягон базисро интихоб намуда, ба векторҳои ин базис табдилоти  -ро пай дар пай татбиқ татбиқ менамоем. -ро пай дар пай татбиқ татбиқ менамоем.Таърифи 5. Системаи 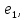 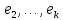 -и векторҳои хаттӣ новобастаи -и векторҳои хаттӣ новобастаи 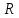 , ки баъди бо ягон базиси , ки баъди бо ягон базиси 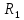 пурра шудан, базиси тамоми фазоро ташкил медиҳад, базиси фазои пурра шудан, базиси тамоми фазоро ташкил медиҳад, базиси фазои 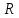 нисбат ба зерифазои нисбат ба зерифазои 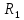 номида мешавад. номида мешавад.Тасаввур мекунем, ки табдилоти  дар фазои дар фазои 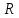 танҳо як қимати хос дорад. Умумияти онро маҳдуд накарда, фарз кардан мумкин аст, ки вай ба нол баробар мебошад. Занҷирчаи зерифазои зеринро дида мебароем: танҳо як қимати хос дорад. Умумияти онро маҳдуд накарда, фарз кардан мумкин аст, ки вай ба нол баробар мебошад. Занҷирчаи зерифазои зеринро дида мебароем: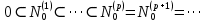 Дар зерифазои максималии зерифазоҳои 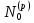 нисбат ба зерифазои онро дарбаргиранди нисбат ба зерифазои онро дарбаргиранди 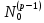 базисеро интихоб мекунем. Бигузор базисеро интихоб мекунем. Бигузор 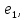 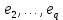 векторҳои ин базис бошанд. Ба мо маълум аст, ки онҳо векторҳои пайвастшудаи тартиби ( 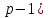 -ум мебошанд.Векторҳои -ум мебошанд.Векторҳои 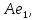 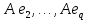 дар вектори дар вектори 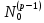 мехобанд. Нишон медиҳем, ки ин векторҳо нисбат ба зерифазои мехобанд. Нишон медиҳем, ки ин векторҳо нисбат ба зерифазои 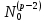 -и дар вектори -и дар вектори 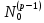 ҷойгиршуда хаттӣ новобаста мебошанд. Дар ҳақиқат, бигузор на ҳамаи ҷойгиршуда хаттӣ новобаста мебошанд. Дар ҳақиқат, бигузор на ҳамаи 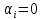 мебошанд ва мебошанд ва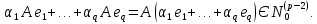 Он гоҳ вектори 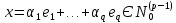 аст. Вале ин ба фарзияти мо, ки векторҳои аст. Вале ин ба фарзияти мо, ки векторҳои 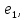 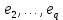 нисбат ба нисбат ба 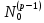 хаттӣ новобаста мебошанд, мухолиф аст. хаттӣ новобаста мебошанд, мухолиф аст. Векторҳои 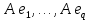 -ро дар -ро дар 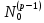 нисбат ба нисбат ба 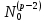 та базис пурра мекунем ва та базис пурра мекунем ва 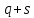 вектори вектори 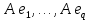 , , 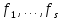 -ро ҳосил менамоем, ки онҳо миқдори максималии векторҳои хаттӣ новобастаи пайвастшудаи тартиби -ро ҳосил менамоем, ки онҳо миқдори максималии векторҳои хаттӣ новобастаи пайвастшудаи тартиби 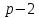 мебошад. мебошад.Векторҳои ҳосилшударо дар ҷадвали зерин ҷойгир менамоем: 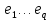 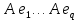 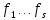 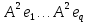 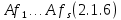   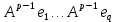 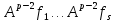 Ҳамаи векторҳои дар ҷадвал овадашуда базиси 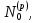 яъне тамоми фазои яъне тамоми фазои 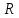 -ро ташкил медиҳанд. -ро ташкил медиҳанд.Нишон медиҳем, ки дар ин базис матритсаи табдилоти  шакли нормалии жорданӣ дорад. Сутуни ихтиёрии ҷадвали (2.1.6), масалан сутуни якумро таҳлил мекунем. шакли нормалии жорданӣ дорад. Сутуни ихтиёрии ҷадвали (2.1.6), масалан сутуни якумро таҳлил мекунем. 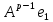 -ро бо -ро бо 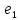 , , 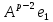 -ро бо -ро бо 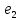 ва ғайра ишора мекунем ва таъсири табдилоти ва ғайра ишора мекунем ва таъсири табдилоти  -ро ба ҳар яки ин векторҳо дида мебароем. Аз сабабе ки -ро ба ҳар яки ин векторҳо дида мебароем. Аз сабабе ки 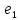 вектори хоси ба қимати хоси нулӣ мувофиқ аст, бинобар ҳамин: вектори хоси ба қимати хоси нулӣ мувофиқ аст, бинобар ҳамин: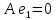 мешавад. Сипас, мувофиқи таъриф 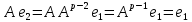 ва мисли ҳамин 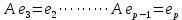 мешавад. мешавад.Ҳамин тавр, табдилоти  векторҳои сутуни якумро боз ба худаш табдил медиҳад, яъне зерифазои векторҳои сутуни якумро боз ба худаш табдил медиҳад, яъне зерифазои 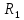 -и бо ин векторҳо ҳосилшуда нисбат ба табдилоти -и бо ин векторҳо ҳосилшуда нисбат ба табдилоти  инвариантӣ мебошад. Намуди матритсаи табдилоти инвариантӣ мебошад. Намуди матритсаи табдилоти  дар зерифазои дар зерифазои 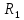 дар базиси дар базиси 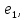 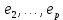 чунин мебошад: чунин мебошад: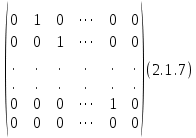 яъне ин хоначаи жорданӣ мебошад, ки ба қимати хоси 𝜆 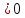 мувофиқ меояд. Зерифазои инвариантии ба ин монанд ба ҳар яке аз сутунҳои ҷадвали (2.1.6) мувофиқ меояд ва ченаки ҳар яке аз ин зерифазоҳо ба адади векторҳои сутуни мувофиқ баробар аст. Азбаски матритсаи табдилоти мувофиқ меояд. Зерифазои инвариантии ба ин монанд ба ҳар яке аз сутунҳои ҷадвали (2.1.6) мувофиқ меояд ва ченаки ҳар яке аз ин зерифазоҳо ба адади векторҳои сутуни мувофиқ баробар аст. Азбаски матритсаи табдилоти  дар базисе, ки аз векторҳои ягон сутуни ҷадвали (2.1.6) иборат аст, намуди (2.1.7)-ро дорад, бинобар ҳамин матритсаи табдилот дар тамоми фазои дар базисе, ки аз векторҳои ягон сутуни ҷадвали (2.1.6) иборат аст, намуди (2.1.7)-ро дорад, бинобар ҳамин матритсаи табдилот дар тамоми фазои 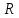 дар базисе, ки аз ҳамаи векторҳои ҷадвали (2.1.6) иборат аст, аз хоначаҳои жорданӣ иборат аст. Миқдори ин хоначаҳо ба миқдори сутунҳои ин ҷадвал баробар буда, ченаки ҳар як хонача ба миқдори векторҳои сутуни мувофиқ баробар мебошад. дар базисе, ки аз ҳамаи векторҳои ҷадвали (2.1.6) иборат аст, аз хоначаҳои жорданӣ иборат аст. Миқдори ин хоначаҳо ба миқдори сутунҳои ин ҷадвал баробар буда, ченаки ҳар як хонача ба миқдори векторҳои сутуни мувофиқ баробар мебошад.Агар ба ҷои табдилоти  табдилоти табдилоти 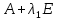 -ро гузорем, он гоҳ хоначаҳои жордании матритсаи табдилоти -ро гузорем, он гоҳ хоначаҳои жордании матритсаи табдилоти 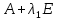 дар намуди зерин навишта мешавад: дар намуди зерин навишта мешавад: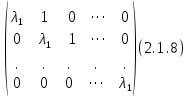 |
