Рисола Кенҷаева. Боби i мафуми табдилотои хатт 7 1 Табдилоти хатт ва амало бо оно 7
 Скачать 183.7 Kb. Скачать 183.7 Kb.
|
Боби I Мафҳуми табдилотҳои хаттӣ1.1 Табдилоти хаттӣ ва амалҳо бо онҳоАзбаски мавзӯи рисолаи хатм ба мафҳуми табдилотҳои хаттӣ вобаста аст, пас аввал маълумотҳо оиди табдилотҳои хаттӣ омӯхта шудааст. Боби якум ба қисми назарияи мафҳуми табдилотҳои хаттӣ бахшида шудааст. Дар ин боб ду зербоб мавҷуд буда, дар он таъриф ва теоремаҳо доир ба табдилотҳои хаттӣ, амалҳо бо табдилотҳои хаттӣ, маълумотҳо гирд оварда шудааст. Инчунин 𝜆-матритсаҳо ва матритсаҳои Жорданӣ ба вектори хос ва қимати хоси табдилотӣ хаттӣ алоқаманд аст, пас тартиб додани бисёраъзогиҳои характеристикии зерфазоҳои инвариантӣ низ омӯхта шудааст. Мо функсияҳоро дар фазои хаттии n-ченака омӯхта будем, ки онҳо қиматҳои ададӣ қабул мекарданд ба онҳо функсияҳои хаттӣ, шаклҳои квадратӣ ва ҳоказо дохил мешаванд.Аммо баъзан ба мо лозим мешавад, ки функсияҳои намуди дигарро омӯзем.Масалан, функсияҳое, ки ба ҳар як нуқтаи фазо боз ягон нуқтаи ин фазоро мувофиқгузорӣ кунем.Яке аз содатарини ин функсияҳо табдилоти хаттӣ мебошанд. Таърифи 1. Фарз мекунем, ки ба ҳар як вектори x-и фазои n-ченака вектори y-и ин фазо мувофиқ гузошта шудааст. Функсияи y 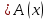 -ро табдилоти фазои R меномем. -ро табдилоти фазои R меномем.Танҳо дар ҳолате, ки шартҳои зерин иҷро шаванд: 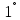 A( A(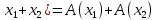 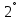 A(λx) A(λx)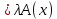 , ,он гоҳ табдилоти A-ро хаттӣ меноманд. Алоқаибайниматрисаҳоватабдилотихаттӣ. Тасаввур мекунем, ки 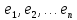 ягон базиси фазои n-ченакаи R ва A табдилоти хаттии R бошад. Барои ҳар гуна n вектори ягон базиси фазои n-ченакаи R ва A табдилоти хаттии R бошад. Барои ҳар гуна n вектори 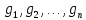 танҳо чунин табдилоти хаттии A мавҷуд аст, ки барои он танҳо чунин табдилоти хаттии A мавҷуд аст, ки барои он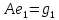 , , 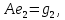 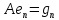 мебошад. Инро исбот мекунем.Нишон медиҳем, ки табдилоти A бо векторҳои 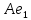 , , 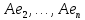 якқимата муайян карда мешавад. Дар ҳақиқат, фарз мекунем, ки якқимата муайян карда мешавад. Дар ҳақиқат, фарз мекунем, ки x 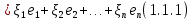 вектори ихтиёрии R мебошад.Аз ин ҷо ҳосил мекунем Ax 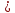 A( A(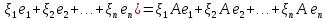 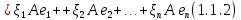 ва бинобар ин Ax бо 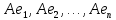 якқимата муайян карда мешавад. якқимата муайян карда мешавад.Месанҷем, ки барои ҳар гуна векторҳои 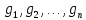 чунин табдилоти хаттии A мавҷуд аст, ки барои он чунин табдилоти хаттии A мавҷуд аст, ки барои он 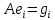 аст. Ба векторҳои аст. Ба векторҳои 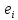 векторҳои векторҳои 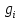 -ро мувофиқ мегузорем; ба вектори ихтиёрии -ро мувофиқ мегузорем; ба вектори ихтиёрии 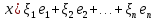 вектори вектори  -ро мувофиқ мегузорем. Азбаски вектори x ба воситаи -ро мувофиқ мегузорем. Азбаски вектори x ба воситаи 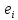 якқимата ифода меёбад, бинобар ҳамин ба он вектори муайяни якқимата ифода меёбад, бинобар ҳамин ба он вектори муайяни 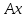 мувофиқ гузошта мешавад. мувофиқ гузошта мешавад.Координатаҳои вектори 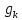 -ро дар базиси -ро дар базиси 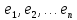 бо бо 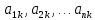 ишора мекунем, яъне фарз мекунем, ки ишора мекунем, яъне фарз мекунем, ки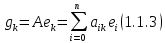 аст. Ҷамъбасти ададҳои 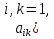 2,…..,n) матритсаи A= 2,…..,n) матритсаи A=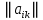 -ро ташкил медиҳад, ки онро мо матритсаи табдилоти хаттии A-и базиси -ро ташкил медиҳад, ки онро мо матритсаи табдилоти хаттии A-и базиси 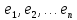 меномем. меномем.Ҳамин тавр мо исбот кардем, ки дар базиси додашудаи 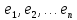 ба ҳар як табдилоти хаттии A матритсаи ба ҳар як табдилоти хаттии A матритсаи 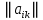 якқимата мувофиқ меояд ва баръакс ба ҳар як матритсаи табдилоти хаттии бо формулаҳои (1.1.1) , (1.1.2) , (1.1.3) ёфташаванда якқимата мувофиқ меояд.Аз ин ҷо хулоса мебарояд, ки табдилоти хаттиро бо ёрии матритсаҳо тасвир кардан мумкин аст, ки бо ёрии онҳо табдилоти хаттӣ дар фазои ченакаш охирнок омӯхта мешаванд. якқимата мувофиқ меояд ва баръакс ба ҳар як матритсаи табдилоти хаттии бо формулаҳои (1.1.1) , (1.1.2) , (1.1.3) ёфташаванда якқимата мувофиқ меояд.Аз ин ҷо хулоса мебарояд, ки табдилоти хаттиро бо ёрии матритсаҳо тасвир кардан мумкин аст, ки бо ёрии онҳо табдилоти хаттӣ дар фазои ченакаш охирнок омӯхта мешаванд.Ҷамъ ва зарби табдилоти хаттӣ.Бо ёрии табдилоти хаттӣ амалҳои ҷамъ ва зарбро иҷро кардан мумкин аст. Таърифи 2.Ҳосили зарби табдилоти хаттии A ва B гуфта табдилоти C-ро меноманд, ки он аз пай дар пай иҷро намудани аввал табдилоти B ва баъд табдилоти A иборат аст, яъне: C=AB чунин маъно дорад, ки барои ҳар гуна x Cx=A(Bx) мебошад. Ҳосили зарби табдилоти хаттӣ табдилоти хаттӣ аст, яъне шартҳои 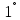 ва ва 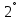 -и таърифи 1-ро қаноат мекунонад.Инро месанҷем: -и таърифи 1-ро қаноат мекунонад.Инро месанҷем: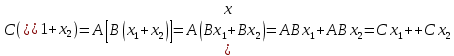 Баробарии якум дар асоси таърифи ҳосили зарб, баробарии дуюм дар асоси хосияти 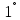 барои барои 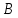 ва баробарии сеюм бошад, дар асоси худи ин хосият барои ва баробарии сеюм бошад, дар асоси худи ин хосият барои  ва дар охир баробарии чорум боз ҳам мувофиқи таърифи ҳосили зарб навишта шудааст.Монанди ҳамин нишон дода шудааст, ки ва дар охир баробарии чорум боз ҳам мувофиқи таърифи ҳосили зарб навишта шудааст.Монанди ҳамин нишон дода шудааст, ки 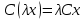 аст. аст.Агар E табдилоти воҳидӣ ва  табдилоти ихтиёрӣ бошад, он гоҳ исбот кардан осон аст, ки табдилоти ихтиёрӣ бошад, он гоҳ исбот кардан осон аст, ки AE=EA=A мебошад. Одатан дараҷаҳои табдилоти A-ро муайян мекунем: 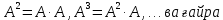 Чун барои ададҳо мувофиқи таъриф 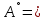 E ҳисоб мекунем. Маълум аст, ки E ҳисоб мекунем. Маълум аст, ки 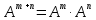 мебошад. мебошад.Таърифи 3.Суммаи табдилоти хаттии A ва B гуфта табдилоти C-ро меноманд, ки он ба ҳар як вектори x вектори Ax+Bx-ро мувофиқ мегузорад; ба ибораи дигар, C=A+B чунин маъно дорад, ки барои ҳар гуна x Сx 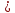 Ax+Bx мебошад. Ax+Bx мебошад.Ҷамъ ва зарби табдилоти хаттӣ хосиятҳои ҷамъ ва зарбро қаноат мекунонад, чунончи: 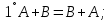 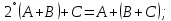 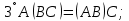 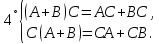 Байни табдилоти хаттӣ ва матритсаҳо мувофиқати якқимата муқаррар карда шудааст, илова бар ин ба сумма сумма ва ба ҳосили зарб ҳосили зарб мувофиқат мекунад. Инро исбот мекунем: Бигзор матритсаи A= 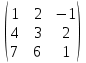 ва B ва B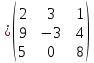 бошад, бошад, A+B A+B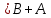 буданашро месанҷем: буданашро месанҷем:A+B 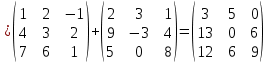 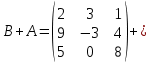 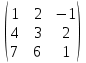 = =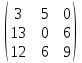 Аз ин ҷо дидан мумкин аст, ки A+B 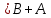 . .Зарби табдилоти хаттӣ, умуман, ғайрикоммутативӣ аст. Инро дар мисоли матритсаҳо санҷидан мумкин аст: Барои зарби матритсаҳо аз қоидаи зарби матритсаҳо истифода мебарем: 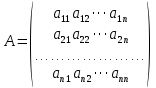 ; ; 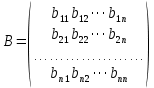 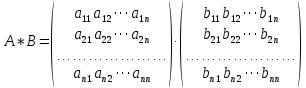 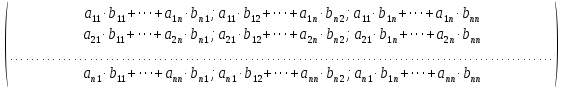 Як мисол пешкаш менамоем: A= 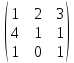 ва B ва B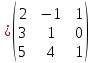 A 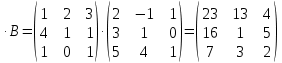 ва ва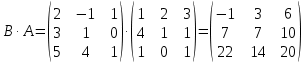 аст, бинобар он: AB 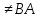 Агар дар вақти зарби матритсаҳо AB=BA бошад, он гоҳ ин матритсаҳоро матритсаҳои коммутативӣ меноманд.Мисол: A= 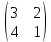 ва B= ва B=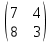 A A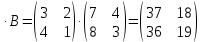 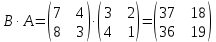 , яъне: AB=BA , яъне: AB=BA Ҳосили зарби табдилоти хаттии A-ро ба адади λA табдилотеро мефаҳмонад, ки он ба ҳар як вектори x вектори 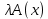 -ро мувофиқ мегузорад.Агар ба табдилоти хаттии A матритсаи -ро мувофиқ мегузорад.Агар ба табдилоти хаттии A матритсаи 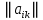 мувофиқ ояд, он гоҳ ба табдилоти λA матритсаи мувофиқ ояд, он гоҳ ба табдилоти λA матритсаи 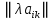 мувофиқ меояд. мувофиқ меояд.Якчанд мисолҳоро бо мафҳуми табдилоти хаттӣ ва амалҳо бо он татбиқ менамоем: Мисоли 1. Дар фазои сеченакаи 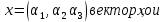 базиси базиси 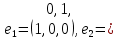 0), 0), 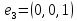 дода шудааст, матритсаи табдилоти хаттии дода шудааст, матритсаи табдилоти хаттии 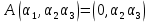 -ро дар ин базис ёбед. -ро дар ин базис ёбед.Ҳал: 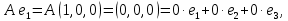 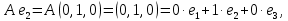 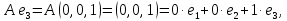 Аз ин ҷо матритсаи: 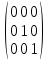 ҳосил мешавад. Мисоли 2. Дар фазои сеченакаи 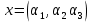 векторҳои базиси векторҳои базиси 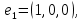 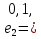 0), 0), 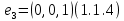 ва табдилоти хаттии 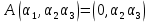 , , 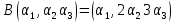 дода шудаанд. Матритсаҳои табдилоти дода шудаанд. Матритсаҳои табдилоти 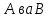 -ро дар базиси (1.1.4) ёбед. -ро дар базиси (1.1.4) ёбед.Ҳал: 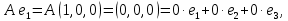 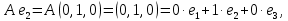 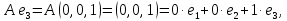 ва 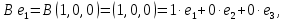 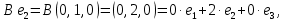 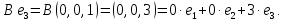 Ҳамин тавр: 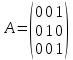 ва ва 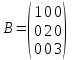 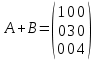 ва ва 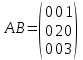 Аз ин ҷо: 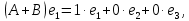 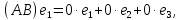 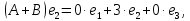 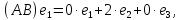 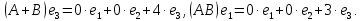 Табдилоти баръакс. Мафҳуми табдилоти баръакс ва мафҳуми матритсаи баръакс бо ҳамдигар алоқаманд мебошанд. Таърифи 4.Агар 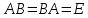 бошад, табдилоти бошад, табдилоти 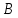 нисбат ба нисбат ба  баръакс номида мешавад, ки дар ин ҷо баръакс номида мешавад, ки дар ин ҷо 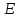 табдилоти воҳидӣ мебошад. табдилоти воҳидӣ мебошад.Табдилоти нисбат ба табдилоти  баръакс бо баръакс бо 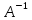 ишора карда мешавад.Барои ҳар як матритсае, ки шарти Det( ишора карда мешавад.Барои ҳар як матритсае, ки шарти Det(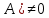 -ро қаноат мекунонад, матритсаи баръакси -ро қаноат мекунонад, матритсаи баръакси 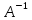 -ро муайян кардан мумкин аст, ки он шарти: -ро муайян кардан мумкин аст, ки он шарти: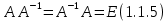 -ро қаноат мекунонад. Матритсаи 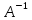 нисбат ба матритсаи нисбат ба матритсаи  баръакс номида мешавад. Системаи муодилаҳои хаттии бо баробарии матритсавии (1.1.5) баробарқувваро ҳал карда, матритсаи баръакс номида мешавад. Системаи муодилаҳои хаттии бо баробарии матритсавии (1.1.5) баробарқувваро ҳал карда, матритсаи 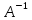 -ро ёфтан мумкин аст ва бе мушкилӣ санҷидан мумкин аст, ки матритсаи -ро ёфтан мумкин аст ва бе мушкилӣ санҷидан мумкин аст, ки матритсаи 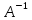 -и чунин тартиб додашуда шартҳои (1.1.5)-ро қаноат мекунонад. -и чунин тартиб додашуда шартҳои (1.1.5)-ро қаноат мекунонад.Азбаски дар базиси додашуда байни матритсаҳо ва табдилоти хаттӣ мувофиқати якқиматаи амали зарбро нигоҳдоранда мавҷуд аст,пас таърифи зеринро баён кардан мумкин аст: Барои он ки табдилоти  баръаксашро дошта бошад, зарур ва кифоя аст, ки муайянкунандаи матритсаи он дар ягон базис аз нол фарқ карданаш лозим аст, яъне бояд ранги баръаксашро дошта бошад, зарур ва кифоя аст, ки муайянкунандаи матритсаи он дар ягон базис аз нол фарқ карданаш лозим аст, яъне бояд ранги 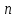 -ро дошта бошад. Табдилоте, ки табдилоти баръакс дорад, ғайримахсус номида мешавад. Табдилоти махсус табдилоти баръакс надорад. -ро дошта бошад. Табдилоте, ки табдилоти баръакс дорад, ғайримахсус номида мешавад. Табдилоти махсус табдилоти баръакс надорад.Мисол: Дар фазои сеченакаи 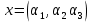 векторҳои базиси векторҳои базиси 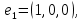 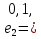 0), 0), 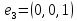 ва табдилоти хаттии ва табдилоти хаттии 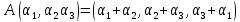 дода шудаанд. Табдилоти хаттии баръаксро ёбед. дода шудаанд. Табдилоти хаттии баръаксро ёбед.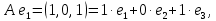 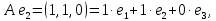 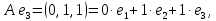 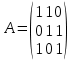 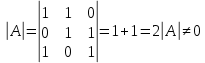 Аз сабабе, ки дар ин ҷо 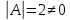 мебошад, мебошад, 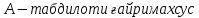 мебошад. Матритсаи ба матритсаи мебошад. Матритсаи ба матритсаи  баръаксро меёбем: баръаксро меёбем: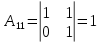 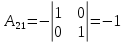 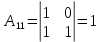 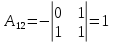 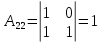 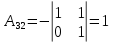 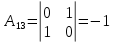 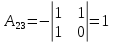 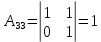 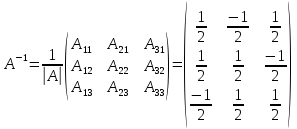 буда,матритсаи 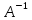 матритсаи дар базиси додашудаи табдилот мебошад. Ҳамин тавр: матритсаи дар базиси додашудаи табдилот мебошад. Ҳамин тавр: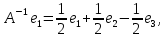 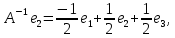 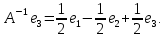 матритсаи баръакси табдилоти додашуда мебошад. §1.2 Векторҳои хос ва қиматҳои хоси табдилоти хаттӣ Барои омӯхтани векторҳои хос ва қиматҳои хоси табдилоти хаттӣ зерфазоҳои инвариантии якченака аҳамияти калон доранд. Тасаввур мекунем, ки 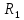 зерифазои якченакае бошад, ки бо вектори зерифазои якченакае бошад, ки бо вектори 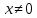 ба вуҷуд оварда шудааст. Барои инвариантӣ будани ба вуҷуд оварда шудааст. Барои инвариантӣ будани 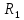 зарур ва кифоя аст, ки вектори зарур ва кифоя аст, ки вектори 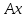 дар дар 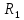 ҷойгир бошад, яъне нисбат ба вектори ҷойгир бошад, яъне нисбат ба вектори 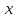 каратӣ бошад: каратӣ бошад: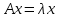 Таъриф. Вектори 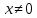 , ки баробарии , ки баробарии 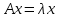 -ро қаноат мекунонад, вектори вектори хос ва адади ба он мувофиқи 𝜆 қимати хоси табдилоти хаттии -ро қаноат мекунонад, вектори вектори хос ва адади ба он мувофиқи 𝜆 қимати хоси табдилоти хаттии  ном дорад. ном дорад.Бинобар ин, агар 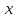 вектори хос бошад, векторҳои вектори хос бошад, векторҳои 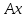 зерифазои инвариантии якченакаро ташкил мекунанд. зерифазои инвариантии якченакаро ташкил мекунанд.Теоремаи 1 Дар фазои комплексии 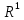 ҳар гуна табдилоти хаттии ҳар гуна табдилоти хаттии  ақаллан як вектори хос дорад. ақаллан як вектори хос дорад.Теоремаро исбот мекунем: Дар фазои 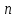 -ченакаи ихтиёрии -ченакаи ихтиёрии 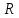 ягон базиси ягон базиси 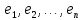 -ро интихоб мекунем.Дар ин базис ба табдилоти хаттии -ро интихоб мекунем.Дар ин базис ба табдилоти хаттии 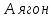 матритсаи матритсаи 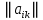 мувофиқ меояд. мувофиқ меояд.Фарз мекунем, ки: 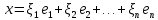 вектори ихтиёрии вектори ихтиёрии 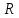 ва ва 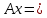 ( (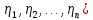 бошад, он гоҳ координатаҳои бошад, он гоҳ координатаҳои  -и вектори -и вектори 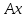 бо формулаҳои зерин ифода карда мешаванд: бо формулаҳои зерин ифода карда мешаванд: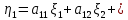 ... ... 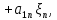 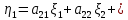 ... ... 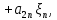  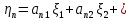 ... ...  Дар ҳолате, ки вектори додашуда хос аст, яъне баробарии 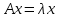 иҷро мегардад, ба таври зерин навишта мешавад: иҷро мегардад, ба таври зерин навишта мешавад: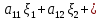 ... ... 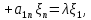 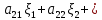 ... ... 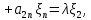 . . . . . . . . . . . . . . . . . 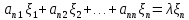 ё ин ки 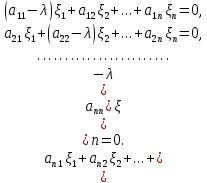 Ҳамин тариқ, барои исбот кардани теоремаи додашуда исбот кардан зарур аст, ки адади 𝜆 ва ададҳои 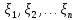 -и нобаробари нул вуҷуд доранд, ки системаи (1.2.1)-ро қаноат мекунонанд. -и нобаробари нул вуҷуд доранд, ки системаи (1.2.1)-ро қаноат мекунонанд.Системаи якҷинсаи дар боло овардашуда, танҳо дар ҳолате ҳалли ғайринулии худро дорад, ки муайянкунандаи он баробари нул бошад: 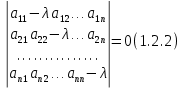 Дар натиҷаи табдилдиҳиҳо мо нисбат ба 𝜆 муодилаи дараҷаи 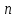 -умро ҳосил намудем. Ин муодила ҳадди ақал як решаи -умро ҳосил намудем. Ин муодила ҳадди ақал як решаи 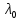 (яъне комплексӣ) дорад. (яъне комплексӣ) дорад.Дар системаи якҷинсаи (1.2.1) ба ҷои 𝜆 решаи 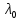 –ро гузошта, системаи муодилаҳои хаттии якҷинсаро ҳосил мекунем, ки муайянкунандаи он ба нул баробар мебошад ва бинобар ин ҳалли ғайринулии –ро гузошта, системаи муодилаҳои хаттии якҷинсаро ҳосил мекунем, ки муайянкунандаи он ба нул баробар мебошад ва бинобар ин ҳалли ғайринулии 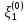 , , 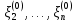 -ро дорад. Он гоҳ вектори -ро дорад. Он гоҳ вектори 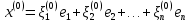 вектори хос ва 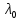 –қимати хоси табдилоти хаттии –қимати хоси табдилоти хаттии  мешавад, барои он ки мешавад, барои он ки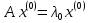 аст. Теоремаро исбот кардем. Бисёраъзогии тарафи чапи муодилаи (1.2.2)-ро бисёраъзогии характеристикии матритсаи табдилоти  ва худи муодилаи (1.2.2)-ро муодилаи характеристикӣ ё муодилаи қадимии ин матритса меноманд. Ҳангоми исботи теорема нишон додем, ки решаҳои бисёраъзогии характеристикӣ қиматҳои хоси табдилоти хаттии ва худи муодилаи (1.2.2)-ро муодилаи характеристикӣ ё муодилаи қадимии ин матритса меноманд. Ҳангоми исботи теорема нишон додем, ки решаҳои бисёраъзогии характеристикӣ қиматҳои хоси табдилоти хаттии  , ва баръакс қиматҳои хоси табдилоти хаттии , ва баръакс қиматҳои хоси табдилоти хаттии  решаҳои бисёраъзогии характеристикӣ мебошанд. решаҳои бисёраъзогии характеристикӣ мебошанд.Дар байни табдилоти хаттӣ он табдилоте, ки 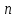 вектори хоси хаттии новобаста дорад, соддатарин мебошад. вектори хоси хаттии новобаста дорад, соддатарин мебошад.Тасаввур мекунем, ки  ҳамин гуна табдилот буда, ҳамин гуна табдилот буда, 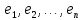 векторҳои хоси хаттӣ новобастаи он мебошанд, яъне векторҳои хоси хаттӣ новобастаи он мебошанд, яъне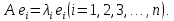 Векторҳои 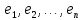 -ро ҳамчун базиси R қабул мекунем. Баробариҳои -ро ҳамчун базиси R қабул мекунем. Баробариҳои 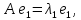 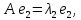 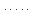 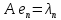 ҳаминро ифода мекунад, ки намуди матритсаи табдилоти  дар ин базис чунин мебошад: дар ин базис чунин мебошад: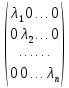 Теоремаи 2. Агар табдилоти хаттии 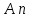 вектори хоси хаттӣ новобаста дошта бошад, онҳоро ҳамчун базисе интихоб намуда, мо матритсаи табдилоти -ро ба шакли диагоналӣ меоварем. Баръакс, агар дар ягон базис матритсаи табдилоти диагоналӣ бошад, он гоҳ ҳамаи векторҳои ин базис векторҳои хос мебошанд. вектори хоси хаттӣ новобаста дошта бошад, онҳоро ҳамчун базисе интихоб намуда, мо матритсаи табдилоти -ро ба шакли диагоналӣ меоварем. Баръакс, агар дар ягон базис матритсаи табдилоти диагоналӣ бошад, он гоҳ ҳамаи векторҳои ин базис векторҳои хос мебошанд.Мо бояд инро дар хотир нигоҳ дорем, ки: Агар бисёраъзогии характеристикии табдилоти  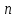 решаи гуногун дошта бошад, он гоҳ матритсаи табдилоти решаи гуногун дошта бошад, он гоҳ матритсаи табдилоти  -ро ба шакли диагоналӣ овардан мумкин аст. -ро ба шакли диагоналӣ овардан мумкин аст.Дар табдилоти хаттӣ ба ҳар як решаи 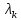 -и муодилаи характеристикӣ ақаллан як вектори хос мувофиқат мекунад. Барои он ки решаҳои муодилаи характеристикии ба ин векторҳо мувофиқоянда гуногун мебошанд, пас -и муодилаи характеристикӣ ақаллан як вектори хос мувофиқат мекунад. Барои он ки решаҳои муодилаи характеристикии ба ин векторҳо мувофиқоянда гуногун мебошанд, пас 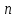 вектори хоси новобастаи вектори хоси новобастаи 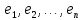 вуҷуд дорад. Агар векторҳои вуҷуд дорад. Агар векторҳои 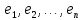 -ро ҳамчун базис қабул кунем, он гоҳ матритсаи табдилоти -ро ҳамчун базис қабул кунем, он гоҳ матритсаи табдилоти  диагоналӣ мешавад. диагоналӣ мешавад.Оиди ҳалли қимати хос ва вектори хоси табдилоти хаттӣ якчанд мисолҳоро тадқиқ менамоем: Мисоли 1.Бисёраъзогии характеристикиро тартиб диҳед: а 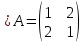 б) б)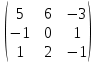 в) в)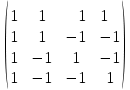 Ҳал: а) 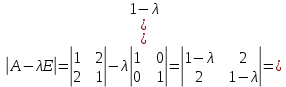 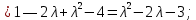 б) 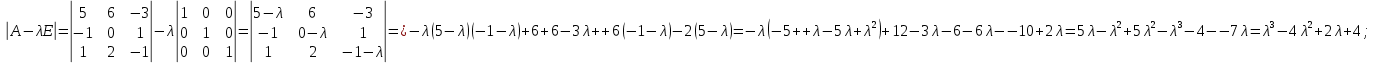 в) 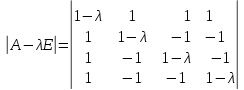 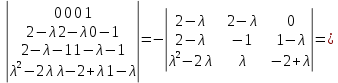 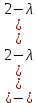 . .Мисоли 2. Аз рӯи базиси табдилоти хаттӣ матритсаи 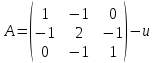 зерин тартиб дода шудааст. Қимати хос ва вектори хоси табдилоти хаттиро ёбед. зерин тартиб дода шудааст. Қимати хос ва вектори хоси табдилоти хаттиро ёбед.Ҳал: Муодилаи характеристикиро тартиб медиҳем. 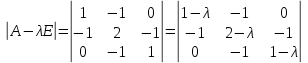 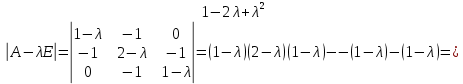 )( )(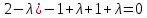 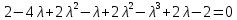 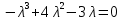 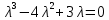 𝜆( 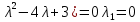 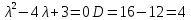 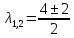 ; ;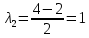 ; ; 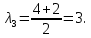 Ҳалҳои муодилаи дода шуда ба 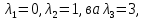 баробар аст.Акнун қимати баробар аст.Акнун қимати 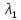 -ро ба матритса гузошта, ифодаи зеринро щосил мекунем: -ро ба матритса гузошта, ифодаи зеринро щосил мекунем:а) 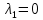 ( (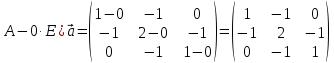 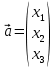 ( 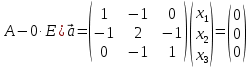 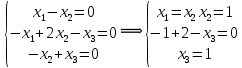 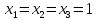 қимати хоси қимати хоси 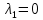 ва вектори хос ва вектори хос 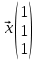 мебошад. мебошад.б) 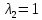 ( (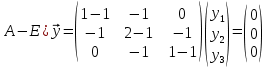 ( 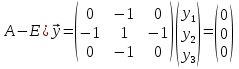 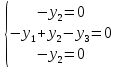 ⟹ ⟹ 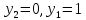 , , 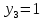 -қимати хос ва -қимати хос ва 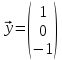 вектори хос мебошад. Акнун қимати хоси 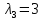 -ро ба матритса гузошта, ифодаҳои зеринро ҳосил менамоем: -ро ба матритса гузошта, ифодаҳои зеринро ҳосил менамоем: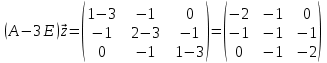 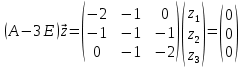 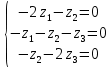 ⟹ ⟹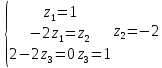 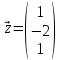 Векторҳои 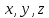 -ро ҳосил кардем, ки онҳо новобастаи хаттӣ аст, азбаски қиматҳои векторҳои ҳақиқӣ ва ҳархела аст. -ро ҳосил кардем, ки онҳо новобастаи хаттӣ аст, азбаски қиматҳои векторҳои ҳақиқӣ ва ҳархела аст.Мисоли 3. Аз рӯи базиси табдилоти хаттӣ матритсаи 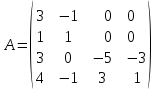 дода шудааст.Қимати хос ва вектори хоси табдилоти хаттиро ёбед. дода шудааст.Қимати хос ва вектори хоси табдилоти хаттиро ёбед.Ҳал: ∆ 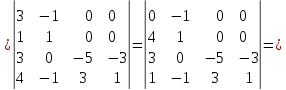 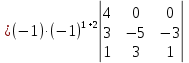 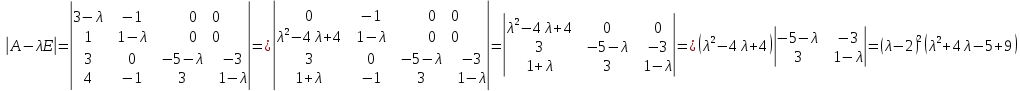 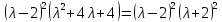 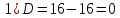 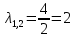 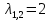 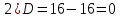 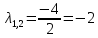 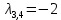 Қиматҳои хоси табдилоти хаттӣ 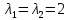 ва ва 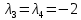 мебошанд. Векторҳои хоси мебошанд. Векторҳои хоси 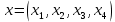 -ро ҷустуҷӯ менамоем: -ро ҷустуҷӯ менамоем: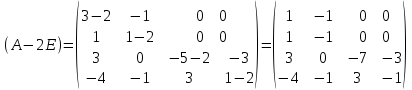 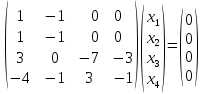 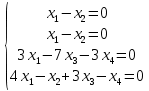 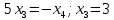 Системаи муодилаи хаттии якҷинсаро бо системаи муодилаи хаттии баробарқувва иваз мекунем: 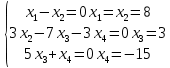 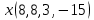 ( 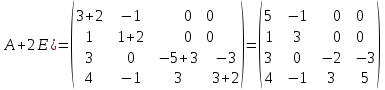 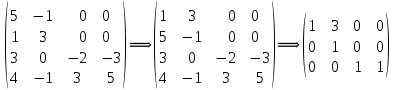 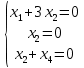 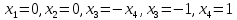 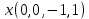 Боби якум ба омӯзиши табдилотҳои хаттӣ, амалҳо бо онҳо, зерфазоҳои инвариантӣ, вектори хос ва қиматҳои хоси табдилоти хаттӣ бахшида шудааст. Дар ин боб амалҳо бо табдилотҳои хаттӣ, хосиятҳои асосии табдилотҳои хаттӣ, табдилотҳои баръаксӣ ва ҳисобкардани табдилотҳои баръаксӣ, алоқаи байни матритсаҳои табдилоти хаттӣ дар базисҳои гуногун, векторҳои хос ва қиматҳои хоси табдилоти хаттӣ ва тартиб додани муодилаи характеристикии векторҳои хос омӯхта шудааст. |
