практика математика замфиреску. Цель занятия формирование умений решать текстовые задачи применять математические методы для решения профессиональных задач закрепление навыков решения простейших статистических задач
 Скачать 1.43 Mb. Скачать 1.43 Mb.
|
|
Практическое занятие 2 Цель занятия: формирование умений решать текстовые задачи; применять математические методы для решения профессиональных задач; закрепление навыков решения простейших статистических задач; закрепление навыков применять правила приближенных вычислений; закрепление навыков работы с основными свойствами геометрических фигур на плоскости и в пространстве. Задание 1. (Максимальное количество баллов – 3 балла) Таблица – «Виды моделирования при решении текстовых задач» В таблице «Виды моделирования при решении текстовых задач» заполните позицию «Необходимо определить» в графе «Интерпретация модели».
Задание 2. (Максимальное количество баллов – 3 балла) Используя диаграммы Эйлера-Венна решить задачу. При выборе кружков для детей оказалось, что 60% родителей желают, чтобы их ребенок посещал кружок рисования, 50% предпочли занятия по гимнастике, 50% отметили, что выбрали бы занятия музыкой. При этом 30% родителей предпочитают, чтобы их дети посещали занятия и по рисованию, и по гимнастике, 20% – сделали выбор в пользу занятий по гимнастике и музыке, а 40% родителей – пожелали бы, чтобы ребенок рисовал и занимался хоровым пением, и только 10% из них выразили свое мнение за посещение детьми всех кружков. Определите процентное соотношение родителей, которые: 1) не желают водить детей в кружки: 100-70-10=20 % 2) выбрали не менее двух кружков: 30+20+10+10=70% Задание 3 (максимальное количество баллов – 5 баллов) При измерении получены данные:
Выполните задания с учетом исходных данных, подробно описывая ход решения. a) Построить статистический ряд распределения частот. b) Построить полигон распределения. c) Вычислить выборочную среднюю, дисперсию, моду, медиану. d) Построить выборочную функцию распределения. Построим дискретный вариационный ряд. Для этого отсортируем ряд по возрастанию и подсчитаем количество повторения для каждого элемента ряда.
Таблица для расчета показателей.
Для оценки ряда распределения найдем следующие показатели: Показатели центра распределения. Средняя взвешенная (выборочная средняя) 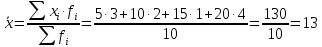 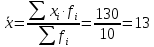 Мода. Мода - наиболее часто встречающееся значение признака у единиц данной совокупности. Максимальное значение повторений при x = 20 (f = 4). Следовательно, мода равна 20. Медиана. Медианой (Me) называется значение признака, приходящееся на середину ранжированной (упорядоченной) совокупности. Находим xi, при котором накопленная частота S будет больше ∑{f/2} = 6. Это значение xi = . Таким образом, медиана равна . Медиана служит хорошей характеристикой при ассиметричном распределении данных, т.к. даже при наличии "выбросов" данных, медиана более устойчива к воздействию отклоняющихся данных. В симметричных рядах распределения значение моды и медианы совпадают со средней величиной (xср=Me=Mo), а в умеренно асимметричных они соотносятся таким образом: 3(xср-Me) ≈ xср-Mo Показатели вариации. Абсолютные показатели вариации. Размах вариации - разность между максимальным и минимальным значениями признака первичного ряда. R = xmax - xmin = 20 - 5 = 15 Среднее линейное отклонение - вычисляют для того, чтобы учесть различия всех единиц исследуемой совокупности. 𝑑 = 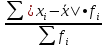 = =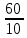 = 6 = 6Каждое значение ряда отличается от другого в среднем на 6 Дисперсия - характеризует меру разброса около ее среднего значения (мера рассеивания, т.е. отклонения от среднего). 𝐷 = 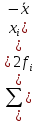 = =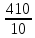 = 41 = 41Среднее квадратическое отклонение. 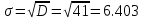 Каждое значение ряда отличается от среднего значения 13 в среднем на 6.403 Относительные показатели вариации. К относительным показателям вариации относят: коэффициент осцилляции, линейный коэффициент вариации, относительное линейное отклонение. Коэффициент вариации - мера относительного разброса значений совокупности: показывает, какую долю среднего значения этой величины составляет ее средний разброс.  Поскольку v>30% ,но v<70%, то вариация умеренная. Линейный коэффициент вариации или Относительное линейное отклонение - характеризует долю усредненного значения признака абсолютных отклонений от средней величины. 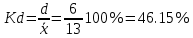 Коэффициент осцилляции - отражает относительную колеблемость крайних значений признака вокруг средней. 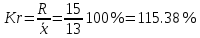 Выводы: Каждое значение ряда отличается от среднего значения 13 в среднем на 6.403. Поскольку коэффициент вариации находится в пределах [30%; 70%], то вариация умеренная 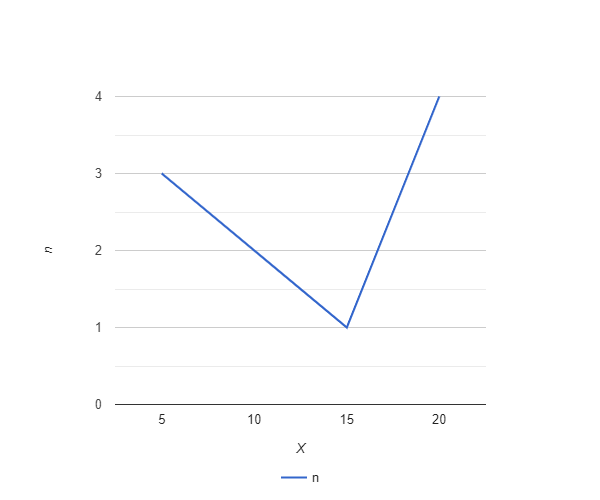 + +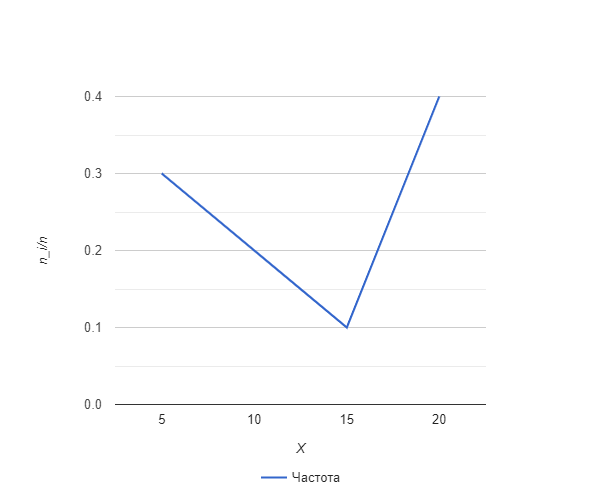 Задание 4 (максимальное количество баллов - 4 балла) Решите примеры, связанные с погрешностями, подробно описывая ход решения. a) Округлить число 4,45575250 до шести, пяти, четырех, трех, двух и одного десятичных знаков; до целого числа. b) Число 12,75 определено с относительной погрешностью 0,3, %. Найдите абсолютную погрешность округления. c) Определите верные и сомнительные цифры числа 13,27 ± 0,03. a) 4,45575250 до шести знаков = 4,455753 4,45575250 до пяти знаков = 4,45575 4,45575250 до четырёх знаков = 4,4558 4,45575250 до трех знаков = 4,456 4,45575250 до двух знаков = 4,46 4,45575250 до одного знака = 4,5 4,45575250 до целого числа = 4 b) Округляя число 12,75 получаем 12,8. Прибавляем 1 к десятым, потому что сотые больше 5. Абсолютная погрешность равна модулю разницы между точным и округленным числом, 12,8 – 12,75 = 0,05 Относительная погрешность равна абсолютной, деленной на приближенное значение, выраженное в процентах, 0,05 / 12,8 * 100% = 0,003% c) Определение: «Цифра называется верной, если граница абсолютной погрешности данного приближенного значения числа не больше единицы того разряда, в котором записана эта цифра. В противном случае цифра называется сомнительной». х = 13,75 ± 0,03 0,03 - граница абсолютной погрешности Единица последнего разряда - 0,01 (сотые) 0,03 > 0,01 значит цифра 5 - сомнительная 0,03 < 0, 1 - значит цифра 2 - верная Если в записи приближенного значения числа какая-то цифра – верная, то и все предшествующие ей цифры так же являются верными. Значит 3; 1 - также верные цифры В записи приближенного значения числа сохраняют только верные цифры, а сомнительные цифры округляют, значит х = 13,3 Задание 5 (максимальное количество баллов – 3 балла) Решите задачу, подробно описывая ход рассуждений. Решение сопроводите графическим отображением. На стороне AC треугольника ABC отмечена точка D так, что AD=3см, DC=10см. Площадь треугольника ABC равна 39 см2. Найдите площадь треугольника ABD. 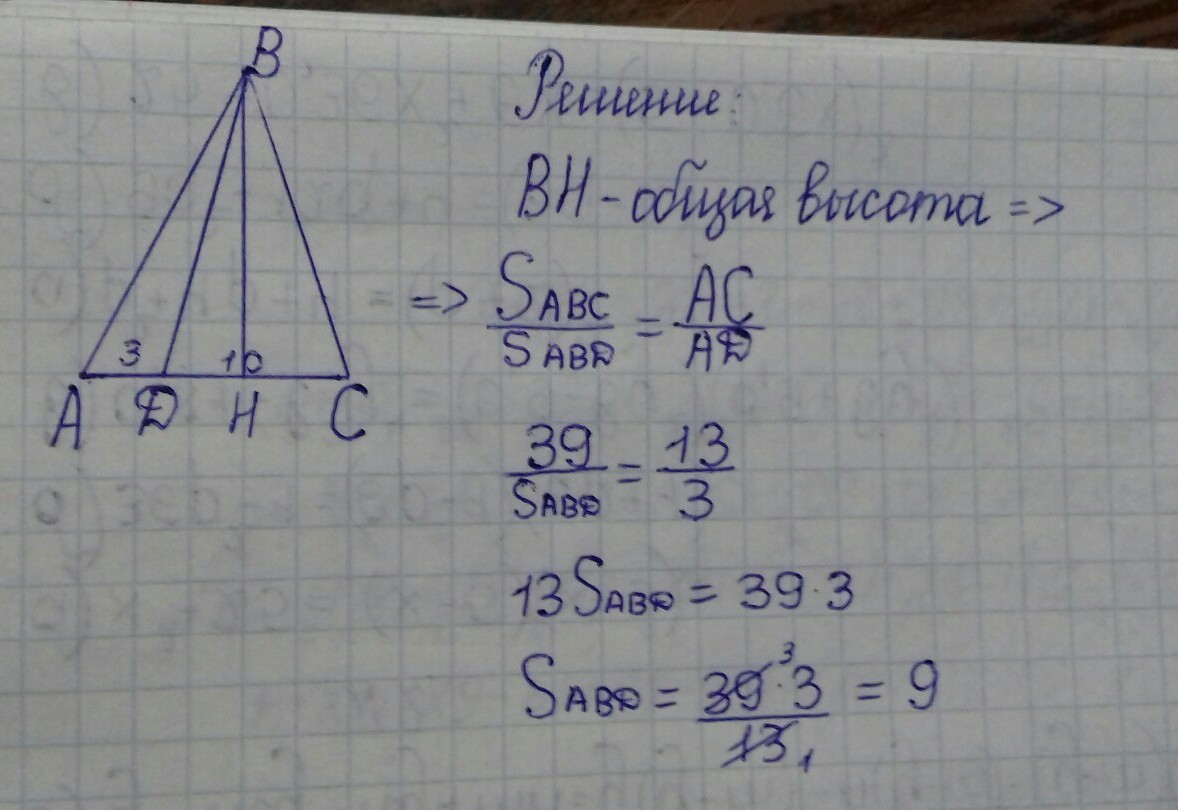 BH – общая высота, следовательно SABC/SABD = AC/AD 39/SABD = 13/3 13 SABD = 39*3 SABD = 39*3/13 = 9 Ответ: 9 см2. Задание 6 (максимальное количество баллов – 4 балла) Решите задачу, подробно описывая ход рассуждений. Решение сопроводите графическим отображением. Биссектриса угла A параллелограмма ABCD пересекает его сторону BC в точке F. Найдите площадь параллелограмма ABCD, если BF=4 см, FC=2 см, а угол ABC равен 1500. Дано: параллелограмм ABCD, BF=4 см, FC=2 см, ∠ABC=1500. Найти: S параллелограмма ABCD Решение: Накрест лежащие углы BFA и FAD равны, AF — биссектриса ∠BAD, следовательно, ∠ BFA и ∠ FAD = ∠ BAF Значит, треугольник BFA равнобедренный и AB=BF=4 По формуле площади параллелограмма находим: S=4*7*1/2=14 см2 Ответ: 14 см2 Задание 7 (максимальное количество баллов – 3 балла) Решите задачу, подробно описывая ход рассуждений. Решение сопроводите графическим отображением. Найдите площадь поверхности прямой призмы, в основании которой лежит ромб с диагоналями, равными 6см и 8см, а боковое ребро призмы равно 12см. 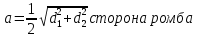 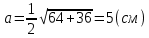 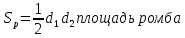 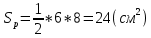 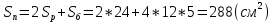 Ответ: 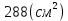 Рисунки к задачам: 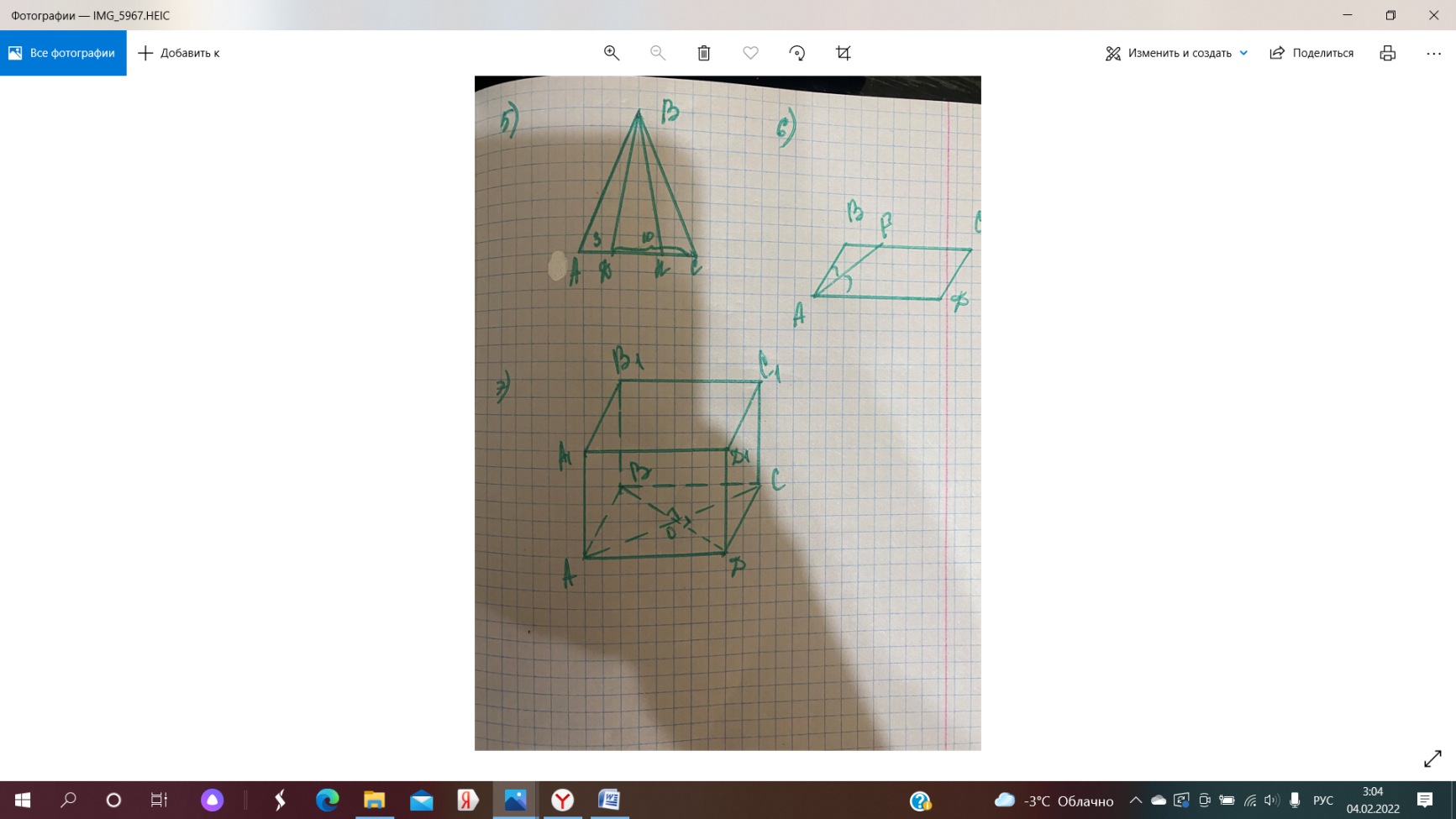 |

