Инвестиционный менеджмент. Текст. Цели и задачи дисциплины, ее место и роль в учебном процессе

• Название: Цели и задачи дисциплины, ее место и роль в учебном процессе
• Анкор: Инвестиционный менеджмент
• Дата: 10.02.2023
• Размер: 1.45 Mb.
• Имя файла: Текст.docx
• Тип: Документы; #930638
• страница: 4 из 9

Тема 3. Методы оптимизации инвестиционного портфеля

 

Цель данной темы– изучение методики формирования инвестиционного портфеля в соответствии теорией Марковица и в соответствии с теорией Шарпа. Сравнение теорий Марковица и Шарпа.

 

Задачи изучения темы:

     изучить основные допущения теории Марковица;

     изучить методику расчета средней ожидаемой доходности и риска отдельной ценной бумаги и инвестиционного портфеля;

     определить понятие эффективного портфеля;

     определить сущность оптимального портфеля;

     построить границу эффективных портфелей в виде общей схемы;

     изучить нахождение оптимального портфеля в соответствии с теорией Марковица;

     изучить применение метода линейного регрессионного анализа в рамках теории Шарпа;

     определить сущность коэффициентов α и β;

     изучить нахождение оптимального портфеля методом Шарпа.

 

Вопросы темы:

1.  Основные положения модели Марковица.

2.  Оптимизация инвестиционного портфеля в соответствии с теорией Шарпа.

 

Изучив данную тему, студент должен:

знать:

     основные положения модели Г. Марковица и У. Шарпа;

     содержание эффективного портфеля;

     содержание оптимального портфеля;

     метод линейного регрессионного анализа;

     определение доходности и риска портфеля с помощью коэффициентов α и β;

     нахождение оптимального портфеля по методу У. Шарпа.

 

уметь:

     определять ожидаемую доходность и риск отдельной акции портфеля;

     определять ожидаемую доходность и риск портфеля;

     строить границу эффективного портфеля;

     находить оптимальный портфель из эффективных портфелей;

     применять регрессионный анализ при оценке оптимального портфеля;

     вычислять дисперсию ошибок;

     находить ожидаемую доходность, дисперсию отдельной акции и портфеля с использованием коэффициентов α и β;

     вычислять параметры оптимального портфеля по теории У. Шарпа.

 

Вопрос 1. Основные положения модели Марковица.

 

В 1952 году американский экономист Гарри М. Марковиц (Harry M. Markowitz) опубликовал статью «Portfolio Selection» в журнале «Journal of Finance», которая послужила отправным моментом для развития целого направления экономической науки – разработки теории инвестиционного портфеля. Подход Марковица к инвестиционному процессу, как и в любой теории, включает ряд научных абстракций и допущений.

Основные положения модели Г. Марковица. Модель Марковица основывается на ряде допущений.

Допущение 1: инвестирование в портфель акций осуществляется на один шаг расчета (один холдинговый период). Иными словами, в определенный момент t₀ портфель формируется, не трансформируется в течение холдингового периода, а затем по его окончании в момент t₁ портфель ликвидируется.

Допущение 2: Рынок ценных бумаг (РЦБ) является эффективным.

Согласно теории инвестиционного портфеля, единственным основанием для принятия инвестиционного решения на РЦБ служит имеющаяся в распоряжении инвестора информация о событиях, которые произойдут на рынке ценных бумаг за холдинговый период. Совместные действия инвесторов, вызванные этой информацией, отразятся в спросе на акции корпорации и их предложении, что повлечет изменения их цен. Эффективность рынка ценных бумаг определяется тем, сколь быстро и адекватно эта информация трансформируется в изменение цен на финансовые средства.

Эффективным считается такой рынок ценных бумаг, где их цены адекватно отражают всю поступающую информацию, и цены финансовых средств (акций) приводятся в соответствие с вновь поступающей информацией немедленно, в течение первых же торгов после того, как она стала доступной широкой публике.

К достаточным условиям существования эффективного рынка ценных бумаг относят следующие:

1)      Сделки с ценными бумагами происходят без трансакционных издержек (комиссионные брокеров, спрэд дилеров и т.п.).

2)      Информация о рынке ценных бумаг доступна любому инвестору.

3)      Все инвесторы имеют однородные (гомогенные) ожидания, то есть одинаково оценивают содержание информации о будущих ценах на рынках каждой ценной бумаги.

4)      Ни один из инвесторов не в состоянии оказывать воздействие на цены любых финансовых средств.

 

Допущение 3: информация, влияющая на цены акций, случайна во времени, поэтому цены акций, а значит и их доходности, имеют также случайный характер. Данные обстоятельства позволяют применять к исследованию рынка ценных бумаг аппарат теории вероятностей.

Допущение 4: Доходность акции за будущий холдинговый период с определенной вероятностью будет равняться средней арифметической величине  доходностей  этой акции, вычисленных за прошлые шаги расчета. Эту среднюю арифметическую величину называют ожидаемой доходностью   акции.

Формируя портфель ценных бумаг в начальный момент времени t₀, инвестор должен учитывать доходность ценных бумаг портфеля за будущий холдинговый период. Очевидно, что вычислить эту доходность невозможно, так как в момент t₀ инвестору не известны цены акций в конце холдингового периода в момент t₁. Значит, доходность ценных бумаг портфеля за будущий холдинговый период можно только оценить, имея в виду допущение 3 о случайном характере изменения цен и доходностей акций. Существуют два подхода к оценке значений случайных величин  субъективный и объективный.

При использовании субъективного подхода инвестор, прежде всего, должен определить возможные сценарии развития экономической ситуации в течение будущего холдингового периода, оценить вероятность каждого результата и ожидаемую при этом отдачу ценной бумаги. В качестве примера в таблице 4 приведены данные о субъективном распределении вероятностей будущей отдачи ценной бумаги X.

 

Таблица 4.

 

Субъективное распределение вероятностей отдачи ценной бумаги Х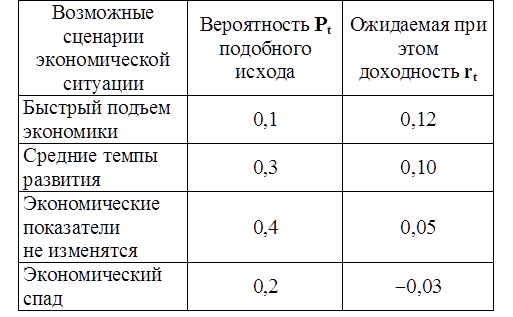

 



 

После этого обычно находят среднюю арифметическую величину А(r_t) вычисленных значений r_t:

 

среднее арифметическое

 

А(r_t ) =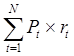 

 

где

N – количество шагов расчета, в течение которых велись наблюдения. В рассматриваемом примере: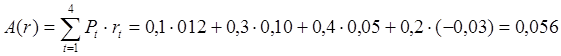

 



 

С учетом этого значения, можно полагать, что применительно к ценной бумаге Х ее доходность за будущий шаг расчета с определенной вероятностью составит 5,6% (0,056).

Субъективный подход не находит широкого применения, поскольку для обычного инвестора очень трудно сделать оценку вероятностей экономических сценариев и ожидаемой при этом доходности.

Поэтому в модели Г. Марковица используется объективный подход. В его основе лежит предположение о том, что распределение вероятностей будущих (ожидаемых) величин практически совпадает с распределением вероятностей уже наблюдавшихся, фактических, исторических величин. Значит, чтобы получить представление о распределении случайной величины r в будущем достаточно построить распределение этих величин за какой-то промежуток времени в прошлом. Если проводится оценка доходности выбранной акции за будущий холдинговый период, то используют следующий алгоритм:

1)      Задают длительность будущего холдингового периода (например, 1 месяц).

2)      Выбирают в прошлом периоде времени N шагов расчета, равных по длительности будущему холдинговому периоду.

3)      Поскольку информация о ценах акции доступна, то выявляют цены акций в начале и в конце каждого шага расчета.

4)      По формуле: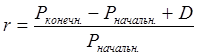

 



 

где

P_{конечн.} – цена акции в конце шага расчета;

Р_{начальн.} – цена акции в начале шага расчета;

D – полученный за шаг расчета дивиденд) находят N значений доходности акции r_t за каждый шаг расчета.

 

5)      Находят среднюю арифметическую величину 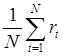  вычисленных доходностей  . При этом следует учитывать, что в случае объективного способа все вычисленные значения  равновероятны и вероятность каждого значения   одна и та же: P_t=1/N. Поэтому формула для вычисления  примет вид: 

 

 = 

 

С учетом изложенного алгоритма, повторим еще раз допущение 4 модели Марковица с некоторыми дополнениями: доходность акции за будущий холдинговый период с определенной вероятностью будет равняться средней арифметической величине 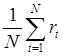 доходностей  этой акции, вычисленных за прошлые шаги расчета. Эту среднюю арифметическую величину называют ожидаемой доходностью   акции, то есть:

 

 = 

 

Чтобы в дальнейшем иметь возможность оперировать конкретными данными, рассмотрим три условные фирмы «А», «В» и «С», доходности акций которых за 10 шагов расчета приведены в таблице 5:

 

Таблица 5.

 

Значение доходности акций трех фирм за 10 шагов расчета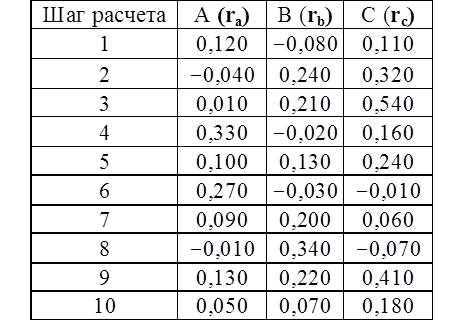

 



 

Вычислим ожидаемые (средние арифметические) доходности акций наших трех фирм: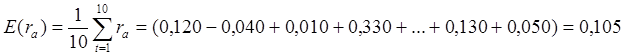

 

 

 

или 10,5%.

 

Аналогичные вычисления для акций «Веги» и «Сириуса» дают:

 

 = 0,128, или 12,8%;   = 0,194, или 19,4%.

 

Измерение риска отдельной акции портфеля. Доходность оцениваемой акции за будущий холдинговый период равняется ожидаемой доходности 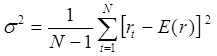  с определенной долей вероятности, значит, существует риск того, что реализованная доходность акции, вычисленная по окончании будущего холдингового периода, будет отличаться от ожидаемой величины  . Мерой такого риска выступает дисперсия  доходности акции, вычисляемая как ожидаемая (средняя арифметическая) величина квадратов отклонения величин   от ожидаемой доходности акции  :

 



 

Поскольку ожидаемая доходность акции   выражается в процентах, а размерность дисперсии – квадрат процента, то для адекватного сравнения доходности и риска акции используют в качестве меры риска величину стандартного отклонения :

 



 

Вычислим дисперсии и стандартные отклонения доходностей акций наших трех фирм: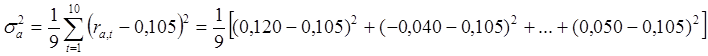

 

 =0,014

 

= = 0,118.

 

Аналогичные вычисления для двух других акций дают:

 

 = 0,019 и  = 0,138;  = 0,036 и  = 0,189

 

При оценке инвестиционной привлекательности акций следует предпочесть ту из них, которая обеспечивает более высокую ожидаемую доходность и меньший уровень риска. Однако на практике более доходные акции часто имеют и более высокий уровень риска. В этом случае инвестиционный выбор можно сделать с использованиемкоэффициента отклонения CV: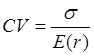

 

,

 

показывающего, какая доля риска приходится на один процент ожидаемой доходности. Предпочесть следует ту акцию, которая имеет наименьшее значение CV.

 

Для наших акций получаются следующие значения: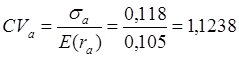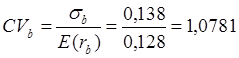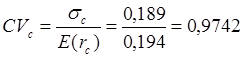

 



 



 



 

То есть предпочесть следует акцию С.

 

Измерение доходности и риска портфеля. Чтобы найти доходность и риск всего портфеля инвестору, прежде всего, необходимо определить, какую долю из имеющейся у него на момент tсуммы денег S_{начальн.} он направит на приобретение той или иной акции портфеля. Предположим, что инвестор располагает суммой S_{начальн.} =10 тыс. рублей и решает сумму S_a направить на приобретение акции А, а сумму S_b – на покупку акции В. Принято долю: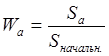

 

,

 

направленную на приобретение акций «А», называть весомакции А в портфеле. Соответственно 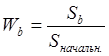 является весом акций «В» в портфеле. Тогда для любой i-ой акции портфеля ее вес: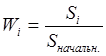

 

.

 

Очевидно, что если в портфель включено n акций, то сумма весов всех акций портфеля должна равняться единице: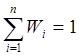

 



 

Доходность портфеля. Пусть в портфель объединяются n акций. На инвестиционной терминологии данная фраза означает, что в портфель включены акции n эмитентов. Так, если в формируемый портфель будет включено 10 акций фирмы «А», 20 акций «В» и 30 акций «С», то считается, что такой портфель содержит 3 акции. Алгебраически под ожидаемой доходностью портфеля понимается средневзвешенное значение ожидаемых величин доходности акций, входящих в портфель: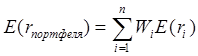

 

,

 

где

  ожидаемая доходность портфеля;

 – вес i-ой акции в портфеле;

  ожидаемая доходность i-ой акции;

n – число акций в портфеле.

 

Если инвестор решит сформировать портфель из акций трех компаний и разделить начальный капитал между ними в пропорции: W_a=0,1; W_b=0,35; W_c=0,55, то:

 

E(r_a+b+c)=0,1×0,105+0,35×0,128+0,55×0,194=0,162