Задача. Задача 4. Четвертая метод монтекарло. Цепи маркова

• Название: Четвертая метод монтекарло. Цепи маркова
• Анкор: Задача
• Дата: 13.01.2022
• Размер: 301 Kb.
• Имя файла: Задача 4.doc
• Тип: Документы; #330450
• страница: 3 из 3

Глава двадцать вторая

ПЕРВОНАЧАЛЬНЫЕ СВЕДЕНИЯ О ЦЕПЯХ МАРКОВА

§ 1. Цепь Маркова

Цепью Маркова называют последовательность испытаний, в каждом из которых появляется только одно из k несовместных событий A₁, A₂,…,A_k полной группы, причем условная вероятность р_ij(s) того, что в s-м испы­тании наступит событие Aj(j=1,2, ...,n), при усло­вии, что в (s—1)-м испытании наступило событие A_i(i=1, 2, ...,n), не зависит от результатов предшест­вующих испытаний.

Например, если последовательность испытаний обра­зует цепь Маркова и полная группа состоит из четырех несовместных событий A₁,A₂,A₃,A₄, причем известно, что в шестом испытании появилось событие A₂ то условная вероятность того, что в седьмом испытании насту­пит событие A₄, не зависит от того, какие события поя­вились в первом, втором, .... пятом испытаниях.

Заметим, что независимые испытания являются част­ным случаем цепи Маркова. Действительно, если испы­тания независимы, от появление некоторого определенного события в любом испытании не зависит от результатов ранее произведенных испытаний. Отсюда следует, что понятие цепи Маркова является обобщением понятия независимых испытаний.

Далее используется терминология, которая принята при изложении цепей Маркова. Пусть некоторая система в каждый момент времени находится в одном из k состоя­ний: первом, втором, ..., k-м. В отдельные моменты времени в результате испытания состояние системы изме­няется, т.е. система переходит из одного состояния, например i, в другое, например j. В частности, после испытания система может остаться в том же состоянии («перейти» из состояния i в состояние j=i.

Таким образом, события называют состояниями си­стемы, а испытания—изменениями ее состояний.

Дадим теперь определение цепи Маркова, используя новую терминологию.

Цепью Маркова называют последовательность испы­таний, в каждом из которых система принимает только одно из k состояний полной группы, причем условная вероятность р_ij(s) того, что в s-м испытании система будет находиться в состоянии j, при условии, что после (s—1)-го испытания она находилась в состоянии i, не зависит от результатов остальных, ранее произведенных испытаний.

Цепью Маркова с дискретным временем называют цепь, изменение состояний которой' происходит в опре­деленные фиксированные моменты времени.

Цепью Маркова с непрерывным временем называют цепь, изменение состояний которой происходит в любые случайные возможные моменты времени.
§ 2. Однородная цепь Маркова.

Переходные вероятности. Матрица перехода

Однородной называют цепь Маркова, если услов­ная вероятность р_ij(s) (перехода из состояния i в состоя­ние j) не зависит от номера испытания. Поэтому вместо р_ij(s) пишут просто р_ij.

Пример. Случайное блуждание. Пусть на прямой Ох в точке с целочисленной координатой х=п находится материальная частица. В определенные моменты времени ,t₁,t₂,t₃, … частица испытывает толчки. Под действием толчка частица с вероятностью р смещается на единицу вправо и с вероятностью 1—р —на единицу влево. Ясно, что положение (координата) частицы после толчка зави­сит от того, где находилась частица после непосредственно предшест­вующего толчка, и не зависит от того, как она двигалась под дейст­вием остальных предшествующих толчков.

Таким образом, случайное блуждание—пример однородной цепи Маркова с дискретным временем.

Далее ограничимся элементами теории конечных одно­родных цепей Маркова.

Переходной вероятностью р_ij называют условную вероятность того, что из состояния i (в котором система оказалась в результате некоторого испытания, безраз­лично какого номера) в итоге следующего испытания система перейдет в состояние j.

Таким образом, в обозначении р_ij первый индекс ука­зывает номер предшествующего, а второй—номер после­дующего состояния. Например, p₁₁—вероятность «пере­хода» из первого состояния в первое; р₂₃—вероятность перехода из второго состояния в третье.

Пусть число состояний конечно и равно k.

Матрицей перехода системы называют матрицу, ко­торая содержит все переходные вероятности этой сис­темы: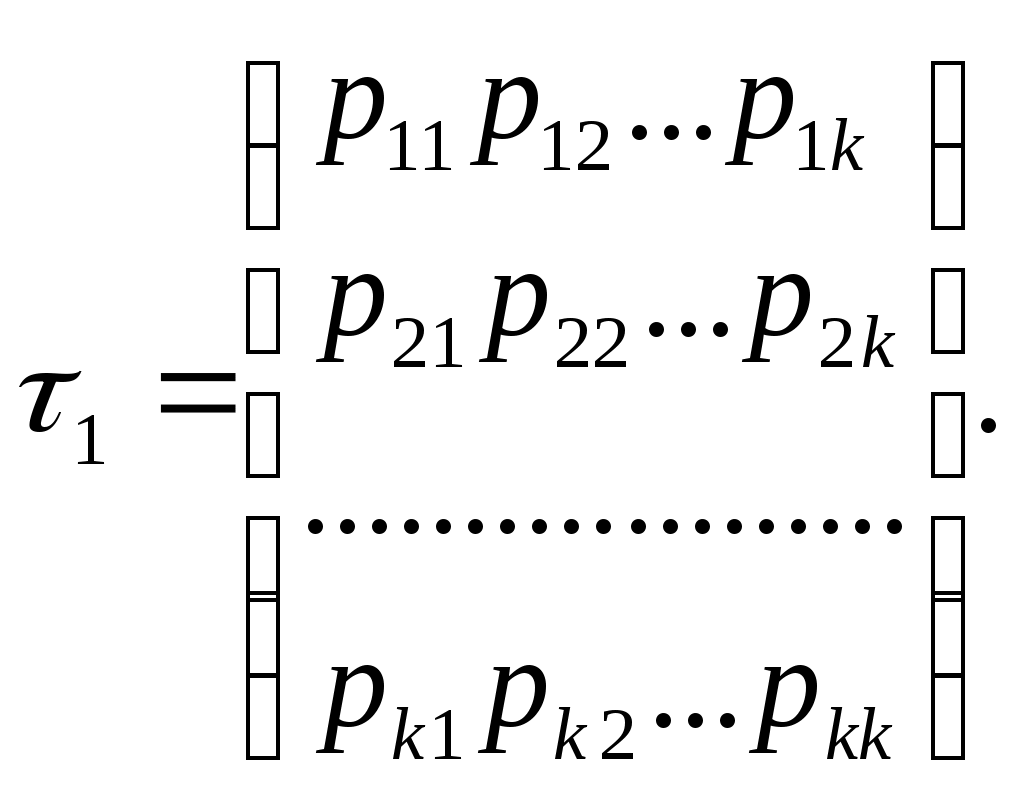



Так как в каждой строке матрицы помещены вероят­ности событий (перехода из одного и того же состояния i в любое возможное состояние j). которые образуют полную группу, то сумма вероятностей этих событий равна единице. Другими словами, сумма переходных вероятностей каждой строки матрицы перехода равна единице:



Приведем пример матрицы перехода системы, которая может находиться в трех состояниях: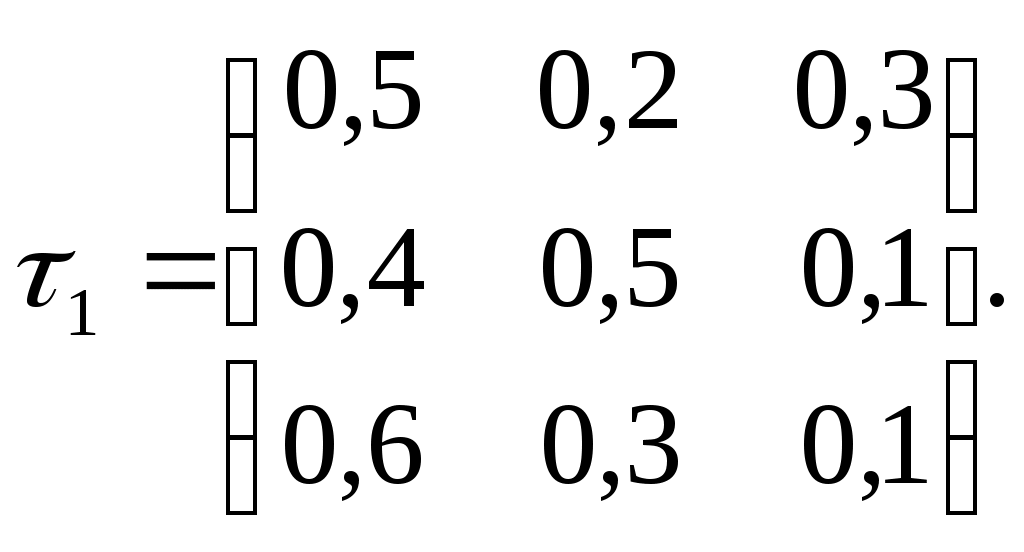



Здесь р₁₁=0,5—вероятность перехода из состояния j=1 в это же состояние j=1; р₂₁=0,4—вероятность перехода из состояния i=2 в состояние j=2. Анало­гичный смысл имеют остальные элементы матрицы.
§ 3. Равенство Маркова

Обозначим через Р_ij(п) вероятность того, что в результате п шагов (испытаний) система перейдет из состояния i в состояние j. Например, Р₂₅(10)—вероят­ность перехода за 10 шагов из второго состояния в пятое. Подчеркнем, что при п = 1 получим переходные веро­ятности

Р_ij(1)=p_ij.

Поставим перед собой задачу: зная переходные веро­ятности Р_ij, найти вероятности Р_ij(п) перехода системы из состояния i в состояние j за п шагов. С этой целью введем в рассмотрение промежуточное (между i и j) состояние r. Другими словами, будем считать, что из первоначального состояния i за т шагов система перей­дет в промежуточное состояние r с вероятностью Р_ir(т), после чего за оставшиеся п—т шагов из промежуточного состояния r она перейдет в конечное состояние j с веро­ятностью Р_rj(п—т).

По формуле полной вероятности,

(*)

Эту формулу называют равенством Маркова.

Пояснение. Введем обозначения: A—интересую­щее нас событие (за п шагов система перейдет из началь­ного состояния i в конечное состояние j), следовательно, P(A)=P_ij(n); В_r(r = 1, 2, ..., k)—гипотезы (за т шагов система перейдет из первоначального состояния ( в про­межуточное состояние r), следовательно, Р(В_r)=Р_ir(m); Р_Br(A)—условная вероятность наступления А при усло­вии, что имела место гипотеза В_r (за п—т шагов система перейдет из промежуточного состояния r в конечное состояние j), следовательно, Р_Br(A)= Р_rj(п—m). По формуле полной вероятности,

,

или в принятых нами обозначениях

,

что совпадает с формулой (*) Маркова.

Покажем, что, зная все переходные вероятности р_ij=Р_ij(1), т. е. зная матрицу τ₁ перехода из состояния в состояние за один шаг, можно найти вероятности Р_ij(2) перехода из состояния в состояние за два шага, следо­вательно, и саму матрицу перехода τ₂ по известной матрице τ₂, можно найти матрицу τ₃ перехода из состоя­ния в состояние за 3 шага, и т.д.

Действительно, положив n=2, m=1 в равенстве Маркова

,

получим



или

(**)

Таким образом, по формуле (**) можно найти все вероятности Р_ij(2), следовательно, и саму матрицу τ₂.Поскольку непосредственное использование формулы (**) оказывается утомительным, а матричное исчисление ведет к цели быстрее, напишем вытекающее из (**) соотноше­ние в матричной форме:

τ₂=τ₁ τ₁=τ₂²

Положив n=3, m =2 в (*), аналогично получим

τ₃=τ₁τ₂=τ₁τ₁²=τ₁³.

В общем случае

τ_n=τ₁ⁿ
Пример. Задана матрица перехода 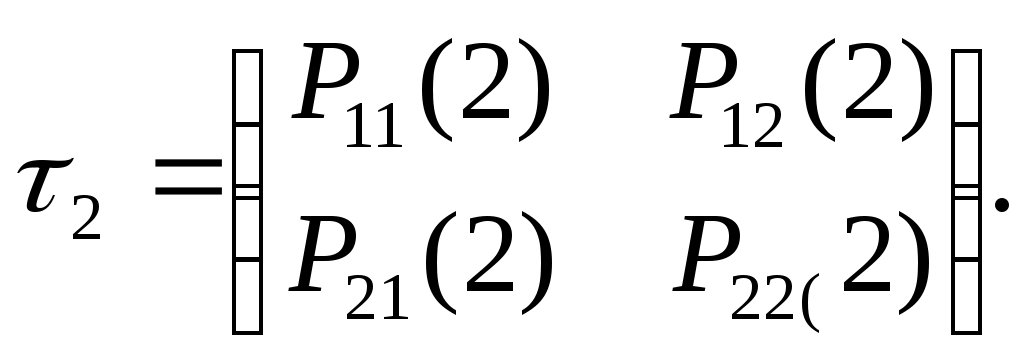Найти матрицу перехода

Решение. Воспользуемся формулой: τ₂= τ₁²:



Перемножив матрицы, окончательно получим



Задачи

1. Задана матрица перехода Найти матрицу перехода τ₂.

Отв.

2. Задана матрица перехода Найти матрицу перехода τ³.

Отв.