Исследование задач о пограничном слое. ЭТО ТВОЙ ДИПЛОМ11. Численное исследование задач о движении слабых растворов полимеров. Выпускная квалификационная работа
 Скачать 0.52 Mb. Скачать 0.52 Mb.
|
ВВЕДЕНИЕИзвестно, что при добавлении небольшого количества полимера в воду вязкость и плотность получившегося раствора практически не изменяются и остаются постоянными, но его реологические свойства будут отличаться. Зафиксированное снижение сопротивления трения за счет полимерных добавок стимулировало цикл как экспериментальных работ по изучению движения водных растворов полимеров в трубах и в пограничном слое при ламинарном и турбулентном режимах течения, так и теоретических исследований. В 1904г. Л. Прандтль в своем докладе «О движении жидкости при очень малом трении», указал путь, сделавший доступным теоретическому исследованию течения жидкости с трением в практически важных случаях. А именно, исходя из теоретических соображений и некоторых простых экспериментов, Прандтль показал, что течение в окрестности тела можно разделить на две области: на область очень тонкого слоя вблизи тела (пограничный слой), где трение играет существенную роль, и на область вне этого слоя, где трением можно пренебрегать. Эта гипотеза, с одной стороны, позволила получить физически очень наглядное объяснение важной роли вязкости в проблеме сопротивления, а с другой стороны, дала возможность преодолеть математические трудности и тем самым открыла путь теоретическому исследованию течений жидкости с трением. Свои теоретические соображения Прандтль уже тогда подтвердил некоторыми очень простыми опытами в небольшом гидроканале. Теория пограничного слоя Прандтля оказалась чрезвычайно плодотворной и сразу же после своего опубликования дала мощный толчок к дальнейшему развитию исследований. Под влиянием задач, поставленных в начале прошлого столетия расцветом авиационной техники, новая теория весьма быстро развилась и вскоре превратилась, вместе с другими важными теориями в основу современной механики жидкости и газа. В качестве областей применения теории пограничного слоя стоит упомянуть о вычислении сопротивления, возникающего при обтекании тела вследствие трения жидкости о поверхность тела, о вычислении сопротивления трения корабля, профиля крыла, лопатки турбины. Особенностью пограничного слоя является его свойство допускать при некоторых обстоятельствах возникновение возвратного течения в непосредственной близости от стенки. С этим свойством связаны отрыв пограничного слоя от тела и возникновение более или менее сильных вихрей на кормовой части обтекаемого тела. Эти явления обусловливают значительное изменение распределения давления вдоль поверхности обтекаемого тела по сравнению с распределением давления в потоке без трения, что приводит к возникновению так называемого сопротивления давления обтекаемого тела. Теория пограничного слоя указывает путь к вычислению этого сопротивления. Далее, теория пограничного слоя дает ответ на важный вопрос о том, какую форму должно иметь обтекаемое тело для того, чтобы не возникало вредного отрыва потока от тела. Однако отрыв потока от тела может возникать не только при обтекании тела, но и при течении жидкости в канале. Следовательно, теория пограничного слоя дает возможность исследовать особенности течения в межлопаточных каналах гидравлических и газовых машин (насосов, турбин). Только на основе теории пограничного слоя возможно быть объяснены явления, возникающие при достижении подъемной силой крыла максимального значения и также связанные с отрывом потока. Наконец, теплопередача между телом и обтекающей его жидкостью (или газом) также связана с особенностями течения в пограничном слое. В последнее время все большее внимание уделяется развитию численных методов для решения задач о погранслое [1]. Разработка методов расчета параметров стационарного пограничного слоя позволяет более полно изучить вопросы поведения как раствора полимеров, так и обтекаемого тела. 1.Плоское течение вязкой жидкости и функция тока.Приведенные в данной главе теоретические факты, обозначения и определения соответствуют обозначениям и фактам, представленным в литературе: Шлихтинг Г. Теория пограничного слоя. - М.: Наука, 1974, - 712 с.[2], Л.Д.Ландау, Е.М.Лифшиц Гидродинамика. Теоретическая физика: т.VI.-М.: Наука. 1986.-736 с.[3]. 1.1. Уравнения Навье Стокса.Эффективная разрешимость задачи о движении тела в идеальной несжимаемой жидкости обеспечивается условием о потенциальности движения. При этом для определения потенциала скоростей получается линейная задача. В аналогичных задачах для вязкой несжимаемой жидкости движение непотенциально, требуется интегрировать нелинейную систему уравнений Навье-Стокса и уравнения неразрывности. Уравнения Навье-Стокса представляют собой систему дифференциальных уравнений движения сплошной среды (жидкости или газа), учитывающую её вязкость. Были выведены Л.Навье в 1822г. и опубликованы в 1827г. на основе упрощенной модели молекулярных взаимодействий. В 1845 Дж. Стокс в результате изучения стационарного движения несжимаемой жидкости получил эти уравнения в совр. форме с использованием законов сохранения массы и импульса для сплошной среды.1.1.1. Плоское течениеЕсли распределение скоростей в движущейся жидкости зависит только от двух координат (х и у), причем скорость параллельна плоскости ху везде, то о таком течении говорят, как о двумерном или плоском. В случае плоского течения вязкой несжимаемой жидкости, в отсутствие внешних сил система Навье-Стокса принимает вид:  , ,Где  (u, (u, ) - вектор скорости, ) - вектор скорости, -плотность, -плотность, 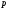 -давление, -давление, 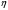 -коэффициент вязкости, -коэффициент вязкости, 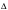 - оператор Лапласа. - оператор Лапласа.1.1.2. Функция тока.Для решения задач о двухмерном течении несжимаемой жидкости бывает удобным выражать скорость через так называемую функцию тока. Из уравнения неразрывности 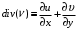 Можно заметить, что компоненты скорости могут быть записаны в виде производных от некоторой функции 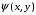 . .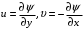 (1) (1)Данной функцией является функция тока. Уравнение непрерывности при этом удовлетворяется автоматически. Зная функцию тока, можно определить непосредственно форму линий для стационарного движения жидкости. При двухмерном течении, дифференциальное уравнение линий тока есть 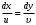 или или  . Из этого следует, что направление касательной к линии тока в каждой точке совпадает с направление скорости. Подставляя сюда (1) получим: . Из этого следует, что направление касательной к линии тока в каждой точке совпадает с направление скорости. Подставляя сюда (1) получим: , ,следовательно  . Таким образом, линии тока представляют собой семейство кривых, получающихся приравниванием функции тока . Таким образом, линии тока представляют собой семейство кривых, получающихся приравниванием функции тока 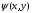 произвольной постоянной. Если между двумя точками в плоскости произвольной постоянной. Если между двумя точками в плоскости 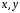 провести кривую, то поток жидкости через эту кривую будет определяться разностью значений функции тока в этих точках независимо от формы кривой. провести кривую, то поток жидкости через эту кривую будет определяться разностью значений функции тока в этих точках независимо от формы кривой. |
