Исследование задач о пограничном слое. ЭТО ТВОЙ ДИПЛОМ11. Численное исследование задач о движении слабых растворов полимеров. Выпускная квалификационная работа
 Скачать 0.52 Mb. Скачать 0.52 Mb.
|
1.2. Плоский стационарный пограничный слой.На некотором расстоянии от поверхности обтекаемого тела внутри жидкости преобладают силы инерции, действие вязкости, из-за небольшой её величины, проявляется незначительно. Скорость течения жидкости почти до самой поверхности обтекаемого тела имеет порядок скорости 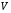 вдали от стенки. При этом картина линий тока и распределение скоростей внутри жидкости имеют вид близкий к тому, который наблюдается при потенциальном течении жидкости без трения. Но при более точных наблюдениях можно обнаружить, что жидкость, в отличие от потенциального течения, не скользит по поверхности, а прилипает к ней. Переход от нулевой скорости непосредственно на поверхности тела к полной скорости, существующей на некотором расстоянии от стенки, совершается в очень тонком слое, называемом пограничным слоем, или слоем трения. Исходя из этого, можно различать две области, между которыми нет резкой границы перехода. вдали от стенки. При этом картина линий тока и распределение скоростей внутри жидкости имеют вид близкий к тому, который наблюдается при потенциальном течении жидкости без трения. Но при более точных наблюдениях можно обнаружить, что жидкость, в отличие от потенциального течения, не скользит по поверхности, а прилипает к ней. Переход от нулевой скорости непосредственно на поверхности тела к полной скорости, существующей на некотором расстоянии от стенки, совершается в очень тонком слое, называемом пограничным слоем, или слоем трения. Исходя из этого, можно различать две области, между которыми нет резкой границы перехода.Первая область - очень тонкий слой вблизи от тела. В этой области градиент скорости 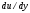 , в перпендикулярном к стенке направлении, очень велик, а вязкость , в перпендикулярном к стенке направлении, очень велик, а вязкость 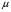 , независимо от её малой величины, оказывает значительное влияние на течение, поскольку в этом слое касательное напряжение , независимо от её малой величины, оказывает значительное влияние на течение, поскольку в этом слое касательное напряжение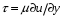 , вызванное трением, может принимать большие значения. , вызванное трением, может принимать большие значения.Вторая область- остальное течение жидкости вне пограничного слоя. Здесь градиент скорости не достигает таких больших значений, в связи с этим действие вязкости здесь не имеет на столько большого значения и можно считать, что течение здесь потенциальное. На основании некоторых точных решений уравнений Навье-Стокса было выяснено, что толщина пограничного слоя пропорциональна квадратному корню из кинематической вязкости т.е. 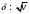 . С целью получения уравнений пограничного слоя из уравнений Навье-Стокса, принимается, что толщина этого погранслоя очень мала по сравнению с некоторым характерным размером . С целью получения уравнений пограничного слоя из уравнений Навье-Стокса, принимается, что толщина этого погранслоя очень мала по сравнению с некоторым характерным размером 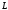 тела ( тела ( ). Исходя из этого, решения уравнений погранслоя представляют собой асимптотические решения для очень больших чисел Рейнольдса. ). Исходя из этого, решения уравнений погранслоя представляют собой асимптотические решения для очень больших чисел Рейнольдса.При упрощении уравнений Навье-Стокса для течения в пограничном слое в первую очередь необходимо произвести оценку отдельных членов этих уравнений с точки зрения порядка их величины. Принимается, что обтекаемая жидкостью стенка плоская. Ось  направляется вдоль стенки, а ось направляется вдоль стенки, а ось 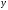 - перпендикулярно к стенке. Для обезразмеривания уравнений Навье-Стокса все скорости относятся к скорости - перпендикулярно к стенке. Для обезразмеривания уравнений Навье-Стокса все скорости относятся к скорости 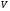 набегающего потока, а все длины- к характерному размеру тела набегающего потока, а все длины- к характерному размеру тела 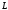 , выбираемого таким образом, чтобы безразмерная величина , выбираемого таким образом, чтобы безразмерная величина 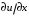 не превышала по порядку единицу в рассматриваемой области. Обезразмеривание давления и времени происходит посредством разделения их соответственно на не превышала по порядку единицу в рассматриваемой области. Обезразмеривание давления и времени происходит посредством разделения их соответственно на 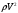 и и 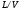 . Затем вводится число Рейнольдса . Затем вводится число Рейнольдса 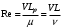 , которое должно быть очень велико. В результате уравнения Навье-Стокса для рассматриваемой задачи примут вид: , которое должно быть очень велико. В результате уравнения Навье-Стокса для рассматриваемой задачи примут вид:для направления  : :  для направления 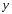 : :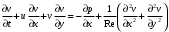 . .Безразмерным уравнением неразрывности будет 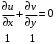 . .Граничными условиями будут: прилипание жидкости к стенкам 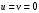 при при 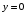 , ,и совпадение скорости 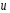 на внешнем крае погранслоя со скоростью на внешнем крае погранслоя со скоростью 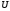 внешнего течения внешнего течения при при 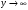 . .Для того, чтобы сделать толщину погранслоя безразмерной, нужно разделить 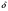 на характерный размер тела на характерный размер тела 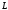 .Такая безразмерная толщина должна быть достаточно мала по сравнению с единицей, т.е. .Такая безразмерная толщина должна быть достаточно мала по сравнению с единицей, т.е. 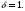 Из уравнения неразрывности видно, что величина 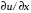 будет иметь порядок единицы, такой же, как и величина будет иметь порядок единицы, такой же, как и величина 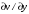 . Но в связи с тем, что на стенке скорость . Но в связи с тем, что на стенке скорость 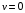 , то в пограничном слое величина скорости , то в пограничном слое величина скорости 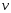 имеет порядок имеет порядок 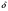 . Тогда такой же порядок . Тогда такой же порядок 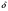 имеют в погранслое и величины имеют в погранслое и величины 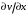 и и 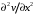 . Величина . Величина 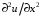 имеет порядок единицы. имеет порядок единицы.Далее принимается, что величина локального ускорения 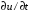 имеет такой же порядок, как и величина конвективного ускорения имеет такой же порядок, как и величина конвективного ускорения  . Это означает, что внезапные ускорения исключаются из рассмотрения. Члены, зависящие от вязкости, входят в уравнения с малым множителем . Это означает, что внезапные ускорения исключаются из рассмотрения. Члены, зависящие от вязкости, входят в уравнения с малым множителем 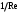 . При этом, некоторые из этих членов должны быть одного порядка с инерционными членами хотя бы в непосредственной близости от стенки. Следовательно, вблизи стенки некоторые из вторых производных скорости должны принимать очень большие значения. На основе вышесказанного, такими производными могут быть только . При этом, некоторые из этих членов должны быть одного порядка с инерционными членами хотя бы в непосредственной близости от стенки. Следовательно, вблизи стенки некоторые из вторых производных скорости должны принимать очень большие значения. На основе вышесказанного, такими производными могут быть только 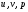 и и 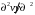 . Так как составляющая скорости, параллельная к стенки, изменяется в очень тонком слое, имеем толщину . Так как составляющая скорости, параллельная к стенки, изменяется в очень тонком слое, имеем толщину 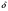 , от нуля на стенке до единицы на границе с внешним течением, то , от нуля на стенке до единицы на границе с внешним течением, то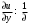 и и 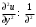 , ,в то время как 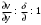 и и 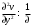 , ,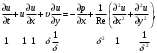 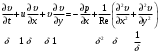 . .Можно заметить, что величина членов, зависящих от вязкости, имеет в пограничном слое одинаковый порядок с инерционными членами только в случае, когда величина числа Рейнольдса имеет порядок 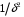 т.е. т.е. 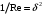 . .Таким образов, для течения, в котором число Рейнольдса достаточно велико, можно упростить первое уравнение движения, отбросив для этого величину 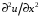 , как значительно малую по сравнению с , как значительно малую по сравнению с  . Уравнение неразрывности при этом останется неизменным для больших значений числа Рейнольдса. Из второго уравнения движения видно, что величина . Уравнение неразрывности при этом останется неизменным для больших значений числа Рейнольдса. Из второго уравнения движения видно, что величина 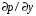 имеет порядок имеет порядок 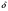 ; следовательно, величина разности давлений поперек пограничного слоя, имеет порядок ; следовательно, величина разности давлений поперек пограничного слоя, имеет порядок 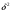 , т.е. очень мала, и поэтому давление в поперечном направлении погранслоя остается практически неизменным. Его можно принять равным давлению, существующему на внешнем крае пограничного слоя, которое определяется течением без трения. Исходя из этого, давление в пограничном слое создается внешним течением, и его следует рассматривать, как известную функцию, зависящую только от продольной координаты , т.е. очень мала, и поэтому давление в поперечном направлении погранслоя остается практически неизменным. Его можно принять равным давлению, существующему на внешнем крае пограничного слоя, которое определяется течением без трения. Исходя из этого, давление в пограничном слое создается внешним течением, и его следует рассматривать, как известную функцию, зависящую только от продольной координаты  и от времени и от времени  . .На внешней границе пограничного слоя продольная скорость  переходит в скорость внешнего течения переходит в скорость внешнего течения 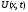 . Т.к. в этой области нет сильного градиента скорости в перпендикулярном к стенке направлении, то при большом числе Рейнольдса в уравнении отпадают все члены, зависящие от вязкости, и оно при возврате к размерным величинам примет вид . Т.к. в этой области нет сильного градиента скорости в перпендикулярном к стенке направлении, то при большом числе Рейнольдса в уравнении отпадают все члены, зависящие от вязкости, и оно при возврате к размерным величинам примет вид Для стационарного течения 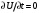 , а давление зависит только от , а давление зависит только от  , тогда уравнение после замены частных производных на обыкновенные принимает вид: , тогда уравнение после замены частных производных на обыкновенные принимает вид: Проинтегрировав это уравнение, получится уравнение Бернулли 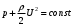 . .Граничные условия для внешнего течения приближенно такие же, как для течения без трения. Пограничный слой очень тонок, а поперечная скорость  на его внешнем крае очень мала. Следовательно, потенциальное обтекание рассматриваемого тела, имеющее на стенках нормальную составляющую скорости, равную нулю, можно рассматривать как весьма хорошее приближение для внешнего течения вязкой жидкости. Поэтому для определения перепада давления в продольном направлении погранслоя достаточно составить уравнение Бернулли для совпадающей со стенкой линии тока потенциального течения. на его внешнем крае очень мала. Следовательно, потенциальное обтекание рассматриваемого тела, имеющее на стенках нормальную составляющую скорости, равную нулю, можно рассматривать как весьма хорошее приближение для внешнего течения вязкой жидкости. Поэтому для определения перепада давления в продольном направлении погранслоя достаточно составить уравнение Бернулли для совпадающей со стенкой линии тока потенциального течения.Итого после всех выполненных упрощений от двух уравнений Навье-Стокса остается только одно, которое принимает вместе с уравнением неразрывности следующий вид: 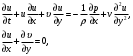 С граничными условиями 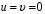 при при 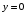 ; ; 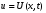 при при 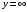 . .Полученная система уравнений называется уравнениями Прандтля для пограничного слоя. Скорость 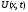 следует рассматривать, как известную функцию, определяющую распределение давления. Также для начального момента времени следует рассматривать, как известную функцию, определяющую распределение давления. Также для начального момента времени 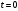 должно быть задано течение в пограничном слое во всей области рассматриваемых значений должно быть задано течение в пограничном слое во всей области рассматриваемых значений  и и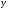 . .Для стационарного течения система уравнений принимает более простой вид: 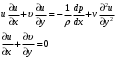 с граничными условиями 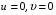 при при 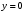 ; ; 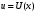 при при 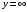 . .Также в начальном поперечном сечении 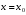 должен задаваться начальный профиль скоростей должен задаваться начальный профиль скоростей 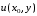 . Исходя из этого, задача расчета течения в пограничном слое сводится к расчету дальнейшего развития заданного начального профиля продольных скоростей при заданном потенциальном течении. . Исходя из этого, задача расчета течения в пограничном слое сводится к расчету дальнейшего развития заданного начального профиля продольных скоростей при заданном потенциальном течении.Полученное Прандтлем упрощение уравнений Навье-Стокса весьма значительно, поскольку из трех первоначальных уравнений плоской задачи с переменными 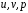 одно уравнение (уравнение движения, перпендикулярного к стенке) полностью отпадает. В результате число неизвестных сокращается на единицу, и остается лишь система уравнений с двумя неизвестными одно уравнение (уравнение движения, перпендикулярного к стенке) полностью отпадает. В результате число неизвестных сокращается на единицу, и остается лишь система уравнений с двумя неизвестными 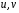 . Давление не является неизвестной величиной т.к. оно может быть получено из уравнения Бернулли для потенциального течения около рассматриваемого тела, при этом данное течение следует считать заданным. Также, в единственном из оставшихся уравнении движения теперь отсутствует один из двух членов, зависящих от вязкости. . Давление не является неизвестной величиной т.к. оно может быть получено из уравнения Бернулли для потенциального течения около рассматриваемого тела, при этом данное течение следует считать заданным. Также, в единственном из оставшихся уравнении движения теперь отсутствует один из двух членов, зависящих от вязкости.2. Задача о стационарном пограничном слое при обтекании пластины слабым водным раствором полимера в переменных Мизеса. Изложение данного пункта основывается на книге Шлихтинга [2].и статьеВ.В. Пухначев , А.Г. Петрова, О.А. Фроловская Растворы полимеров и их математические модели[4]. 2.1 Модель Павловского течения растворов полимеров. Первая математическая модель движения водного раствора полимеров, учитывающая их релаксационные свойства, была сформулирована в работе Войткунского, Амфилохиева и Павловского [5]. Авторы исходили из варианта модели максвелловского типа для вязкоупругой жидкости. Искомыми функциями в этой модели являются вектор скорости 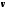 и давление жидкости и давление жидкости 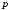 . Среда предполагается несжимаемой с постоянными плотностью . Среда предполагается несжимаемой с постоянными плотностью 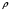 и кинематической вязкостью и кинематической вязкостью 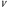 . Определяющее реологическое соотношение в этой модели имеет вид: . Определяющее реологическое соотношение в этой модели имеет вид: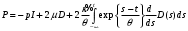 (1) (1)Здесь 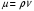 – динамическая вязкость, – динамическая вязкость, 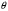 – время релаксации, – время релаксации, 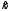 - релаксационная вязкость, - релаксационная вязкость, 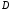 - тензор скоростей деформаций, соответствующий векторному полю - тензор скоростей деформаций, соответствующий векторному полю 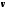 , символ , символ 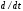 означает оператор полного дифференцирования по времени, так что означает оператор полного дифференцирования по времени, так что 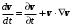 . Величины . Величины 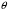 и и 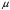 также считаются постоянными. Эта модель содержит два дополнительных параметра по сравнению с классической моделью Навье-Стокса: время релаксации и релаксационную вязкость. также считаются постоянными. Эта модель содержит два дополнительных параметра по сравнению с классической моделью Навье-Стокса: время релаксации и релаксационную вязкость.Затем в работе Павловского [6] эта модель была упрощена и использовалась для описания турбулентного пограничного слоя в предельном случае малых времен релаксации. Реологическое соотношение в этой модели после удержания первого члена в асимптотическом разложении тензора напряжений (1) по параметру 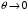 принимает вид принимает вид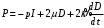 Математическая модель движения водных растворов полимеров, имеет вид [8] 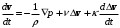 , , 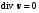 . .2.2 Уравнения пограничного слоя при обтекании тонкой пластины раствором полимеров. Эффект Томса [7] состоит в существенном увеличении критического числа Рейнольдса при внесении в воду небольшого количества растворимого полимера. Ниже выводятся уравнения ламинарного пограничного слоя в модели Павловского в случае плоских движений. В координатной записи уравнения импульса и неразрывности имеют вид 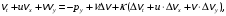 (2) (2)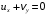 где 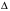 – оператор Лапласа по переменным – оператор Лапласа по переменным 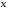 и и 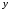 . Уравнения системы (8) следует привести к безразмерному виду. Важно учитывать неравноправие продольной координаты . Уравнения системы (8) следует привести к безразмерному виду. Важно учитывать неравноправие продольной координаты 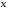 и поперечной координаты и поперечной координаты 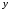 вместе с различием характерных масштабов продольной и поперечной компонент скорости: вместе с различием характерных масштабов продольной и поперечной компонент скорости: 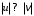 . Тогда исключается ситуация, когда . Тогда исключается ситуация, когда 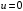 внутри области течения, за исключением твердой части границы, где выполняется условие прилипания. Ниже предполагается, что функция внутри области течения, за исключением твердой части границы, где выполняется условие прилипания. Ниже предполагается, что функция 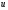 положительна. положительна. В качестве характерного масштаба скорости 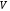 вводится скорость набегающего потока, а за характерный продольный масштаб длины берется длина обтекаемого контура вводится скорость набегающего потока, а за характерный продольный масштаб длины берется длина обтекаемого контура  . Тогда характерное время определится как . Тогда характерное время определится как 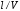 . Что касается характерного поперечного масштаба длины, то здесь имеется две возможности. В классической теории пограничного слоя она определяется как . Что касается характерного поперечного масштаба длины, то здесь имеется две возможности. В классической теории пограничного слоя она определяется как  , где , где 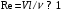 – число Рейнольдса. Но в обсуждаемой задаче есть еще один масштаб длины – число Рейнольдса. Но в обсуждаемой задаче есть еще один масштаб длины 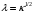 . Предполагается, что параметр . Предполагается, что параметр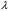 является малым. Именно этот параметр выбирается в качестве поперечного масштаба длины. Тогда переход к безразмерным переменным осуществляется по формулам является малым. Именно этот параметр выбирается в качестве поперечного масштаба длины. Тогда переход к безразмерным переменным осуществляется по формулам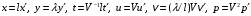 Если опустить верхний индекс у безразмерных величин, получатся уравнения: 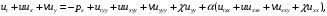 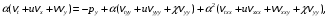 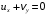 где 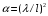 . Предельный переход в этой системе при . Предельный переход в этой системе при 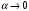 приводит к уравнениям приводит к уравнениям (3) (3)В системе (9) имеется единственный безразмерный параметр 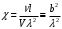 . .Этот параметр может оказаться малым за счет малости коэффициента 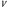 или больших значений величины или больших значений величины 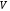 . При этом величина числа Рейнольдса не должна быть слишком большой, чтобы движение оставалось ламинарным. Важно отметить, что параметр . При этом величина числа Рейнольдса не должна быть слишком большой, чтобы движение оставалось ламинарным. Важно отметить, что параметр 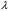 не зависит от характеристик течения и определяется только реологическими свойствами, заложенными в модель водного раствора полимера. не зависит от характеристик течения и определяется только реологическими свойствами, заложенными в модель водного раствора полимера.Может случиться, что величина  много меньше много меньше 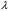 . Тогда имеет смысл перейти в системе (3) к пределу, . Тогда имеет смысл перейти в системе (3) к пределу, 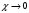 . В случае стационарного течения мы приходим к уравнениям . В случае стационарного течения мы приходим к уравнениям (4) (4)Пусть 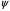 – функция тока, – функция тока, 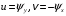 . Если ввести функцию . Если ввести функцию 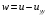 , то система (4) сводится к уравнению , то система (4) сводится к уравнению 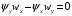 . Это означает, что . Это означает, что 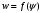 , а функция , а функция 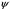 удовлетворяет уравнению удовлетворяет уравнению 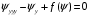 . Оно имеет простое решение, когда . Оно имеет простое решение, когда 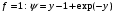 . . 2.3 Переменные Мизеса в задаче о пограничном слое при обтекании тонкой пластины раствором полимеров. 2.3.1 Переменные Мизеса в вязкой жидкости В 1927г. Р. Мизес указал на возможность примечательного преобразования уравнений пограничного слоя в вязкой жидкости к виду, более четко раскрывающему их математические особенности. Для такого преобразования прямоугольные координаты 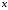 и и 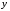 заменяются новыми независимыми переменными: координатой заменяются новыми независимыми переменными: координатой 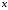 и функцией тока и функцией тока 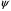 . Вычислим в новых координатах . Вычислим в новых координатах 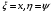 производные производные 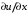 и и 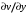 . Имея ввиду, что . Имея ввиду, что 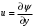 , ,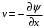 , ,можем найти 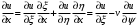 , ,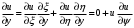 , ,Внеся эти выражения в уравнение 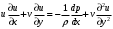 , (5) , (5)получим: 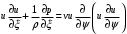 . .Далее, введем так называемое полное давление 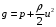 Тогда предыдущее уравнение, если вновь перейти от 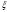 к к  , примет вид , примет вид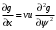 , (6) , (6)также важно учитывать, что теперь 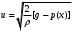 . .Таким образом получается дифференциальное уравнения для определения полного давления 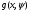 . Граничными условиями будут: . Граничными условиями будут: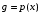 при при 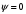 ; ; 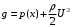 при при 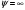 . .Для получения картины течения в плоскости 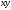 следует перейти от переменной следует перейти от переменной 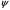 опять к переменной опять к переменной 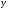 посредством преобразования посредством преобразования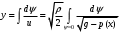 . .Преобразованное уравнение полного давления сходно с уравнением теплопроводности. В самом деле, уравнение одномерного распространения тепла, например в стержне, имеет вид  , (7) , (7)где 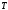 - температура, - температура,  -время, -время,  - координата, измеряющая длину, - координата, измеряющая длину,  - коэффициент температуропроводности. Правда, уравнение (6), в отличие от уравнения (7), нелинейное, так как в него вместо температуропроводности - коэффициент температуропроводности. Правда, уравнение (6), в отличие от уравнения (7), нелинейное, так как в него вместо температуропроводности  входит величина входит величина 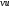 , зависящая как от независимой переменной , зависящая как от независимой переменной  , так и от зависимой переменной , так и от зависимой переменной 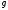 . На стенке, где . На стенке, где 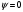 , , , ,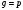 , уравнение (6) имеет неудобную для исследования особую точку. Левая часть уравнения принимает на стенке значение , уравнение (6) имеет неудобную для исследования особую точку. Левая часть уравнения принимает на стенке значение 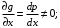 в правой же части имеем множитель  , следовательно, , следовательно, 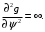 Существование этой особой точки внутренне связано с особым поведением профиля скоростей на стенке, обусловленным контурными связями, и сильно затрудняет выполнение численного интегрирования. 2.3.2 Переменные Мизеса в случае раствора полимеров В системе (4) первое уравнение этой системы является нелинейным уравнением 3-го порядка. Для понижения порядка вводится новая функция (ссылка на статью ) 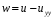 (8) (8)В качестве аргументов теперь выступают х и 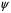 [2]. В качестве новых функций возьмем : [2]. В качестве новых функций возьмем :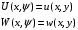 (8) преобразуется к виду 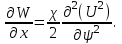 (9) (9)Первое уравнение системы (4) переходит в  (10) (10)Из условий (5) следуют краевые условия для функции U:  (11) (11)Условие (6) порождает начальное условие для функции W  (12) (12)где функция  удовлетворяет условиям согласования. удовлетворяет условиям согласования.В результате возникает формулировка начально-краевой задачи в переменных Мизеса: найти функции 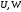 , удовлетворяющие уравнениям (9)-(10) в полуполосе , удовлетворяющие уравнениям (9)-(10) в полуполосе 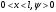 и условиям (11)-(12) на части её границы. и условиям (11)-(12) на части её границы.Краевая задача (9)-(12) для системы нелинейных, вырождающихся на левой границе уравнений до сих пор не исследована. Вопросы о существовании и единственности решения остаются открытыми. 3. Численное исследование задачи о пограничном слое в переменных Мизеса. 3.1 Нахождение функции U при заданной функции W. Решаем задачу 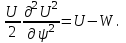 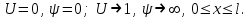 с заданной функцией 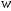 , удовлетворяющей следующим условиям: , удовлетворяющей следующим условиям: 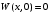 , , 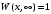 , , 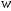 - монотонно возрастающая выпуклая вверх функция. - монотонно возрастающая выпуклая вверх функция. Уравнение представляет собой нелинейное обыкновенное дифференциальное уравнений 2-го порядка относительно функции 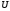 . Аргумент . Аргумент  играет роль параметра. Для этого уравнения решается краевая задача не полубесконечном интервале играет роль параметра. Для этого уравнения решается краевая задача не полубесконечном интервале 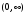 . Особенностью этого уравнения является сингулярность в 0: коэффициент при старшей производной в . Особенностью этого уравнения является сингулярность в 0: коэффициент при старшей производной в 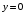 . . Стандартным методом решения краевых задач является метод стрельбы, основанный на сведении краевой задачи к задаче Коши, которая решается методом Рунге-Кутты 4-го порядка. Однако, обращение в ноль коэффициента при старшей производной сильно затрудняет численное исследование, и приводит к необходимости построения асимптотики вблизи нуля. 3.1.1 Асимптотика вблизи нуля и алгоритм численного решения. Возьмем функцию W в виде 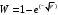 . Сделаем замену . Сделаем замену 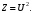 Получим краевую задачу Получим краевую задачу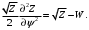 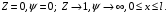 Поскольку коэффициент при второй производной искомой функции в нуле обращается в ноль, то, в силу условий согласования 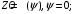 поэтому вместо краевых условий в нуле берутся краевые условия в близкой к нулю точке следующим образом: поэтому вместо краевых условий в нуле берутся краевые условия в близкой к нулю точке следующим образом: Константа α подбирается методом стрельбы так, чтобы выполнялось требуемое условие на установленных границах интервала. |
