Исследование задач о пограничном слое. ЭТО ТВОЙ ДИПЛОМ11. Численное исследование задач о движении слабых растворов полимеров. Выпускная квалификационная работа
 Скачать 0.52 Mb. Скачать 0.52 Mb.
|
3.1.2 Метод стрельбыЕсли в качестве начального значения функции  задать произвольное значение задать произвольное значение 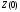 = α и решить задачу численно, то в координате = α и решить задачу численно, то в координате 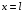 будет вычислено некоторое значение будет вычислено некоторое значение  . Очевидно, что при случайном выборе . Очевидно, что при случайном выборе 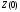 = α величина = α величина  не будет равна краевому условию, заданному для правой границы. не будет равна краевому условию, заданному для правой границы.При изменении параметра α для граничных условий решение задачи дает отличное от предыдущего значение исходной функции на правой границе,  . Исходя из этого, используется следующий алгоритм расчета. Вычисляются значения . Исходя из этого, используется следующий алгоритм расчета. Вычисляются значения 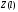 при при  и и 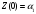 . Проводится анализ, как при изменении величины α, изменилась величина . Проводится анализ, как при изменении величины α, изменилась величина 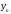 : стала ли она «ближе» к величине, указанной для правой границы, или «дальше». По результатам анализа определяется новая величина параметра α и повторяется расчет. Многократным заданием величины α можно добиться совпадения вычисленной величины : стала ли она «ближе» к величине, указанной для правой границы, или «дальше». По результатам анализа определяется новая величина параметра α и повторяется расчет. Многократным заданием величины α можно добиться совпадения вычисленной величины  с величиной, указанной для правой границы, с заданной точностью расчета. с величиной, указанной для правой границы, с заданной точностью расчета.Таким образом, метод стрельбы не решает краевую задачу в исходной постановке, а сводит ее к последовательности более простых задач с особым образом сформулированными начальными условиями. 3.1.3 Метод Рунге-Кутты 4-го порядка Рассматривается задача Коши для системы обыкновенных дифференциальных уравнений первого порядка. 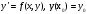 Тогда приближенное значение в последующих точках вычисляется по итерационной формуле:  Вычисление нового значения проходит в четыре стадии: 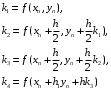 3.1.4 Вычисление функции U Суть описываемого численного исследования заключается в подборе второго начального условия методом стрельбы. Для того, чтобы найти это условие, берется начальный отрезок и делится на части. После этого происходит «прогонка» начальных условий с некоторым шагом. В результате находится шаг, при котором было обнаружено самое точное значение. Затем окрестности этой точки на 1 шаг в каждую сторону заменяют начальный отрезок, который снова делится на шаги. Алгоритм повторяется вплоть до достижения значения правой границы с выбранной точностью расчета. В связи с невозможностью буквального выполнения левого краевого условия 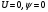 при численном решении, в процессе исследования была обнаружена высокая чувствительность функции к начальному значению производной (являющейся непосредственно вторым условием) и фиксированного шага для метода Рунге-Кутты 4-го порядка. при численном решении, в процессе исследования была обнаружена высокая чувствительность функции к начальному значению производной (являющейся непосредственно вторым условием) и фиксированного шага для метода Рунге-Кутты 4-го порядка. Ниже представлены графические результаты решения задачи при различном числе итераций метода стрельбы и полученные соответствующие значения второго начального условия (код для построения графиков написан на языке MatLab и представлен в приложении): 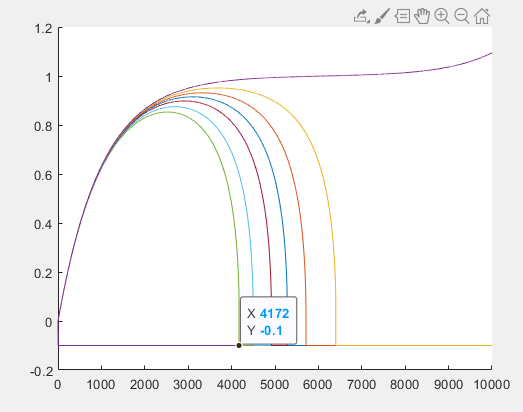 Рисунок 1. График по числу шагов с значением проходов метода стрельбы 1. 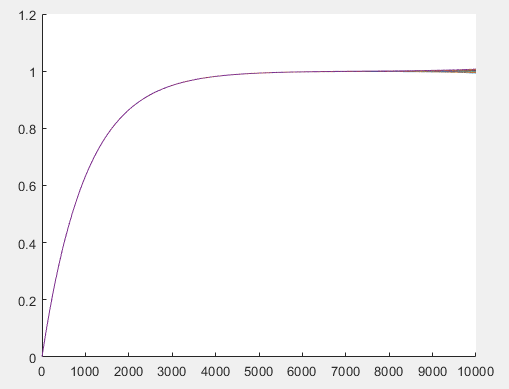 Рисунок 2. График по числу шагов с значением проходов метода стрельбы 5.  Рисунок 3. График по числу шагов с значением проходов метода стрельбы 5. 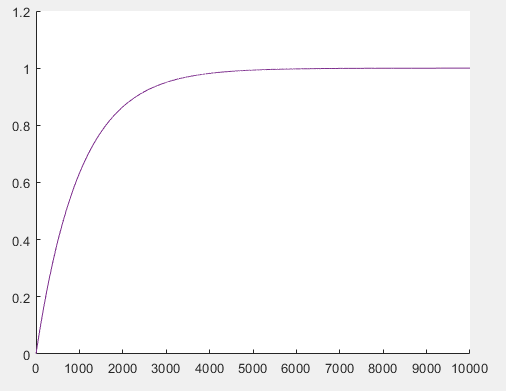 Рисунок 4. График по числу шагов с значением проходов метода стрельбы 10.  Рисунок 5. График по числу шагов с значением проходов метода стрельбы 10. Очевидно, что с ростом числа итераций метода стрельбы, итоговая точность решения значительно повышается. Визуально это выражено в постепенном схождении графиков к асимптоте. Таблица 1 наглядно демонстрирует повышение точности с ростом числа итераций метода стрельбы.
Таблица 1. Сравнение полученных значений второго начального условия в зависимости от кол-ва проходов метода стрельбы. 3.2 Нахождение функции W. Функция W находится из решения следующей задачи Коши для линейного обыкновенного ДУ первого порядка, относительно переменной  . . . .Данное уравнение было получены комбинацией уравнений (9) и (10) . Переменная  в данном случае играет роль параметра. в данном случае играет роль параметра. Решение этой задачи дается формулой  Используя найденное в предыдущем пункте значение U , не зависящее от x, запишем решение в виде  и найдем по этой формуле значение  . .Далее представлено сравнение графиков расчетного значения функции W и функции 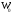 , расчеты с которой предоставлены в предыдущем пункте главы. , расчеты с которой предоставлены в предыдущем пункте главы.Рисунок 6. Сравнение графиков 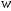 и и 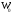 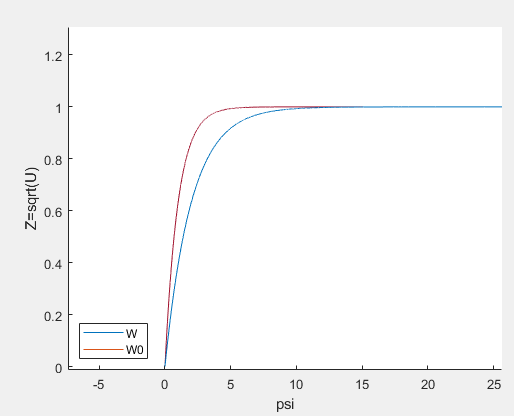 Заключение В процессе выполнения работы было изучено применение переменных Мизеса для задач ламинарного пограничного слоя течения вязкой жидкости. Для задачи обтекания плоской пластины слабым водным раствором полимеров (модель Павловского) также были введены переменные Мизеса и рассмотрена краевая задача на полубесконечном интервале для системы двух нелинейных уравнений. ( аналог задачи Блазиуса для раствора полимера). Произведено численное исследование задачи. Построен и реализован алгоритм нахождения скорости в переменных Мизеса с использованием асимптотики в нуле. Далее предполагается решение двух связанных нелинейных задач методом итераций и на этом пути сделан первый шаг, показавший вполне правдоподобный результат. Библиографический список 1. Покровский А.Н. Об одном представлении решения уравнения Блазиуса и его приложениях // Механика жидкости и газа. 1975. № 3. С. 143 - 146. 2. Шлихтинг Г. Теория пограничного слоя. - М.: Наука, 1974, - 712 с. 3. Л.Д.Ландау, Е.М.Лифшиц Гидродинамика. Теоретическая физика: т.VI.-М.: Наука. 1986.-736 с. 4. В.В. Пухначев1,2, А.Г. Петрова1,3, О.А. Фроловская Растворы полимеров и их математические модели.// Известия высших учебных заведений. Северо-Кавказский регион. Естественные науки. 2020. С.82-91. 5. Войткунский Я.И., Амфилохиев В.Б., Павловский В.А. Уравнения движения жидкости с учетом ее релаксационных свойств // Труды Ленинградского ордена Ленина кораблестроительного института. 1970. Т. 69. С. 19–26. 6.Павловский В.А. К вопросу о теоретическом описании слабых водных растворов полимеров // ДАН СССР. 1971. Т. 200. № 4. С. 809–812. 7.Toms B.A. Some observations on the flow of linear polymer solutions through straight tubes at large Reynolds number // In: Proceedings of the First International Congress on Rheology. Holland. 1948. Vol. 2. P. 135–141. Amsterdam. The Netherlands 8.Овсянников М.К., Орлова Е.Г., Емельянов П.С. Основы гидромеханики.-М.: РКонусльт, 2003г. – 160с. 9..Meleshko S.V., Pukhnachev V.V. Group Analysis of the Boundary Layer Equations in the Model of Polymer Solutions // Symmetry, 2020, 12, 1084-1103. 10.Самарский А.А., Гулин А.В, Численные методы: Учеб. Пособие для вузов.-М.: Наука. 1989.-432с. 11. Л.И.Седов Механика сплошной среды. Том 2. М.: Наука, 1970 г., 568 стр. Приложение. Программа для метода стрельбы clear; clc; format long g; a = 0.001; b = 10; yinfty = 1; h = 0.001; hold on; h_start = 0.01; h_end = 1; h_step = (h_end - h_start)/10; h_stepK=h_step; whIndex = 0; a1 = [a*(h_start-h_step) (h_start-h_step)]; [x, y_temp] = RungeKutta(a,b,h,a1,@fun); L = length(y_temp(1,:)); while whIndex < 1 clear yTest NaNArray testArray h_current; clear AllSeparationPoints SeparationPoinsStart SeparationPointsEnd ; countS = 0; for i = h_start:h_step:h_end countS = countS + 1; h_current(countS) = i; if i == 0 i = 0.000001; end alpha=i; y0 = alpha*a; a1 = [y0 alpha]; [x, y] = RungeKutta(a,b,h,a1,@fun); y_temp = y; disp(i); yTest(countS,:) = y(1,:); end hold off; testArray = zeros(1,countS); for i = 1:1:countS for j = 1:1:L if yTest(i,j) > 2 yTest(i,j) = 2; end if yTest(i,j) < 0 yTest(i,j) = -0.1; end end end for i = 1:1:countS for j = 1:1:L-1 if (yTest(i,j) == -0.1) && isnan(yTest(i,j+1)) yTest(i,j+1) = -0.1; end end end for i = 1:1:countS if isnan(yTest(i,L)) for j = 1:1:L-1 yTest_R(i,j) = yTest(i,j+1) - yTest(i,j); end end end for i = 1:1:countS if isnan(yTest(i,L)) maxR(i) = yTest_R(i,1); for j = 2:1:L-1 if maxR(i) < yTest_R(i,j) maxR(i) = yTest_R(i,j); yTest_jump(i) = j; end end end end for i = 1:1:countS if (isnan(yTest(i,L))) && maxR(i)>0.5 for j = yTest_jump(i) - 5:1:L yTest(i,j) = -0.1; end end end for i = 1:1:countS-1 if (yTest(i,L) - 1) *(yTest(i+1,L) - 1) < 0 SeparationPoint = i+1; end end h_start = h_current(SeparationPoint - 1); h_end = h_current(SeparationPoint); h_step = (h_end - h_start)/10; disp(whIndex); whIndex = whIndex+1; end hold on for i = 1:1:countS % plot(yTest(i,:)); plot(x,y(1,:)); % plot(x,y(1,:),x,y(2,:),x,W(1,:)); % plot(x,y(1,:),x,W(1,:)); xlabel('psi') ylabel('Z=sqrt(U)') legend({'W','W0'},'location','southwest') % plot(x,W); end hold off function out = fun(x,y) out(1) = y(2); out(2) = ((1-exp(-x))*(2*exp(-2*x)-exp(-x)-1))/(y(1))^2 + (1 - (y(2))^2) /(y(1)); end function [x y] = RungeKutta(a,b,h,con,fun) x = a:h:b; n = length(x); y = zeros(length(con),n); y(:,1) = con; for k = 1:(n-1) k1 = fun(x(k),y(:,k)); k2 = fun(x(k)+0.5*h,y(:,k)+0.5*h*k1'); k3 = fun(x(k)+0.5*h,y(:,k)+0.5*h*k2'); k4 = fun(x(k)+h,y(:,k)+h*k3'); y(:,k+1)=y(:,k)+h*(k1'+2*k2'+2*k3'+k4')/6; end Выпускная квалификационная работа выполнена мной совершенно самостоятельно. Все использованные в работе материалы и концепции из опубликованной научной литературы и других источников имеют ссылки на них. «__» ___________ 2021 г. ______________________ (_______________) (подпись) (Ф.И.О) |

