Цифровые устройства. Что такое цифровые микросхемы. Виды цифровых микросхем

• Название: Что такое цифровые микросхемы. Виды цифровых микросхем
• Анкор: Цифровые устройства.doc
• Дата: 22.09.2017
• Размер: 2.25 Mb.
• Имя файла: Цифровые устройства.doc
• Тип: Документы; #8922
• страница: 9 из 38

Регенерация цифрового сигнала (Триггер Шмитта)

Микросхемы соединяются между собой печатными проводниками или плоскими кабелями. При распространении цифрового сигнала по этим проводникам он неизбежно искажается. В основном это выражается в затягивании фронтов и поэтому на приёмном конце его приходится восстанавливать. Кроме того, часто приходится подавать на вход цифрового устройства обычные аналоговые сигналы (например, с выхода приёмника). Примерная форма сигнала на входе цифровой микросхемы приведена на рисунке 6.1.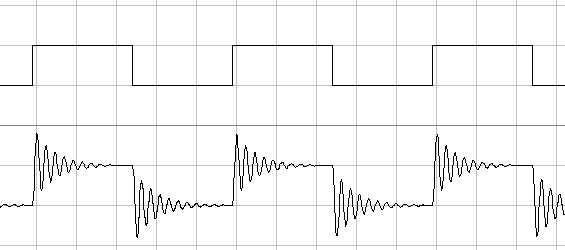

 
Рисунок 6.1. Пример сигнала на входе цифровой микросхемы

Как видно из приведённого рисунка, сигнал на входе микросхемы может принимать любые значения, в том числе и запрещённые для цифровых микросхем. Как уже обсуждалось ранее, это может привести к выходу цифровых микросхем из строя.

Для того, чтобы можно было обрабатывать такие сигналы, применяются специальные схемы, такие как триггеры Шмитта. Триггер Шмитта представляет собой устройство охваченное положительной обратной связью. Наличие положительной обратной связи приводит к практически мгновенному изменению напряжения на выходе схемы при превышении входным сигналом порогового напряжения. Схема триггера Шмитта, построенная на двух инверторах приведена на рисунке 6.2.

 
Рисунок 6.2. Схема триггера Шмитта

В этой схеме положительная обратная связь образуется двумя резисторами. Глубина обратной связи определяется соотношением между этими резисторами. То, что часть сигнала с выхода схемы триггера Шмитта подаётся на её вход, приводит к тому, что вместо одного порога у неё имеется два порога. Один порог называется порогом срабатывания схемы (когда на выходе триггера Шмитта формируется единичный уровень). Второй порог называется порогом отпускания (когда на выходе триггера Шмитта формируется нулевой уровень). Из-за наличия двух порогов триггер Шмитта имеет ещё одно название — схема с гистерезисом.

Наличие двух порогов отчётливо видно на рисунке 6.3, где на вход триггера Шмитта подано синусоидальное напряжение. Входной и выходной сигналы исследуемой схемы на этом рисунке совмещены. В результате пороги срабатывания триггера Шмитта можно определить по точкам пересечения синусоиды и выходного сигнала.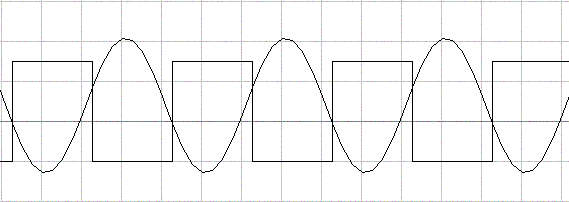

 
Рисунок 6.3. Преобразование синусоидального сигнала в логический при помощи триггера Шмитта

Благодаря двум порогам схема нечувствительна к шумам на её входе. Ведь если триггер Шмитта перешёл в другое состояние, то для того, чтобы вернуть его в прежнее состояние нужно приложить напряжение, превышающее разность его порогов. Такое полезное свойство триггера Шмитта привело к его широкому использованию в схемах, подверженных влиянию шумов, таких как, например, шумоподавители ЧМ приёмников.

В качестве примера можно привести сигнал на выходе компаратора при воздействии точно такого же синусоидального сигнала, как и на рисунке 6.3. Эти сигналы приведены на рисунке 6.4. Как видно из этого рисунка, в момент пересечения синусоидальным сигналом порогового уровня компаратора, на его выходе появляются усиленные шумы входного сигнала. Это приводит к формированию лишних импульсов на выходе схемы, что не всегда приемлемо для правильной работы цифрового устройства в целом.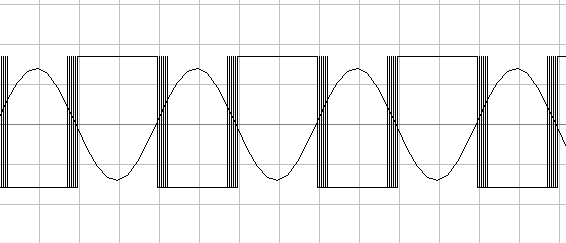

 
Рисунок 6.4. Преобразование синусоидального сигнала в логический при помощи компаратора.

Следует отметить, что наличие двух порогов не приводит к изменению логики работы цифровых устройств. Посмотрите внимательно на сигналы, приведённые на рисунке 6.3. Если сдвинуть выходной сигнал относительно входного, то точки их пересечения совместятся на одном уровне. То есть выходной сигнал триггера Шмитта можно рассматривать просто как задержанный относительно входа усиленный и ограниченный сигнал.

Ещё одно применение триггеры Шмитта нашли в качестве входных каскадов в системных шинах микропроцессоров. Мы помним, что входы цифровых микросхем нельзя бросать в воздухе, однако при работе на шину обязательным условием является возможность отключения источников цифровых сигналов от шины. Для того чтобы при этом входы цифровых микросхем не оставались в воздухе, все проводники в шине подключают к источнику питания или к корпусу при помощи внешних резисторов.

Использование в качестве входных каскадов, подключённых к системной шине, триггеров Шмитта, позволяет избавиться от этих внешних резисторов.

Перечисленные выше причины привели к широкому распространению триггеров Шмитта. Условно-графическое изображение триггера Шмитта приведено на рисунке 6.5. Символ, изображённый на рабочем поле этого логического элемента говорит о наличии гистерезиса (разности порогов срабатывания).

 
Рисунок 6.5. Условно-графическое обозначение триггера Шмитта

В настоящее время производится много готовых микросхем, в которых содержится сразу несколько триггеров Шмитта. Пороги в этих схемах установлены заранее. Например, в микросхеме 555ТЛ2 содержится сразу шесть триггеров Шмитта с разносом порогов 800 мВ.

В КМОП микросхемах пороги срабатывания и отпускания устанавливаются на трети напряжения питания. Примером подобной микросхемы может служить КМОП микросхема К1561ТЛ1, в которой содержится четыре логических элемента "2И", каждый вход которого обладает гистерезисом.

В настоящее время за рубежом широко распространены микросхемы малой логики, где в одном очень маленьком корпусе, обычно с пятью выводами, размещается одиночный логический элемент. В качестве примера одиночного триггера Шмитта можно назвать микросхемы SN74AHC1G14 или SN74LVC1G17.

Раздел 3

Арифметические основы цифровой техники.

Глава 1

Арифметические основы цифровой техники

В цифровых устройствах приходится иметь дело с различными видами информации. Это в чистом виде двоичная информация, такая как включен прибор или выключен, исправно устройство или нет. Информация может быть представлена в виде текстов, и тогда приходится буквы алфавита кодировать при помощи двоичных уровней сигнала. Достаточно часто информация может представлять собой числа. Числа могут быть представлены в различных системах счисления. Форма записи в них чисел существенно различается между собой, поэтому, прежде чем перейти к особенностям представления чисел в цифровой технике, рассмотрим их запись в различных системах счисления.

Системы счисления

Начнем с определения системы счисления. Система счисления - это совокупность правил записи чисел цифровыми знаками. Системы счисления бывают позиционные и непозиционные. В настоящее время и в технике и в быту широко используются как позиционные, так и непозиционные системы счисления. Рассмотрим сначала примеры непозиционных систем счисления.

В качестве классического примера непозиционной системы счисления обычно приводят римскую форму записи чисел. Там не менее это не единственная непозиционная система счисления, используемая в настоящее время.

Сейчас, как и в глубокой древности, для записи числа используются так называемые “палочки”. Эта форма записи чисел наиболее понятна и требует для записи числа всего один символ. Число образуется суммой этих “палочек”. Однако при записи больших чисел возникают неудобства. Число получается громоздким и его трудно читать.

В следующем варианте непозиционной системы счисления стали использовать несколько символов (цифр). Каждая цифра обозначает различное количеств единиц. Конечное число точно так же как и в предыдущем варианте образуется суммой цифр. Наиболее яркий вариант использования такой системы счисления - это денежные отношения. Мы с ними сталкиваемся каждый день. Здесь никому не приходит в голову, что сумма, которую мы выкладываем за продукты, может зависеть от того, в каком порядке мы расположим монеты на столе! Номинал монеты или банкноты не зависит от того, в каком порядке она была вынута из кошелька. Это классический пример непозиционной системы счисления.

Однако чем большее число требуется представить в такой системе счисления, тем большее количество цифр требуется для этого. Позиционные системы счисления были придуманы относительно недавно для того, чтобы сэкономить количество цифр, используемое для записи чисел.

Значение цифры в позиционной системе счисления зависит от её позиции в записываемом числе. В позиционной системе счисления появляются два очень важных понятия - основание системы счисления и вес цифры. Дело в том, что в позиционной системе счисления число представляется в виде формулы разложения:

A_p=a_npⁿ+a_n-1p^n-1+...+a₂p² +a₁p¹+a₀p⁰+a_-1p^-1+a_-2p ^-2+...+a_-kp^-k

где p - основание системы счисления
p_i - вес единицы данного разряда
a_i - цифры, разрешённые в данной системе счисления.

При этом количество цифр в системе счисления зависит от основания. Количество цифр равно основанию системы счисления. В двоичной системе счисления две цифры, в десятичной – десять, а в шестнадцатеричной – шестнадцать. Число в любой позиционной системе счисления записываются в виде последовательности цифр:

A=a_na_n-1...a₂a₁a₀,a_-1a_-2 ...a_-k,

где ai – цифры данной системы счисления, а цифра, соответствующая единицам определяется по положению десятичной запятой (или десятичной точки в англоязычных странах). Каждая цифра, использованная в записи числа, называется разрядом.

Какие же системы счисления применяются в настоящее время? Первый ответ, который я ожидаю – это десятичная система счисления. А ещё? Да, да не удивляйтесь! Мы широко используем и другие системы счисления! Достаточно посмотреть себе на левую руку. Там мы увидим часы. Сколько минут помещается в часе? Шестьдесят! Сколько секунд помещается в минуте? Шестьдесят! Налицо признаки шестидесятеричной системы счисления. Это наследование древней вавилонской системы счисления, которую вместе с компасом и часами европейцы заимствовали от арабов.

А еще примеры? Да сколько угодно! Картушка компаса делится на восемь румбов. Чем не восьмеричная система счисления? А давно ли в России отказались от полушек (четверть копейки) или грошей (половина копейки)? А следующее значение монеты – две копейки! Чем не двоичная система счисления?

Рассмотрим подробнее системы счисления, наиболее часто используемые в цифровой технике.

Десятичная система счисления

Основание этой системы счисления p равно десяти. В этой системе счисления используется десять цифр. В настоящее время для обозначения этих цифр используются символы 0, 1, 2, 3, 4, 5, 6, 7, 8, 9. Число в десятичной системе счисления записывается как сумма единиц, десятков, сотен, тысяч и так далее. То есть веса соседних разрядов различаются в  десять раз. Точно также записываются и числа, меньшие единицы. В этом случае разряды числа будут называться как десятые, сотые или тысячные доли единицы.

Рассмотрим пример записи десятичного числа. Для того чтобы показать, что в примере используется именно десятичная система счисления, используем индекс 10. Если же кроме десятичной формы записи чисел не предполагается использования никакой другой, то индекс обычно не используется:

A₁₀=247,56₁₀=2*10²+4*10¹+7*10⁰+5*10^-1 +6*10^-2=200₁₀+40₁₀+7₁₀+0,5₁₀+0,06₁₀

Здесь самый старший разряд числа будет называться сотнями. В приведённом примере сотням соответствует цифра 2. Следующий разряд будет называться десятками. В приведённом примере десяткам соответствует цифра 4. Следующий разряд будет называться единицами. В приведённом примере единицам соответствует цифра 7. Десятым долям соответствует цифра 5, а сотым – 6.

Двоичная система счисления

Основание этой системы счисления p равно двум. В этой системе счисления используется две цифры. Чтобы не выдумывать новых символов для обозначения цифр, в двоичной системе счисления были использованы символы десятичных цифр 0 и 1. Для того чтобы не спутать систему счисления в записи числа используется индекс 2. Если же кроме двоичной формы записи чисел не предполагается использования никакой другой, то этот индекс можно опустить.

Число в этой системе счисления записывается как сумма единиц, двоек, четвёрок, восьмёрок и так далее. То есть веса соседних разрядов различаются в два раза. Точно также записываются и числа, меньшие единицы. В этом случае разряды числа будут называться как половины, четверти или восьмые доли единицы.

Рассмотрим пример записи двоичного числа:

A₂=101110,101₂=1*2⁵+0*2⁴+1*2³+1*2² +1*2¹+0*2⁰+1*2^-1+0*2^-2+1*2^-3=32₁₀+8₁₀+4₁₀+2₁₀+0,5₁₀+0,125₁₀=46,625₁₀

При записи во второй строке примера десятичных эквивалентов двоичных разрядов мы не стали записывать степени двойки, которые умножаются на ноль, так как это привело бы только к загромождению формулы и, как следствие, затруднение понимания материала.

Недостатком двоичной системы счисления можно считать большое количество разрядов, требующихся для записи чисел. В качестве преимущества этой системы счисления можно назвать простоту выполнения арифметических действий, которые будут рассмотрены позднее.

Восьмеричная система счисления

Основание этой системы счисления p равно восьми. Восьмеричную систему счисления можно рассматривать как более короткий вариант записи двоичных чисел, так как число восемь является степенью числа два. В этой системе счисления используется восемь цифр. Чтобы не выдумывать новых символов для обозначения цифр, в восьмеричной системе счисления были использованы символы десятичных цифр 0, 1, 2, 3, 4, 5, 6 и 7. Для того чтобы не спутать систему счисления в записи числа используется индекс 8. Если же кроме восьмеричной формы записи чисел не предполагается использования никакой другой, то этот индекс можно опустить.

Число в этой системе счисления записывается как сумма единиц, восьмёрок, шестьдесят четвёрок и так далее. То есть веса соседних разрядов различаются в восемь раз. Точно также записываются и числа, меньшие единицы. В этом случае разряды числа будут называться как восьмые, шестьдесят четвёртые и так далее доли единицы.

Рассмотрим пример записи восьмеричного числа:

A₈=125,46₈=1*8²+2*8¹+5*8⁰+4*8^-1+6*8 ^-2=64₁₀+16₁₀+5₁₀+4₁₀/8₁₀+6₁₀/64₁₀= 85,59375₁₀

Во второй строке приведённого примера фактически осуществлён перевод числа, записанного в восьмеричной форме в десятичное представление того же самого числа. То есть мы фактически рассмотрели один из способов преобразования чисел из одной формы представления в другую.

Так как в формуле используются простые дроби, то возможен вариант, что точный перевод из одной формы представления в другую становится невозможным. В этом случае ограничиваются заданным количеством дробных разрядов.

Шестнадцатеричная система счисления

Основание этой системы счисления p равно шестнадцати. Эту систему счисления можно считать ещё одним вариантом записи двоичного числа. В этой системе счисления используется шестнадцать цифр. Здесь уже не хватает десяти цифр, поэтому приходится придумать недостающие шесть цифр.

Для обозначения этих цифр можно воспользоваться первыми буквами латинского алфавита. При записи шестнадцатеричного числа неважно буквы верхнего или нижнего регистра будут использоваться в качестве цифр. В качестве цифр в шестнадцатеричной системе используются символы 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F.

Так как здесь появляются новые цифры, то приведём таблицу соответствия этих цифр десятичным значениям.

Таблица 1.6. Таблица соответствия шестнадцатеричных цифр десятичным значениям

Шестнадцатеричная цифра	Десятичный эквивалент
0	0
1	1
2	2
3	3
4	4
5	5
6	6
7	7
8	8
9	9
A	10
B	11
C	12
D	13
E	14
F	15

Число в этой системе счисления записывается как сумма единиц, чисел шестнадцать, двести пятьдесят шесть и так далее. То есть веса соседних разрядов различаются в шестнадцать раз. Точно также записываются и числа, меньшие единицы. В этом случае разряды числа будут называться как шестнадцатые, двести пятьдесят шестые и так далее доли единицы.

Рассмотрим пример записи шестнадцатеричного числа:

A₁₆=2AF,C4₁₆=2*16²+10*16¹+15*16⁰+12*16^-1+4*16 ^-2=512₁₀+160₁₀+15₁₀+12₁₀/16₁₀+4₁₀/254₁₀= 687,765625₁₀

Из приведённых примеров записи чисел в различных системах счисления вполне очевидно, что для записи одного и того же числа с одинаковой точностью в разных системах счисления требуется различное количество разрядов. Чем больше основание системы счисления, тем меньшее количество разрядов требуется для записи одного и того же числа.

Глава 2

Преобразование чисел из одной системы счисления в другую

Достаточно часто требуется уметь переводить число из одной системы счисления в другую. Давайте научимся выполнять такое действие. Преобразование целых чисел и правильных дробей выполняется по разным правилам. В действительном числе преобразование целой и дробной части производят по отдельности.

Преобразование целых чисел

Для перевода необходимо исходное число разделить на основание новой системы счисления до получения целого остатка, который является младшим разрядом числа в новой системе счисления (единицы). Полученное частное снова делим на основание системы и так до тех пор, пока частное не станет меньше основания новой системы счисления. Все операции выполняются в исходной системе счисления.

Рассмотрим для примера перевод числа из десятичной системы счисления в двоичную систему счисления.

Возьмём десятичное число А₁₀ = 124 и поделим его на основание двоичной системы, то есть число 2. Деление будем производить уголком: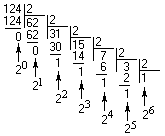



В результате первого деления получим разряд единиц (самый младший разряд). В результате второго деления получим разряд двоек. Деление продолжаем, пока результат деления больше двух. В конце операции преобразования мы получили двоичное число 1111100₂.

Теперь то же самое число переведём в восьмеричную систему счисления. Для этого число 124₁₀ разделим на число 8:

Как мы видим, остаток от первого деления равен 4. То есть младший разряд восьмеричного числа содержит цифру 4. Остаток от второго деления равен 7. то есть второй разряд восьмеричного числа – это цифра 7. Старший разряд получился равным 1. То есть в результате многократного деления мы получили восьмеричное число 174₈.

Проверим, не ошиблись ли мы в процессе преобразования? Для этого преобразуем получившееся двоичное число в десятичную систему по обычной формуле разложения:

 1×8²+7×8¹+4×8⁰=64₁₀+56₁₀+4₁₀=124

;А можно ли осуществить перевод из восьмеричной системы счисления в двоичную делением? Можно! Но деление нужно произвести по правилам восьмеричной арифметики. Правила работы в восьмеричной системе счисления мы рассмотрим в следующей главе. Тем не менее, для полноты материала, рассмотрим пример перевода в двоичную форму полученного ранее восьмеричного числа 174₈. Разделим его на основание новой системы счисления 2.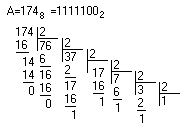



Как мы убедились выполнять деление в восьмеричной системе очень неудобно, ведь подсознательно мы делим в десятичной системе счисления. Давайте обратим внимание на то, что число 8 является степенью числа 2. То есть можно считать восьмеричную систему счисления просто более короткой записью двоичного числа. Это означает, что для представления восьмеричной цифры можно использовать три двоичных бита (8=2³). Давайте составим таблицу соответствия. Она приведена в таблице 2.1.

Таблица 2.1. Таблица соответствия восьмеричных цифр и двоичного кода

Двоичный код	Восьмеричная цифра	Десятичный эквивалент
000	0	0
001	1	1
010	2	2
011	3	3
100	4	4
101	5	5
110	6	6
111	7	7

Используя эту таблицу можно просто заменить каждую восьмеричную цифру тремя двоичными битами. Три двоичных бита обычно называют триадой или трибитом. Теперь давайте переведём восьмеричное число 1748 в двоичную форму при помощи таблицы 7:

 

Аналогично можно выполнить перевод числа из двоичной системы в восьмеричную. Для этого двоичное число разбивают на триады относительно крайнего правого разряда (или двоичной запятой) и, используя таблицу 7, каждой триаде ставят в соответствие восьмеричную цифру.

Аналогичным образом можно выполнить перевод числа из шестнадцатеричной формы в двоичную и обратно. В этом случае для представления шестнадцатеричной цифры потребуется четыре двоичных разряда. Четыре двоичных разряда обычно называют тетрадой. Иногда при переводе иностранных книг используется термин нибл.

Давайте составим таблицу соответствия двоичных тетрад и шестнадцатеричных цифр. Для этого мы будем просто прибавлять единицу к значению предыдущей строки в каждом столбце таблицы, в соответствии с используемой в этом столбце системой счисления. Результат приведён в таблице 2.2.

В качестве примера использования таблицы 2.2 переведем шестнадцатеричное число 7С₁₆ в двоичную форму представления:



Таблица 2.2 Таблица соответствия шестнадцатеричных цифр и двоичного кода

Двоичный код	Восьмеричная цифра	Десятичный эквивалент
0000	0	0
0001	1	1
0010	2	2
0011	3	3
0100	4	4
0101	5	5
0110	6	6
0111	7	7
1000	8	8
1001	9	9
1010	a	A
1011	b	B
1100	c	C
1101	d	D
1110	e	E
1111	f	F

Пример преобразования двоичного числа в восьмеричную и шестнадцатеричную форму приведён на рисунке 2.1.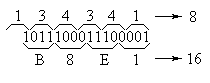



Рисунок 2.1. Пример преобразования двоичного числа в восьмеричную и шестнадцатеричную форму.

На этом рисунке внизу выделены двоичные тетрады и соответствующие им шестнадцатеричные цифры. Их соответствие можно проверить при помощи таблицы 2.2. Сверху выделены триады и соответствующие им восьмеричные цифры. Старшая триада получилась неполной. Её нужно дополнить старшими незначащими нулями для того, чтобы можно было бы воспользоваться таблицей 2.1.

Глава 3

Преобразование дробной части числа

Так как дробная часть числа меньше единицы, то её преобразование выполняется умножением исходного числа на основание новой системы счисления. Целая часть результата умножения будет старшим разрядом числа в новой системе счисления. Дробную часть произведения снова умножают на основание системы счисления. Операция умножения выполняется до достижения требуемой точности результата. Все операции выполняют по правилам исходной системы счисления.

Для примера рассмотрим перевод дробного числа из десятичной системы счисления в двоичную. Пусть исходное число A будет равно 0,35. Выполним операцию последовательного умножения, как это показано на рисунке 3.1.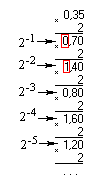

 
Рисунок 3.1. Пример операции последовательного умножения для перевода дробного числа в двоичную систему счисления

В результате преобразования получим двоичное представление числа A:

A = 0,35₁₀ = 0,01011

В общем случае перевод правильных дробей является бесконечным. Число разрядов в новой системе можно найти исходя из одинаковой точности представления чисел в разных системах счисления.

Одинаковая точность числа, записанного в различных системах счисления, достигается при одинаковых весах младших разрядов соответствующей системы счисления. Определить вес младшего разряда числа можно по следующей формуле:

M = q^–n

где q — основание системы счисления.

Определим необходимое число разрядов в двоичной системе счисления для рассмотренного ранее примера. Для десятичного числа 0.35 вес младшего разряда M = 1/100 = 0.01.

Раздел 4

Комбинационные устройства.

Глава 1

Законы алгебры логики

Законы алгебры логики базируются на аксиомах и позволяют преобразовывать логические функции. Логические функции преобразуются с целью их упрощения, а это ведет к упрощению цифровой схемы.

АКСИОМЫ алгебры логики описывают действие логических функций "И" и "ИЛИ" и записываются следующими выражениями:

0 * 0 = 0 0 * 1 = 0 1 * 0 = 0 1 * 1 = 1

0 + 0 = 0 0 + 1 = 1 1 + 0 = 1 1 + 1 = 1

Всего имеется пять законов алгебры логики:

1. Закон одинарных элементов

1 * X = X
0 * X = 0
1 + X = 1
0 + X = X

Этот закон непосредственно следует из приведённых выше выражений аксиом алгебры логики.

Верхние два выражения могут быть полезны при построении коммутаторов, ведь подавая на один из входов элемента “2И” логический ноль или единицу можно либо пропускать сигнал на выход, либо формировать на выходе нулевой потенциал.

Второй вариант использования этих выражений заключается в возможности избирательного обнуления определённых разрядов многоразрядного числа. При поразрядном применении операции "И" можно либо оставлять прежнее значение разряда, либо обнулять его, подавая на соответствующие разряды единичный или нулевой потенциал. Например, требуется обнулить 6, 3 и 1 разряды. Тогда: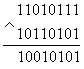



В приведённом примере отчётливо видно, что для обнуления необходимых разрядов в маске (нижнее число) на месте соответствующих разрядов записаны нули, в остальных разрядах записаны единицы. В исходном числе (верхнее число) на месте 6 и 1 разрядов находятся единицы. После выполнения операции "И" на этих местах появляются нули. На месте третьего разряда в исходном числе находится ноль. В результирующем числе на этом месте тоже присутствует ноль. Остальные разряды, как и требовалось по условию задачи, не изменены.

Точно так же можно записывать единицы в нужные нам разряды. В этом случае необходимо воспользоваться нижними двумя выражениями закона одинарных элементов. При поразрядном применении операции "ИЛИ" можно либо оставлять прежнее значение разряда, либо обнулять его, подавая на соответствующие разряды нулевой или единичный потенциал. Пусть требуется записать единицы в 7 и 6 биты числа. Тогда:

Здесь в маску (нижнее число) мы записали единицы в седьмой и шестой биты. Остальные биты содержат нули, и, следовательно, не могут изменить первоначальное состояние исходного числа, что мы и видим в результирующем числе под чертой.

Первое и последнее выражения позволяют использовать логические элементы с большим количеством входов в качестве логических элементов с меньшим количеством входов. Для этого неиспользуемые входы в схеме "И" должны быть подключены к источнику питания, как это показано на рисунке 1.1:

 
Рисунок 1.1. Схема "2И-НЕ", реализованная на логическом элементе "3И-НЕ"

а неиспользуемые входы в схеме "ИЛИ" должны быть подключены к общему проводу схемы, как это показано на рисунке 1.2.

 
Рисунок 1.2. Схема "НЕ", реализованная на элементе "2И-НЕ"

2. Законы отрицания

a. Закон дополнительных элементов

 

Выражения этого закона широко используется для минимизации логических схем. Если удаётся выделить из общего выражения логической функции такие подвыражения, то можно сократить необходимое количество входов элементов цифровой схемы, а иногда и вообще свести всё выражение к логической константе.

b. Двойное отрицание

   

c. Закон отрицательной логики

Закон отрицательной логики справедлив для любого числа переменных. Этот закон позволяет реализовыватьлогическую функцию "И" при помощи логических элементов "ИЛИ" и наоборот: реализовывать логическую функцию "ИЛИ" при помощи логических элементов "И". Это особенно полезно в ТТЛ схемотехнике, так как там легко реализовать логические элементы "И", но при этом достаточно сложно логические элементы "ИЛИ". Благодаря закону отрицательной логики можно реализовывать элементы "ИЛИ" на логических элементах "И". На рисунке 1.3 показана реализация логического элемента "2ИЛИ" на элементе "2И-НЕ" и двух инверторах.

 
Рисунок 1.3. Логический элемент "2ИЛИ", реализованный на элементе "2И-НЕ" и двух инверторах

То же самое можно сказать и о схеме монтажного "ИЛИ". В случае необходимости его можно превратить в монтажное "И", применив инверторы на входе и выходе этой схемы.

3. Комбинационные законы

Комбинационные законы алгебры логики во многом соответствуют комбинационным законам обычной алгебры, но есть и отличия.

a. закон тавтологии (многократное повторение)

X + X + X + X = X
X * X * X * X = X

Этот закон позволяет использовать логические элементы с большим количеством входов в качестве логических элементов с меньшим количеством входов. Например, можно реализовать двухвходовую схему "2И" на логическом элементе "3И", как это показано на рисунке 1.4:

 
Рисунок 1.4. Схема "2И-НЕ", реализованная на логическом элементе "3И-НЕ"

или использовать схему "2И-НЕ" в качестве обычного инвертора, как это показано на рисунке 1.5:

 
Рисунок 1.5. Схема "НЕ", реализованная на логическом элементе "2И-НЕ"

Однако следует предупредить, что объединение нескольких входов увеличивает входные токи логического элемента и его ёмкость, что увеличивает ток потребления предыдущих элементов и отрицательно сказывается на быстродействии цифровой схемы в целом.

Для уменьшения числа входов в логическом элементе лучше воспользоваться законом одинарных элементов, как это было показано выше.

b. закон переместительности

A + B + C + D = A + C + B + D

c. закон сочетательности

A + B + C + D = A + (B + C) + D = A + B + (C + D)

d. закон распределительности

X1(X2 + X3) = X1X2 + X1X3 X1 + X2X3 = (X1 + X2)(X1 + X3) = /докажем это путём раскрытия скобок/ =
= X1X1 + X1X3 + X1X2 + X2X3 = X1(1 + X3 + X2) + X2X3 = X1 + X2X3

4. Правило поглощения (одна переменная поглощает другие)

X1 + X1X2X3 =X1(1 + X2X3) = X1

5. Правило склеивания (выполняется только по одной переменной)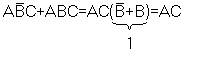

Также как в обычной математике в алгебре логики имеется старшинство операций. При этом первым выполняется:

1. 
   Действие в скобках
   
2. 
   Операция с одним операндом (одноместная операция) — "НЕ"
   
3. 
   Конъюнкция — "И"
   
4. 
   Дизъюнкция — "ИЛИ"
   
5. 
   Сумма по модулю два.
   

Операции одного ранга выполняются слева направо в порядке написания логического выражения. Алгебра логики линейна и для неё справедлив принцип суперпозиции.

Глава 2

Синтез цифровых комбинационных схем по произвольной таблице истинности

Любая цифровая комбинационная схема (логическая схема без памяти) полностью описывается таблицей истинности. При этом не обязательно чтобы все комбинации входных цифровых сигналов были полезными. Возможна ситуация, когда только часть комбинаций входных логических сигналов является полезной. В этом случае выходные сигналы цифрового устройства для оставшихся комбинаций входных логических сигналов могут быть доопределены произвольно. Обычно при этом стараются выбирать цифровые значения выходных сигналов таким образом, чтобы схема цифрового устройства получилась простейшей.

Для реализации цифровых логических схем с произвольной таблицей истинности используется сочетание простейших логических элементов "И" "ИЛИ" "НЕ". Существует два способа синтеза цифровых схем, реализующих произвольную таблицу истинности. Это СКНФ (логическое произведение суммы входных сигналов) и СДНФ (сумма логических произведений входных сигналов).

При синтезе цифровой схемы, реализующей произвольную таблицу истинности, каждый выход анализируется (и строится схема) отдельно и независимо. В настоящее время наиболее распространены цифровые микросхемы, совместимые с ТТЛ технологией, а в этой технологии производства микросхем проще всего получить логические элементы "И". Поэтому первым рассмотрим способ реализации произвольной таблицы истинности основанный на СДНФ.

Совершенная дизъюктивная нормальная форма (СДНФ)

Для реализации таблицы истинности при помощи логических элементов "И" (СДНФ) достаточно рассмотреть только те строки таблицы истинности, которые содержат логические "1" в выходном сигнале. Строки, содержащие в выходном сигнале логический 0 в построении цифровой схемы не участвуют. Каждая строка, содержащая в выходном сигнале логическую "1", реализуется схемой логического элемента "И" с количеством входов, совпадающим с количеством входных сигналов в таблице истинности.

Входные сигналы, описанные в таблице истинности логической единицей, подаются на вход этого логического элемента непосредственно, а входные сигналы, описанные в таблице истинности логическим нулем, подаются на вход этого же логического элемента "И" через инверторы. Объединение сигналов с выходов логических элементов "И", реализующих отдельные строки таблицы истинности, производится при помощи логического элемента "ИЛИ". Количество входов в логическом элементе "ИЛИ" определяется количеством строк в таблице истинности, в которых в выходном сигнале присутствует логическая единица.

Рассмотрим конкретный пример. Пусть необходимо реализовать таблицу истинности, приведенную на рисунке 2.1: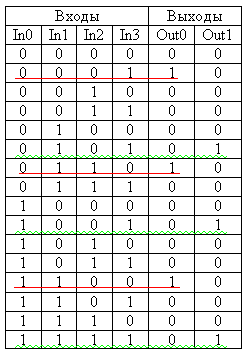



Рисунок 2.1. Произвольная таблица истинности.

Для синтеза цифровой схемы, реализующей сигнал Out0, достаточно рассмотреть строки, выделенные красным цветом. В таблице истинности три строки, содержащие единицу в выходном сигнале Out0, поэтому в формуле СДНФ будет содержаться три произведения входных сигналов — термов, а точнее минтермов:



Так как количество переменных в каждом терме (ранг терма) данного логического выражения равно, то такое логическое выражение называется совершенным. (Совершенная Дизъюнктивная Нормальная Форма — СДНФ)

Полученное логическое выражение реализуются микросхемой D2 в схеме, приведенной на рисунке 2. Как и в формуле, каждая строка (терм) реализуется своим логическим элементом "И", затем выходы этих логических элементов объединяются при помощи логического элемента "ИЛИ". Количество входов логического элемента "И" (дизъюнкция) в СДНФ однозначно определяется количеством входных сигналов в таблице истинности. Количество этих элементов, а значит и количество входов в логическом элементе "ИЛИ" определяется количеством строк с единичным сигналом на реализуемом выходе цифровой схемы.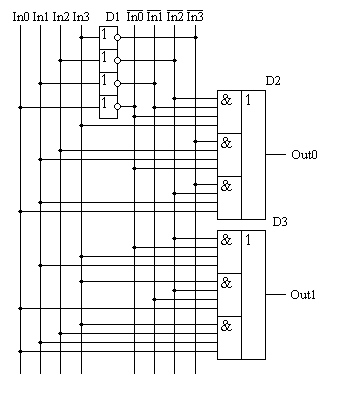

 
Рисунок 2.2 Принципиальная схема, реализующая таблицу истинности, приведенную на рисунке 2.1.

Для построения схемы, реализующей сигнал Out1, достаточно рассмотреть строки, выделенные зеленым цветом. Эти строки реализуются микросхемой D3. Принцип построения этой схемы не отличается от примера, рассмотренного выше. В таблице истинности присутствуют всего три строки, содержащие единицу в выходном сигнале Out1, поэтому в формуле СДНФ выхода Out1 будет содержаться три произведения входных сигналов:



Обычно при построении цифровых схем после реализации таблицы истинности производится минимизация схемы, но для упрощения понимания материала сейчас минимизация производиться не будет. Это оправдано еще и с той точки зрения, что неминимизированные схемы обычно обладают максимальным быстродействием. При реализации схемы на ТТЛ микросхемах быстродействие всего узла будет равно быстродействию одиночного инвертора (см. описание ТТЛ микросхем).

По СДНФ форме логического выражения обычно строятся современные микросхемы большой интеграции — программируемые логические интегральные схемы (ПЛИС), такие как программируемые логические матрицы (ПЛМ), программируемые матрицы логики ПМЛ или CPLD.

Совершенная конъюктивная нормальная форма (СКНФ)

Еще одним способом реализации цифровых комбинационных схем является запись логического выражения в совершенной конъюктивной нормальной форме (СКНФ). Применение СКНФ оправдано при большом количестве логических единиц в выходном сигнале проектируемой цифровой схемы, как это показано в качестве примера в таблице истинности 2, или в ЭСЛ-микросхемах.

Таблица 2.2 Пример таблицы истинности 2.2

№ комбинации	Входы				Выходы
	8	4	2	1	A	b
0	0	0	0	0	1	1
1	0	0	0	1	0	1
2	0	0	1	0	1	1
3	0	0	1	1	1	1
4	0	1	0	0	0	1
5	0	1	0	1	1	0
6	0	1	1	0	1	0
7	0	1	1	1	1	1
8	1	0	0	0	1	1
9	1	0	0	1	1	1

Для реализации цифрового комбинационного устройства по таблице истинности при помощи логических элементов "ИЛИ" (СКНФ) достаточно рассмотреть только те строки таблицы истинности, которые содержат логические "0" в выходном сигнале. Строки, содержащие в выходном сигнале логическую "1" в построении логического выражения, а, следовательно, и принципиальной схемы цифрового устройства не участвуют. Каждая строка, содержащая в выходном сигнале логический "0", реализуется схемой логического элемента "ИЛИ" с количеством входов, совпадающим с количеством входных сигналов в таблице истинности.

Для построения схемы, реализующей сигнал Out0, достаточно рассмотреть строки, выделенные курсивом. В рассматриваемой таблице истинности имеются всего две строки, содержащие логический ноль в выходном сигнале a, поэтому в формуле СКНФ будет содержаться две суммы входных сигналов:



Входные сигналы, описанные в таблице истинности логическим нулём, подаются на вход этой схемы непосредственно, а входные сигналы, описанные в таблице истинности логической единицей, подаются на логического элемента "ИЛИ" через инверторы. Объединение сигналов с выходов схем "ИЛИ", реализующих отдельные строки таблицы истинности, производится при помощи схемы логического элемента "И". Количество входов в схеме "И" определяется количеством строк в таблице истинности, в которых в выходном сигнале присутствует логическая единица.

Полученная формула в схеме на рисунке 9 реализуются микросхемой D2.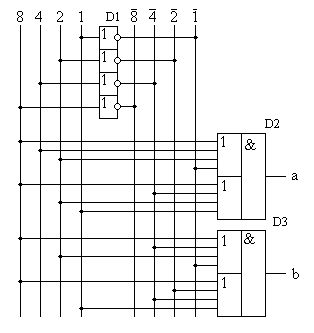



Для построения схемы, реализующей сигнал b, достаточно рассмотреть строки, выделенные жирным шрифтом. Эти строки в схеме на рисунке 9 реализуются микросхемой D3. Принцип построения этой схемы не отличается от примера, рассмотренного выше. В таблице истинности присутствуют всего две строки, содержащие ноль в выходном сигнале b, поэтому в формуле СКНФ выхода b будет содержаться две суммы входных сигналов: