Билеты. Позиционные системы счисления (с основанием 2,8,10,16,n) Преобразование из одной системы в другую. Выполнение арифметических операций
 Скачать 4.45 Mb.
|
|
Позиционные системы счисления (с основанием 2,8,10,16,n) Преобразование из одной системы в другую. Выполнение арифметических операций. Позиционные системы счисления — это системы счисления, в которых значение цифры напрямую зависит от её положения в числе. Например, число 01 обозначает единицу, 10 — десять Для составления машинных кодов удобно использовать не десятичную, а двоичную систему счисления, содержащую только две цифры, 0 и 1. Обратите внимание, что в двоичной системе максимальная цифра 1. Программисты для вычислений также пользуются ещё восьмеричной и шестнадцатеричной системами счисления. Количество цифр, используемых в системе счисления, называется её «основанием». В десятичной системе основание равно десяти, в двоичной системе — двум, ну а в восьмеричной и шестнадцатеричной — соответственно, восьми и шестнадцати. То есть в р-ичной системе счисления количество цифр равно р и используются цифры от 0 до р-1. 1. Для перевода двоичного числа в десятичное  При переводе удобно пользоваться таблицей степеней двойки:
Пример . Число  перевести в десятичную систему счисления. 2. Для перевода восьмеричного числа в десятичное  При переводе удобно пользоваться таблицей степеней восьмерки:
Пример . Число  перевести в десятичную систему счисления.  3. Для перевода шестнадцатеричного числа в десятичное  При переводе удобно пользоваться таблицей степеней числа 16:
Пример . Число  перевести в десятичную систему счисления.  4. Для перевода десятичного числа в двоичную систему Пример. Число 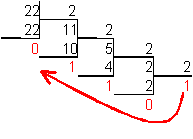 перевести в двоичную систему счисления.  5. Для перевода десятичного числа в восьмеричную Пример. Число 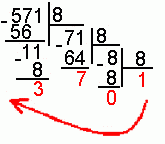 перевести в восьмеричную систему счисления.  6. Для перевода десятичного числа в шестнадцатеричную Пример. Число 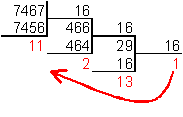 перевести в шестнадцатеричную систему счисления.   7. Чтобы перевести число из двоичной системы в восьмеричную, его нужно разбить на триады (тройки цифр) Пример. Число  перевести в восьмеричную систему счисления.  8. Чтобы перевести число из двоичной системы в шестнадцатеричную, его нужно разбить на тетрады (четверки цифр) Пример. Число 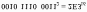 перевести в шестнадцатеричную систему счисления.  9. Для перевода восьмеричного числа в двоичное необходимо каждую цифру заменить эквивалентной ей двоичной триадой. Пример. Число  перевести в двоичную систему счисления.  10. Для перевода шестнадцатеричного числа в двоичное необходимо каждую цифру заменить эквивалентной ей двоичной тетрадой. Пример. Число  перевести в двоичную систему счисления.  11. При переходе из восьмеричной системы счисления в шестнадцатеричную и обратно, необходим промежуточный перевод чисел в двоичную систему. Пример 1. Число  перевести в восьмеричную систему счисления. Пример 2. Число  перевести в шестнадцатеричную систему счисления. 0x – шестнадцатиричная – hex Восьмеричная –oct Десятичная - dec Переводим целую часть 123410 в 5-ую систему последовательным делением на 5: 1234/5=246,остаток:4 246/5=49,остаток:1 49/5=9,остаток:4 9/5=1,остаток:4 1/5=0,остаток:1 123410 = 144145 Переводим 1110012 в десятичную систему: 1110012 = 1·25+1·24+1·23+0·22+0·21+1·1 = 5710 Переводим целую часть 5710 в 3-ую систему последовательным делением на 3: 57/3 = 19, остаток: 0 19/3 = 6, остаток: 1 6/3 = 2, остаток: 0 2/3 = 0, остаток: 2 5710 = 20103 Переводим 125678 в десятичную систему: 125678 = 1·84+2·83+5·82+6·81+7·1 = 549510 Переводим целую часть 549510 в 7-ую систему последовательным делением на 7: 5495/7 = 785, остаток: 0 785/7 = 112, остаток: 1 112/7 = 16, остаток: 0 16/7 = 2, остаток: 2 2/7 = 0, остаток: 2 549510 = 220107 Переводим AF116 в десятичную систему: AF116 = 10·162+15·161+1·1 = 280110 Переводим целую часть 280110 в 4-ую систему последовательным делением на 4: 2801/4 = 700, остаток: 1 700/4 = 175, остаток: 0 175/4 = 43, остаток: 3 43/4 = 10, остаток: 3 10/4 = 2, остаток: 2 2/4 = 0, остаток: 2 280110 = 2233014 Сложим числа 15 и 6 в различных системах счисления. Таблица сложения в восьмеричной системе: 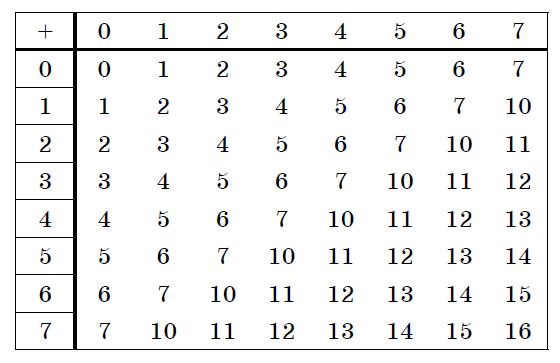 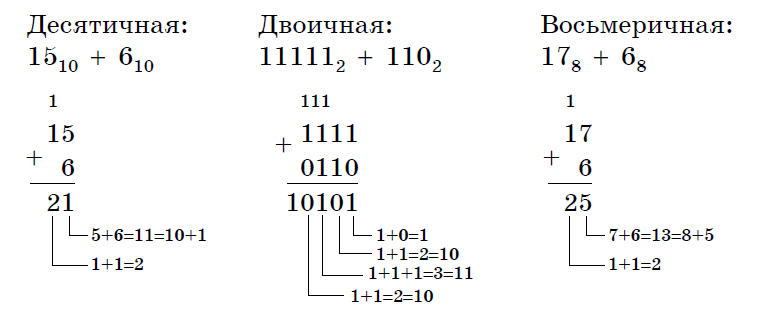 Ответ: 15+6=2110=101012=258 Разность 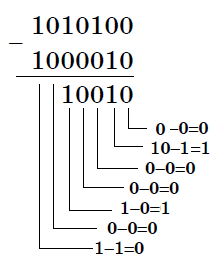 Ответ: 100102 Таблица умножения в восьмеричной системе: 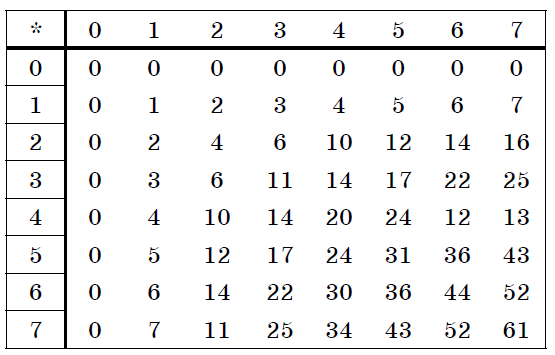 Перемножим числа 15 и 12.  Ответ: 15⋅12=18010=101101002=2648 форматы представления знаковых числе в двоичной системе счисления    Преобразование логических функций. Логические элементы. Реализация логических функций на логических элементах, в т.ч. в базисах И-НЕ и ИЛИ-НЕ.    Логические элементы — устройства, предназначенные для обработки информации в цифровой форме. 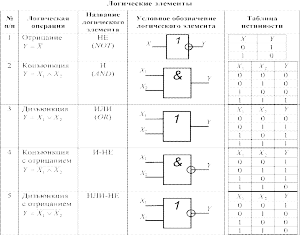 Вот три основных действия: AND. 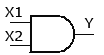 OR. 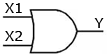 NOT.  NAND. 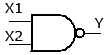 NOR. 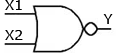 кружочек на выходе подразумевает инвертирование сигнала 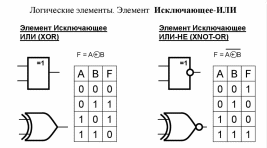 Логический элемент "исключающее ИЛИ".«неравнозначность» Высокий потенциал на выходе возникает только в том случае, если входные сигналы не равны. То есть на одном из входов должна быть единица, а на другом ноль. Если на выходе логического элемента имеется инвертор, то функция выполняется противоположная – «равнозначность». Высокий потенциал на выходе будет появляться при одинаковых сигналах на обоих входах. При реализации цифровых устройств на интегральных микросхемах широко используются базисы И-НЕ или ИЛИ-НЕ. Для этого минимизированные логические функции путем преобразований приводятся к соответствующему виду. Пусть минимальная ДНФ функция  .Применим к этому выражению двойное отрицание и теорему де Моргана  .Как видно, функция F включает только операции И-НЕ, и ее реализация в базисе И-НЕ имеет вид (рис. 8) 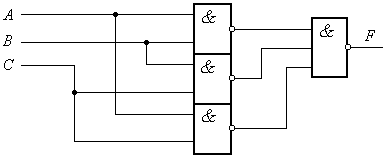 Рис. 8. Реализация функции  в базисе И-НЕАналогичным образом от КНФ функции можно перейти к ее форме, удобной для реализации в базисеИЛИ-НЕ Мультиплексоры. Условное графическое обозначение. Принцип работы .назначение выводов. Наращивание разрядности. 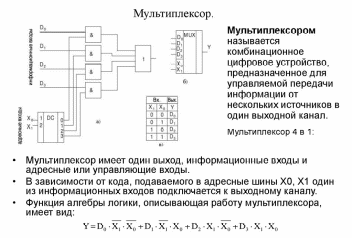 X1,X2 – Адресные входа(управляющие) (M) D1…D3 - коммутационные входа (N) M=2^N 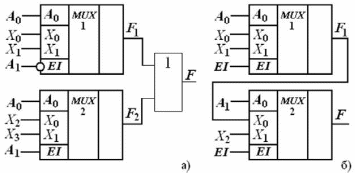 Рис. Увеличение разрядности,а – реализация MUX(4-1) на двух MUX(2-1),б – реализация MUX(3-1) на двух MUX(2-1) реализация логической функции на мультиплексоре Мультиплексоры удобно использовать для реализации логических функций, записанных непосредственно в СДНФ. Любую булеву функцию четырех переменных можно реализовать с помощью восьмиканального мультиплексора. Так, для реализации, например, логической функции   ,Где D – переменная младшего разряда, на адресные входы мультиплексора К555КП7 поданы входные сигналы А,В,С ,а входы Х0 – Х7 используются как настроечные. Сравнивая выражение для функции Fc логическим уравнением мультиплексора  получаем условия эквивалентности: X0 = X3 =  , X7 = D, X5 = + D =1, X1 = X2 = X4 = X6 = 0.Эти соотношения позволяют зашифровать входы мультиплексора на выполнение заданного логического уравнения. Для получения сигнала  использован инвертор.Демультиплексоры. Условное графическое обозначение. Принцип работы. Назначение выводов. Наращивание разрядности.  Демультиплексор — это логическое устройство, предназначенное для переключения сигнала с одного информационного входа на один из информационных выходов. Таким образом, демультиплексор в функциональном отношении противоположен мультиплексору. На схемах демультиплексоры обозначают через DMX или DMS. Демультиплексор можно построить на основе точно таких же схем логического "И", как и при построении мультиплексора. Существенным отличием от мультиплексора является возможность объединения нескольких входов в один без дополнительных схем. Однако для увеличения нагрузочной способности микросхемы, на входе демультиплексора для усиления входного сигнала лучше поставить инвертор. 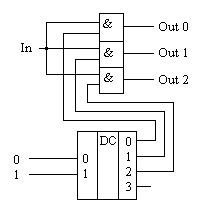 Рисунок 1. Принципиальная схема демультиплексора, управляемого двоичным кодом Повышение разрядности: 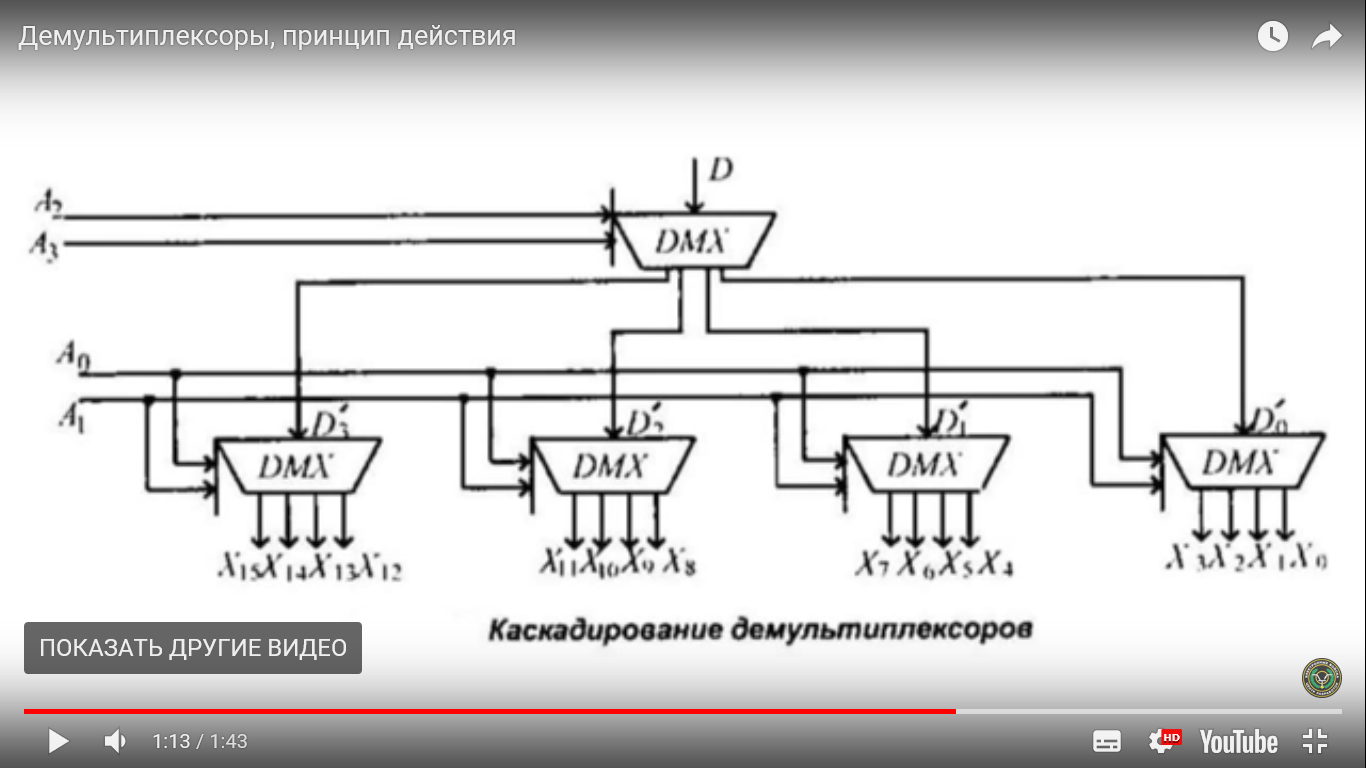 Шифраторы и дешифраторы. Условное графическое обозначение. Принцип работы. Назначение выводов. Наращивание разрядности. 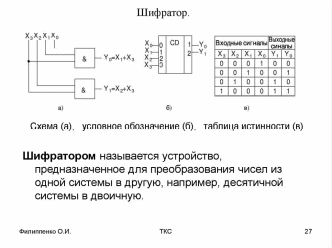 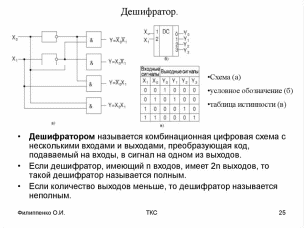 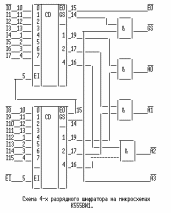 вход разрешения EI , выход разрешения Е0 и выход группового сигнала GS. Дополнительные выходы образуются с помощью дополнительных логических элементов. 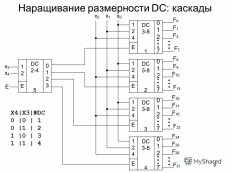 Арифметический компаратор. Условное графическое обозначение. Назначение выводов. Принцип работы. |
