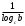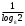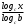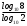Логарифмы. Самое важное!. Что такое логарифм и как его посчитать
 Скачать 0.51 Mb. Скачать 0.51 Mb.
|
Что такое логарифм и как его посчитатьЛогарифм имеет следующий вид:
Чтобы узнать значение логарифма приравняем его к X. Чтобы было легче, можно запоминать так – основание всегда остается внизу (и в первом, и во втором выражении a внизу)! Приведем пример: Чтобы вычислить данный логарифм, необходимо приравнять его к X и воспользоваться правилом, описанным выше: А в какую степень нужно возвести 2, чтобы получилось 8? Конечно же в третью степень, таким образом: 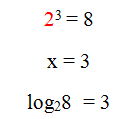 Запомним!!!  Таблица свойств логарифмов
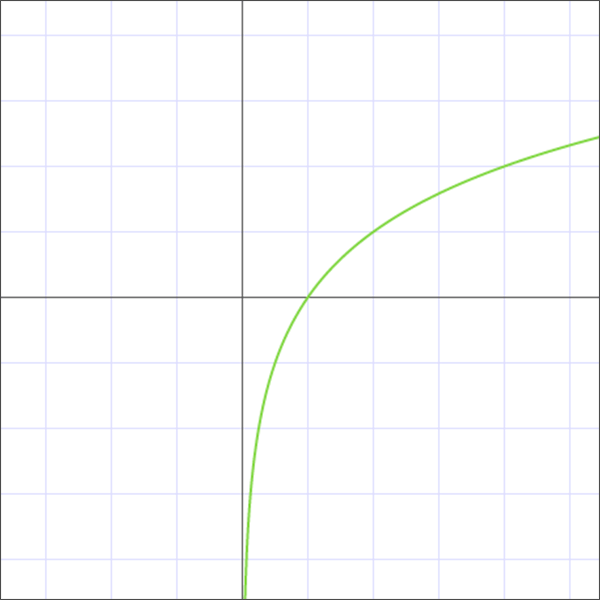
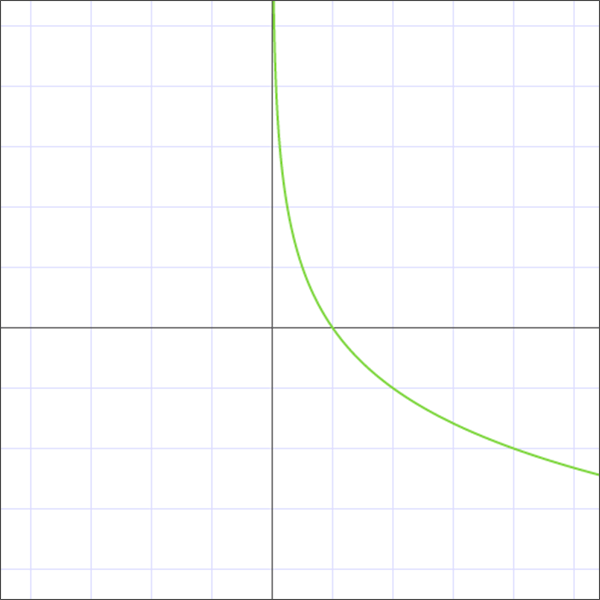
Логарифмическая функция Функция, которая определена формулой f(x)=loga(x) – это логарифмическая функция с основанием a. При этом a>0, a≠1. График функции логарифма График логарифмической функции (логарифмика) может быть двух типов, в зависимости от значения основания a:
Десятичный логарифмДесятичный логарифм обозначается lg и имеет основание 10, т.е. Например, вычислим lg100 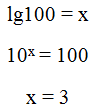 Натуральный логарифмНатуральный логарифм обозначается ln и имеет основание e, то есть Чтобы вычислить данный логарифм нужно число е возвести в степень x. Некоторые из вас спросят, что это за число такое е? Число е – это иррациональное число, т.е. точное его значение вычислить невозможно. е = 2,718281… Сейчас не будем подробно разбирать, зачем это число нужно, просто запомним, что И вычислить его можно таким образом: 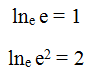 Задания для подготовки к ЕГЭ 1. Задание 9 № 26646 Найдите корень уравнения
Ответ: −124. 2. Задание 9 № 26647 Найдите корень уравнения
Ответ: 21. 3. Задание 9 № 26648 Найдите корень уравнения
Ответ: 2. 4. Задание 9 № 26649 Найдите корень уравнения
Ответ: −12. 5. Задание 9 № 26657 Найдите корень уравнения Решение. Логарифмы двух выражений равны, если сами выражения равны и при этом положительны:
Ответ: 6. 6. Задание 9 № 26659 Найдите корень уравнения
Ответ: −4. 7. Задание 9 № 77381 Решите уравнение Решение. Заметим, что
Ответ: 2. 8. Задание 9 № 509692 Найдите корень уравнения
Ответ: 22,4. 9. Задание 9 № 512584 Найдите корень уравнения Решение. Логарифмы выражений равны, если сами выражения равны и при этом положительны:
Ответ: 3. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

 ) = logb x - logb y
) = logb x - logb y ) = log103 - log107
) = log103 - log107