Цифровыеустройства. Технология idl

• Название: Цифровыеустройства. Технология idl
• Дата: 15.02.2022
• Размер: 3.16 Mb.
• Имя файла: Budko_CU.docx
• Тип: Документы; #362193
• страница: 37 из 46

Исследование счетчика Джонсона

1. 
   На основе регистра сдвига (см.рис. 7.5) построить счетчик Джонсона. Для построения счетчика Джонсона необходимо соединить ин- версный выход 0Qс последовательным входом регистра.
   
2. 
   Для исследования работы счетчика Джонсона вначале обнулить регистр, а затем подать синхроимпульсы. Результаты наблюдений табулиро- вать (см. табл. 7.1).
   
3. 
   Построить временные диаграммы работы счетчика Джонсона, сделать выводы.
   

1. 
   Цель работы.
   

3. 
   СОДЕРЖАНИЕ ОТЧЕТА
   

2. 
   Схемы исследуемых в работе устройств.
   
3. 
   Таблицы и временные диаграммы,отражающие результаты иссле- дований.
   
4. 
   Выводы по результатам исследований.
   

4. 
   КОНТРОЛЬНЫЕ ВОПРОСЫ
   

1. Объяснить работу регистров во всех четырех режимах работы. 2 . Как строится реверсивный регистр сдвига?

3. 
   . Как строится кольцевой счетчик?
   
4. 
   . Чему равен модуль счета кольцевого счетчика? 5 . Как строится счетчик Джонсона?
   

6 .Чему равен модуль счета счетчика Джонсона?

Лабораторная работа №8

ГЕНЕРАТОРЫ ПОСЛЕДОВАТЕЛЬНОСТЕЙ

Цельработы:

1. 
   Изучение синтеза генераторов последовательностей.
   
2. 
   Исследование работы генераторов последовательностей.
   

1. 
   ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ
   

Схема, которая генерирует заданную последовательность бит синхрон- но с импульсами синхронизации, называется генератором последовательно- стей. Такие генераторы используются как:

• 
  счетчики;
  
• 
  генераторы псевдослучайных последовательностей;
  
• 
  генераторы заданной последовательности и заданного периода;
  
• 
  генераторы кодов.
  

Генераторы последовательностей являются одним из наиболее инте- ресных применений регистров сдвига. Блок-схема генератора последователь- ностей приведена на рис. 8.1.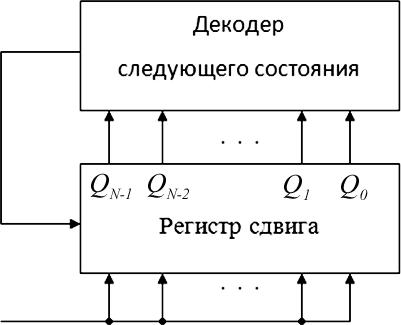



Рис. 8.1. Блок-схема генератора последовательностей
Выход декодера следующего состояния Y– это функция от Q_N-1, Q_N-2, … ,

Q₀, т. е. Y

f_(Q_n

1^,Qn

2. 
   ,...,Q₀ ) . Это схема подобна схеме кольцевого счет-
   

чика (Y=Q₀) или счетчика Джонсона ( Y Q₀ ). Кольцевой счетчик и счетчик

Джонсона являются частными случаями генераторов последовательностей.

Синтез генераторов последовательностей рассмотрим на примерах.

Пример 8.1. Синтезировать генератор следующей последовательности

… 1101011 … .

Решение. При синтезе генератора заданной последовательности необ- ходимо определить число разрядов регистра сдвига и комбинационную схе- му декодера следующего состояния.

Минимально возможное число триггеров Nв регистре сдвига для гене- рирования последовательности длиной S бит определяется из того, что
NSlog ₂ ( 1) . (8.1)
В данном примере S=7, поэтому минимально возможное значение N=3.

Однако это не значит, что это число триггеров является достаточным. Если данная последовательность ведет к семи различным состояниям регистра, то тогда три триггера будет достаточно, в противном случае число триггеров придется увеличить. Запишем состояние регистра в виде табл. 8.1.
Таблица 8.1

Число синхроимпульсов	Выходы триггеров
	Q2	Q1 Q	0
1	1	1	1
2	1	1	1
3	0	1	1
4	1	0	1
5	0	1	0
6	1	0	1
7	1	1	0

Допускаем, что данная последовательность генерируется на выходе Q₂. В таком случае на выходах Q₁ и Q₀ будет та же последовательность, только задержанная на один и два такта соответственно. Из табл. 8.1 видно, что не все состояния регистра отличаются от других (первая и вторая строки одина- ковы, а также четвертая и шестая). Это означает, что число триггеров регист- ра N=3 не является достаточным. Поэтому примем число N=4 и построим таблицу,аналогичную табл. 8.2.

Поскольку в данном случае все состояния регистра являются отличны- ми (разными),добавим в эту таблицу колонку,в которой запишем требуемую последовательность на входе регистра – Y.

Таблица 8.2

Число синхроимпульсов	Выходы триггеров					Y
	Q3	Q2 Q	1 Q	0
1	1	1	1	0	1
2	1	1	1	1	0
3	0	1	1	1	1
4	1	0	1	1	0
5	0	1	0	1	1
6	1	0	1	0	1
7	1	1	0	1	1
8 (1)	1	1	1	0	1

Схему декодера получим, упрощая функцию Y

мощью карты Карно (табл. 8.3).

f(Q₃ , Q₂ ,Q₁, Q₀ )

с по-

Q₃Q₂

Q₁Q₀

00

01

11

10
Таблица 8.3

X	X	X	X
X	1	1	X
X	1	0	1
X	X	0	1

00 01 11 10

Y Q₃  Q₁  Q₀  .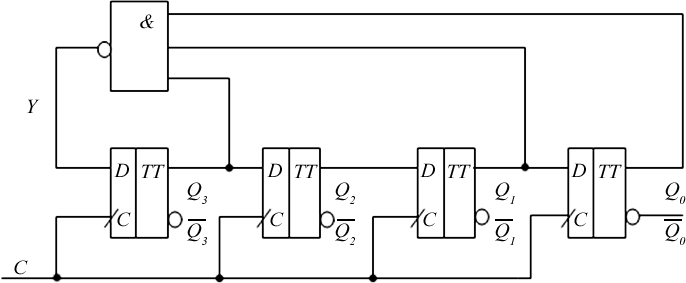
Упрощенная схема генератора последовательности … 1101011 … пока- зана на рис. 8.2

Рис. 8.2. Логическая структура генератора последовательности … 1101011 …

.

Пример 8.2. Синтезировать генератор последовательности … 1101001… .

Решение. Минимально возможное число триггеров регистра N=3.Проверим, является ли это число достаточным. Для этого построим табл. 8.4.
Таблица 8.4

Импульсы син- хронизации	Выходы триггеров			Y
	Q2 Q	1 Q	0
1	1	1	1	0
2	0	1	1	0
3	0	0	1	1
4	1	0	0	0
5	0	1	0	1
6	1	0	1	1
7	1	1	0	1

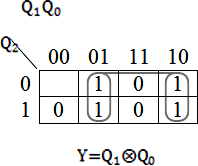Из табл. 8.4 видно, что все состояния регистра являются неодинаковы- ми,т.е.число триггеровN=3 является достаточным для реализации генератора. Поэтому добавим в эту таблицу колонку с требуемой на входе регистра последовательностью. Схему декодера получим, упрощая функцию

Y f(Q₂ ,Q₁ , Q₀ ) с помощью карты Карно.

На рис. 8.3 показана упрощенная схема генератора последовательности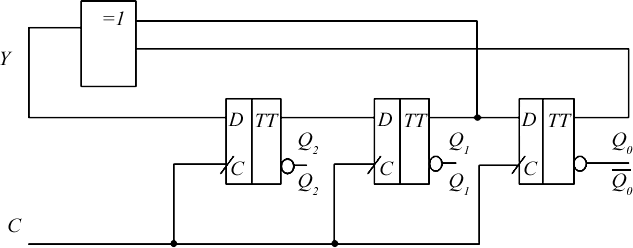

… 1101001… .

Рис. 8.3. Логическая структура генератора последовательности … 1101001

равна

Длина последовательности, генерируемой генератором (см. рис. 8.3),

S 2 ^N1  2³ 1  7 .

Генераторы, которые генерируют последовательности длиной

S2^N

1, (8.2)

называются генераторами последовательностей максимальной длины. Такие генераторы широко используются для генерирования помехоустойчивых ко- дов.

2. 
   ПОРЯДОК ВЫПОЛНЕНИЯ ЛАБОРАТОРНОЙ РАБОТЫ
   

Оборудование и компоненты: универсальная лабораторная установка IDL-800; ИС 1533ИР16 (74АLS295) – четырехразрядный регистр сдвига; ИС 1533ЛА4 (74ALS10) – три логических элемента 3И-НЕ; ИС 1533ЛП5 (74ALS86) – четыре двухвходовых логических элемента ИСКЛЮЧАЮЩЕЕ ИЛИ.