Цифровыеустройства. Технология idl

• Название: Цифровыеустройства. Технология idl
• Дата: 15.02.2022
• Размер: 3.16 Mb.
• Имя файла: Budko_CU.docx
• Тип: Документы; #362193
• страница: 2 из 46

ИССЛЕДОВАНИЕ ЛОГИЧЕСКИХ ЭЛЕМЕНТОВ

Цельработы:

1. 
   Изучение базовых логических функций.
   
2. 
   Исследование функционирования основных логических элементов.
   

1. 
   1. ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ
   

Все цифровые устройства построены на элементах, которые выполня- ют те или иные логические операции. Для анализа и синтеза цифровых уст- ройств используется аппарат алгебры логики. В общем случае цифровые уст- ройства разделяются на два типа:

− комбинационные;

− последовательностные.

В комбинационных устройствах выходной сигнал в любой момент времени зависит только от значений входных сигналов в тот же момент вре- мени.

В последовательностных устройствах выходной сигнал в любой мо- мент времени зависит как от значений входных сигналов в данный момент времени, так и от значений входных сигналов в предыдущие моменты време- ни. Для этого эти устройства имеют память. В последовательностных уст- ройствах комбинационные устройства являются составной частью, поэтому комбинационные устройства изучаются первыми.

Рассмотрим комбинационное устройство,блок-схема которого показа- на на рис. 1.1.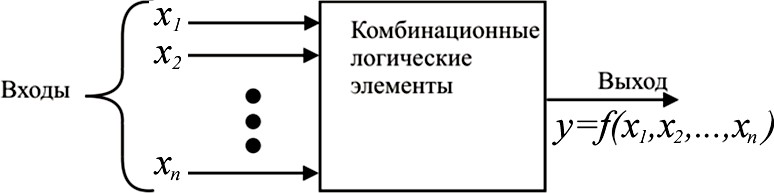




Рис. 1.1. Блок-схема комбинационного устройства Входные и выходные сигналы комбинационного устройства могут

принимать только два логических значения 0 или 1, т. е.

0,1x_i.

0,1; y_i

Любая совокупность входных сигналов может быть представлена вектором

, , Х, х₁ х₂  х_п

и называется входным набором.

Очевидно, что существует

2 ^празличных входных наборов. Сопоста-

вим каждому входному набору определенное значение выходного сигнала

, х₁fу,х_2,  х_п. Тогда работа комбинационной схемы (устройства) может

быть описана с помощью функции, отображающей множество входных на- боров в значение выходной переменной Y.

Определение. Функцией алгебры логики (ФАЛ), хf,₁ х_2,  х_п называ-

ется функция, дающая однозначное отображение множества векторов Хв пе- ременную Y.

Так как число различных входных наборов равно

2^п, то любая ФАЛ

может быть задана в виде таблицы со

2^пстроками (табл. 1.1).

Таблица 1.1

x1	x2	…	xn1	xn	f(x1,x2,…,xn)
0	0	…	0	0 α	1
0	0	…	0	1 α	2
0	0	…	1	0 α	3
...	…	…	…	…	…
1	1	…	0	0 α	2 3
1	1	…	0	1 α	2 2
1	1	…	1	0 α	2 1
1	1	…	1	1 α	2

В левой части таблицы перечислены все возможные входные наборы, а в правой записаны значения функции на этих наборах.

Каждая ФАЛ представляет собой двоичный набор длиной

2^п, а число

возможных таких наборов равно

2²п , поэтому справедливо следующее ут-

верждение : число различных функций алгебры логики, зависящих от nаргу-

ментов, конечно и равно

2²п .

Рассмотрим несколько примеров. Пустьn= 1, тогда число функций ал-

гебры логики

2²п = 4. Эти функции приведены в табл. 1.2.

Таблица 1.2

	f0	f1	f2	f3
0 1	0 0	0 1	1 0	1 1

Функции

f₀ и

f₃ − логические константы (константа нуля и константа

единицы). Функция

f₁ называется функцией тождества или просто тождеством,

т. к.

f₁ = х, а функция

f₂ называется функцией отрицания или просто отри-

цанием, f₃ ^х(читается «не Х»), функция НЕ.

Для 2 существует приведены в табл. 1.3.

₂₂п

₂₂2

16 функций алгебры логики, которые

Таблица 1.3

х1	х2	f0	f1	f2	f3	f4	f5	f6	f7	f8	f9	f10	f11	f12	f13	f14	f15
0	0	0	0	0	0	0	0	0	0	1	1	1	1	1	1	1	1
0	1	0	0	0	0	1	1	1	1	0	0	0	0	1	1	1	1
1	0	0	0	1	1	0	0	1	1	0	0	1	1	0	0	1	1
1	1	0	1	0	1	0	1	0	1	0	1	0	1	0	1	0	1
Опе- рац. символ									+ ↓							↑

Рассмотрим эти функции.

Функции ₀ хf₁,х₂  и ₁₅ хf₁,х₂  – логические константы. Функция

₀хf₁,х₂  0 ₁₅ хf₁,х₂  – константа нуль (функция нуль). Технически f₀

реализуется генератором нуля (рис. 1.1, а).

Функция ₁₅ хf₁,х₂  1 ₀ хf₁,х₂  – константа единица (функция еди-

ница). Технически реализуется генератором единицы (рис. 1.2, б).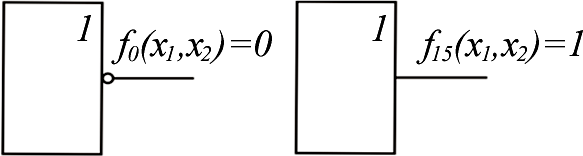




а б

Рис. 1.2. Условное обозначение генераторов логических констант Будем продолжать рассматривать функции в табл. 1.3 по парам, т. к. по

отношению к любой функции вторая функция в паре является инверсной.

Функция ₁хf₁,х₂  – конъюнкция, логическое умножение, функция И:

₁ ₁, ₂  хfxх₁ & x₂  x₁  x₂  x₁x₂  f₁₄ (x₁, x₂ ) .

Технически реализуется логическим элементом И,как показано на рис. 1.3, а.

Функция ₁₄ хf₁,х₂  – функция Шеффера, функция И-НЕ :

 f₁₄ (x₁, x₂ )


x₁x₂


f₁(x₁, x₂ ) .

Технически реализуется логическим элементом Шеффера, элементом И-НЕ, (рис. 1.3, б).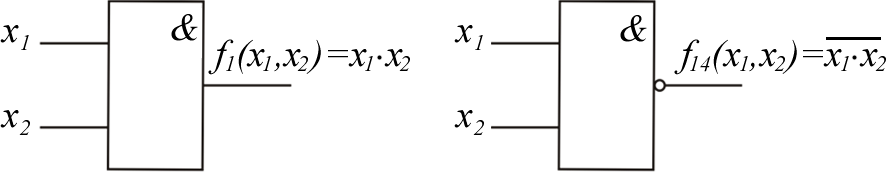



а б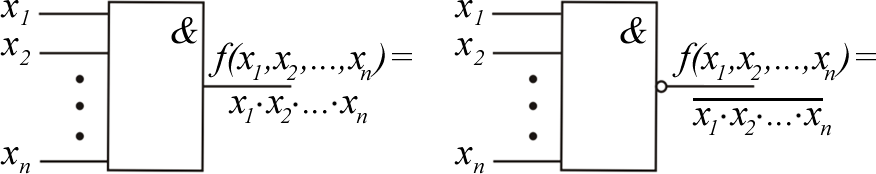




в г

Рис. 1.3. Условное обозначение логических элементов И и И-НЕ Функции И и И-НЕ могут быть, как и соответствующие им логические

элементы, с произвольным числом переменных (входов) (рис. 1.3, в, г).

Функция

f₂ – запрет 1-го аргумента :

f₂ (x₁, x₂ )  x₁  x₂

 x₁  x₂ 

f₁₃ (x₁, x₂ ) .

Технически реализуется элементом запрета (рис. 1. 4, а).

Функция

^f13

– импликация от 1-го аргумента ко второму :

( , f)₁₃

x₁ x₂  ₁

х₂

х₁ xх₂


f₂ (x₁, x₂ ) .

Технически реализуется импликатором (рис. 1. 4, б).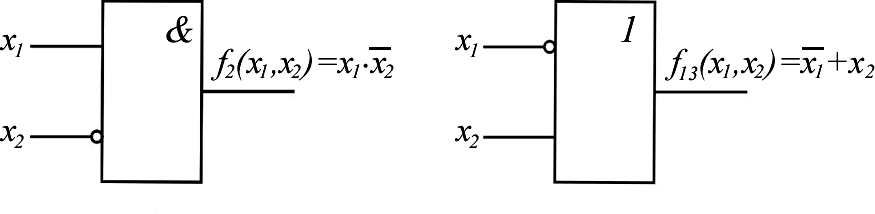




а б

Рис. 1.4. Условное обозначение:

а – элемента запрета; б – импликатора

Функция

f₃ – повторение первого аргумента (функция ДА):

 f₃ (x₁ , x₂ ) x₁ f₁₂ (x₁ , x₂ ) .

Технически реализуется повторителем(рис. 1. 5, а).

Функция

^f12

– отрицание первого аргумента (функция НЕ) :

^{f12 (x1, x2 ) x1 f3 (x1, x2 )} . ^

Технически реализуется инвертором (рис. 1. 5, б).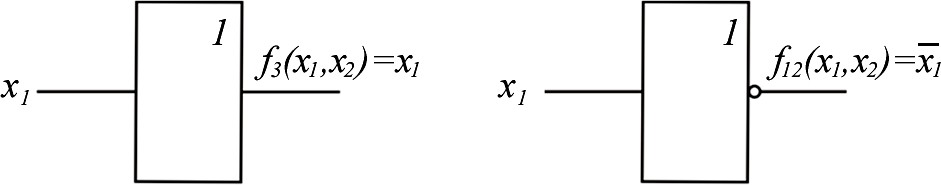




а б
Рис. 1.5. Условные обозначения повторителя и инвертора

Функция

f₄ – запрет 2-го аргумента :

f₄х₁,х₂   ₂  х₁

₁х₂ х

f₁х₁ х₁,х₂ .

Функция

f₁₁ – импликация от 2-го аргумента к 1-му :

f₁₁ х₁,х₂  ₂ х_{1 1}х₂хfх₄ х₁,х₂ .

Функция

f₅ – повторение 2-го аргумента :

f₅ х₁,х₂  = х₂ = ₁₀ хf₁,х₂ .

Функция

^f10

– отрицание второго аргумента :

f₁₀ х₁,х₂  = х₂ = ₅ хf₁,х₂ .

Функция

f₆ – неравнозначность, ИСКЛЮЧАЮЩЕЕ ИЛИ :

f₆ х₁,х₂   х₁  ₂  ₁х₂ х₁х₂ хfх₉ х₁,х₂ .

Технически реализуется логическим элементом «ИСКЛЮЧАЮЩЕЕ ИЛИ» (рис. 1. 6, a).

Функция

f₉ – равнозначность, эквивалентность, «ИСКЛЮЧАЮЩЕЕ ИЛИ-НЕ»:

f₉(x₁,x₂ ) x₁  x₂  x₁x₂  x₁  x₂  x₁  x₂ 

Технически реализуется элементом равнозначность,

«ИСКЛЮЧАЮЩЕЕ ИЛИ–НЕ» (рис.1.6, б).

f₆(x₁,x₂ ).

Функции неравнозначность и равнозначность могут быть, как и соот- ветствующие им логические элементы, с произвольным числом переменных (входов) (рис. 1.6, в, г). Функция неравнозначность равна 1, если число аргу- ментов, равных 1, нечетно.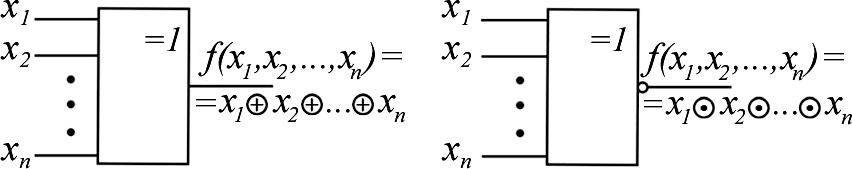

а б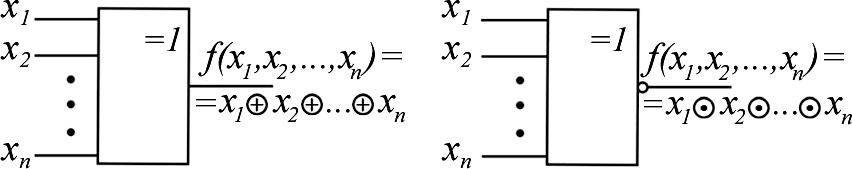




в г
Рис. 1.6.Логические элементы,реализующие функции неравнозначность и равнозначность

Функция

f₇ – дизъюнкция, функция ИЛИ :

  f₇ (x₁, x₂ )

x₁ x₂

f₈ (x₁, x₂ ) .

Технически реализуется элементом ИЛИ (рис. 1.7, а).

Функция

f₈ – функция Пирса или функция Вебба (функция ИЛИ-НЕ) :

  f₈ (x₁, x₂ )

x₁ x₂

f₇ (x₁, x₂ ) .

Технически реализуется элементом Пирса или Вебба (элемент ИЛИ-НЕ)

(рис.1. 7, б).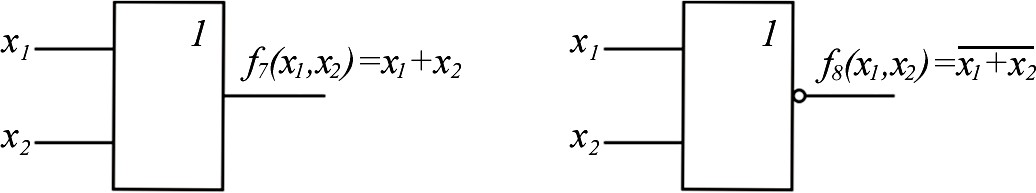



а б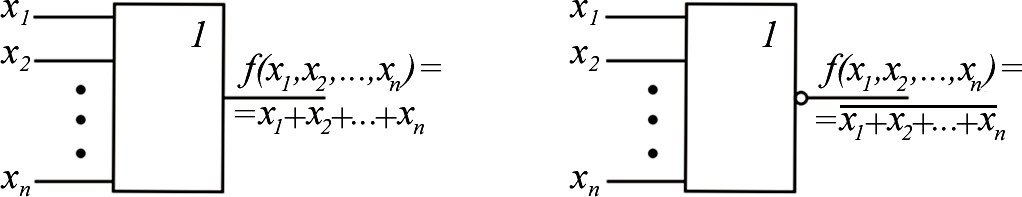




в г
Рис. 1.7. Логические элементы ИЛИ и ИЛИ-НЕ

Функции ИЛИ и ИЛИ-НЕ могут быть, как и соответствующее им логи- ческие элементы, с произвольным числом переменных (входов) (рис. 1.7, в, г). Значение функций двух переменных в общей теории логических функ-

ций состоит в том, что с их помощью может быть представлена любая сколь- ко угодно сложная ФАЛ.Средством для такого представления является су- перпозиция булевых функций или подстановка одних логических функций вместо аргументов в другие функции. Возможность такой подстановки обу- словливается тем, что в силу определения области значений функций и их аргументов совпадают.

Для выражения сложных логических функций достаточно использовать

не все элементарные функции, а только их некоторую часть, называемую ба- зисом или системой.

Система элементарных функций

F₁, F_2,

F_kназывается функциональ-

но полной, если любую функцию алгебры логики можно записать в виде

формулы через функции

F₁, F_2,

F_k.

Минимальным базисом называется такая функционально полная сис-

тема –

F₁, F_2,

^F_m^, для которой удаление любой одной из входящих в нее

функций превращает эту систему в функционально неполную.
Примерами полных систем являются:

1. F₁ х₁,х₂ 

х₁ х₂ ,

F₂ х₁,х₂ 

х₁  х₂ ,

F₃ х х.

2. F₁ х₁,х₂ 

х₁  х₂ ,

F₂ х х.

3. F₁ х₁,х₂ 

х₁ х₂ ,

F₂ х х.

4. Fх₁,х₂ 

5. Fх₁,х₂ 

х₁ х₂ .


х₁ х₂ .

6. F₁ х₁,х₂ 

х₁ х₂ ,

F₂ х₁,х₂ 

х₁  х₂ ,

F₃ х 1.

ФАЛ можно изменять, упрощать. Для проведения таких манипуляций используются основные законы алгебры логики, правила, теоремы упроще- ния, которые представлены в виде табл. 1.4.

Таблица 1.4

Основные законы,правила и теоремы алгебры логики

Для оператора (+)

Для оператора 

Переместительный закон (коммутативный)

х₁ х₂

х₂ х₁

х₁  х₂

х₂ х₁

Сочетательный закон (ассоциативный)

х₁  х₂   х₃

х₁  х₂  х₃ 

х₁  х₂ х₃

х₁х₂

х₃ 

Распределительный закон (дистрибутивный)

х₁  х₂

х₃ 

х₁х₂

х₁х₃

х₁ х₂  х₃

х₁

х₂  х₁

х₃ 

Закон отрицания (закон де Моргана)

  х₁ х₂

х₁ х₂


  х₁ х₂

х₁ х₂

х0 х

Операции с логической 1 и 0

х 0 0

1 1 х1 х

Правило повторения (идемпотентности)

хх


хх

Правило дополнительности

1

Правило двойного отрицания

хх



 хх
0

х

Теоремы

х

упрощения

 x₁x₂


x₁ x₂

x₁ 

x xxx

(x<sub>1

2</sub> )( ₁


2 ⁾ 1

 x₁( x₁

x₂ ) x₁

 x₁

x₁ x₂ x₁

 x₁(x₁

x₂ )

x₁x₂

  x₁

x₁x₂

x₁ x₂

2. 
   ПОРЯДОК ВЫПОЛНЕНИЯ ЛАБОРАТОРНОЙ РАБОТЫ
   

Оборудование и компоненты: универсальная лабораторная установка IDL-800; ИС 1533ЛА3(74АLS00) − четыре логических элемента 2И-НЕ; ИС 1533ЛЕ1(74АLS02) − четыре логических элемента 2ИЛИ-НЕ, ИС1533ЛН1(74 АLS04)− шесть логических элементов НЕ;

ИС 1533ЛИ1(74АLS08) − четыре логических элемента 2И;

ИС 1533ЛЛ1(74АLS32) − четыре логических элемента 2ИЛИ; ИС 1533ЛП5(74АLS86) − четыре двухвходовых логических элемента ИСКЛЮЧАЮЩЕЕ ИЛИ.