Цифровыеустройства. Технология idl
 Скачать 3.16 Mb.
|
Дизъюнктивная нормальная формаПреобразуем выражение (2.1) следующим образом: f(x1, x2 , x3 ) (x1 x2 x3)(x2 x1x3 ) x1x2 x1x1x3 x2 x3x2 x2 x3x1x3 x1x2 x1x3 x2 x3 . (2.2) 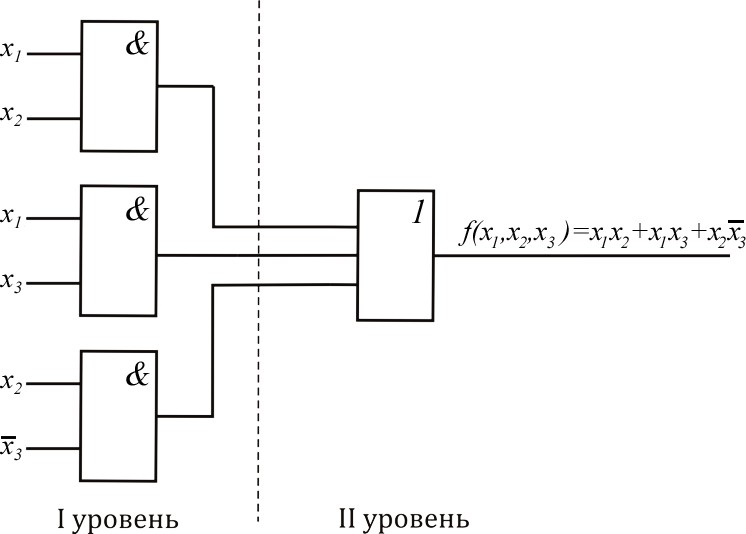 Представление ФАЛ в таком виде (2.2) известно как представление ФАЛ в дизъюнктивной нормальной форме. Итак, формы ФАЛ, представ- ляющие дизъюнкцию элементарных конъюнкций, называются дизъюнктив- ными нормальными формами (ДНФ). Под элементарной конъюнкцией по- нимается логическое произведение отдельных переменных в нормальном или инвертированном виде. Функция, представленная в ДНФ, может быть реали- зована с помощью И-ИЛИ конфигурации (рис. 2.3).Рис. 2.3. Реализация ФАЛ, представленной в ДНФ (И-ИЛИ конфигурация) Реализация ФАЛ (см. рис. 2.3) известна как двухуровневая реализация. Первый уровень состоит из И элементов, а второй уровень –из элемента ИЛИ.   Используя закон де Моргана, выражение (2.2) можно переписать сле- дующим образом: f(x1, x2 , x3 ) x1x2 x1x3 x2 x3 x1x2 x1x3 x2 x3 . (2.3) 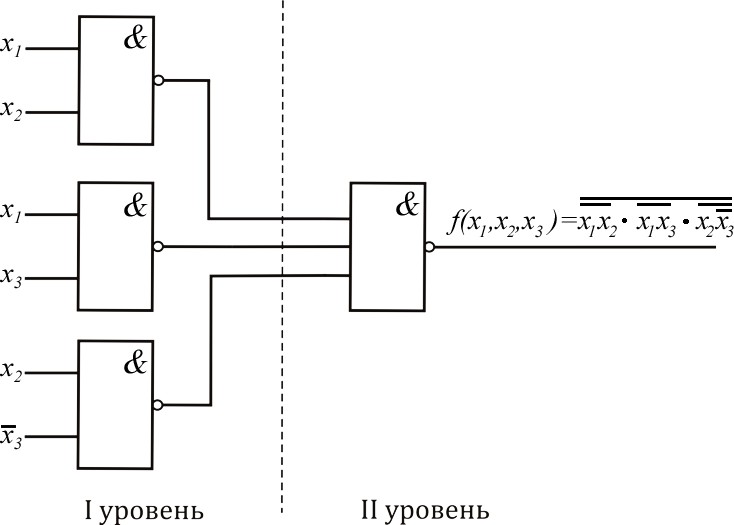 Теперь функция (2.3) может быть реализована с использованием толь- ко И-НЕ элементов (рис. 2.4).Рис. 2.4. Реализация ФАЛ, используя только И-НЕ элементы Вывод.Для того чтобы реализовать ФАЛ с помощью только элементов И-НЕ, необходимо представить ФАЛ в ДНФ, а затем использовать двойное инвертирование и закон де Моргана. Опять преобразуем исходную ФАЛ, используя распределительный за- кон для оператора И : f(x1, x2 , x3 ) x1 x2 x3 (x2 x1x3 ) (x1 x2 )(x1 x3 )(x2 x1)(x2 x3 ) (x1 x2 )(x1 x3 )(x2 x3 ) . (2.4) Представление ФАЛ в виде(2.4)известно как представление ФАЛ в конъюнктивной нормальной форме. Итак, формы ФАЛ, представляющие конъюнкцию элементарных дизъюнкций, называются конъюнктивными нор- мальными формами (КНФ). Под элементарной дизъюнкцией понимается ло- гическая сумма отдельных переменных в нормальном или инвертированном виде. Функция, представленная в КНФ, может быть реализована путем ис- пользования ИЛИ-И конфигурации (рис. 2.5). 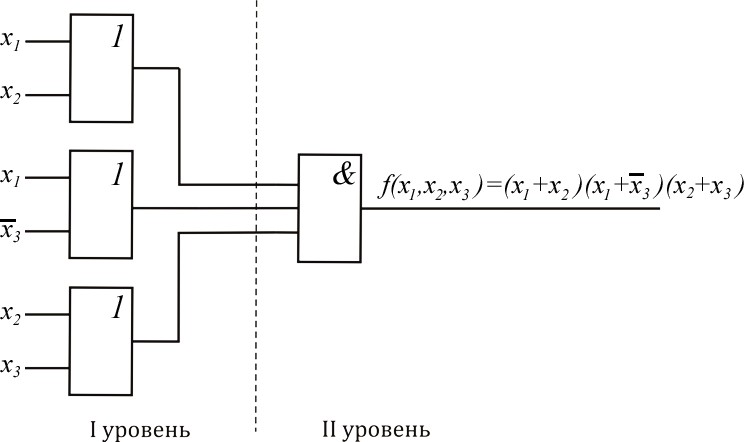 Рис. 2.5. Реализация ФАЛ, представленной в КНФ (ИЛИ-И конфигурация) Используя двойную инверсию и закон де Моргана, выражение (2.4) можно переписать следующим образом:   f(x1, x2 , x3 ) (x1 x2 )(x1 x3 )(x2 x3 ) x1 x2 x1 x3 x2 x3 . (2.5) 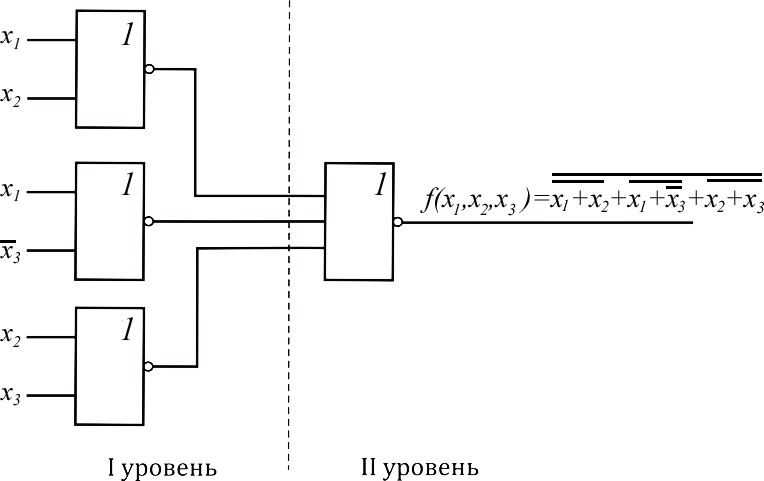 Теперь функция может быть реализована с использованием только ИЛИ-НЕ элементов(рис. 2.6).Рис. 2.6. Реализация ФАЛ, используя только ИЛИ-НЕ элементы Вывод. Для того чтобы реализовать ФАЛ с помощью только ИЛИ-НЕ элементов, необходимо представить ФАЛ в КНФ, а затем использовать двой- ное инвертирование и закон де Моргана. Теперь рассмотрим,как выражения(2.2)и (2.4)могут быть упрощены :  а)f(x,x,x) xx xx xx3 xx(x x3 ) xx xx3 1 2 3 1 2 1 3 2 1 2 3 1 3 2 xx xxx3 xx xx3 xx(x1) xx3 (x1) xx xx3 ; (2.6) 1 2 3 1 2 1 3 2 1 3 2 2 1 1 3 2 б)f(x, x, x) (x x)(x x3 )(x x) (x x xx3 )(x x3 ) 1 2 3 1 2 1 2 3 1 2 3 1 (x x) (x x x)(x x x3 )(x x3 )(x x) 2 3 1 2 3 1 2 1 2 3 (x x)(x x). (2.7) 1 3 2 3 Реализация выражений (2.6) и (2.7), используя только элементы И-НЕ и ИЛИ-НЕ, показана на рис. 2.7. 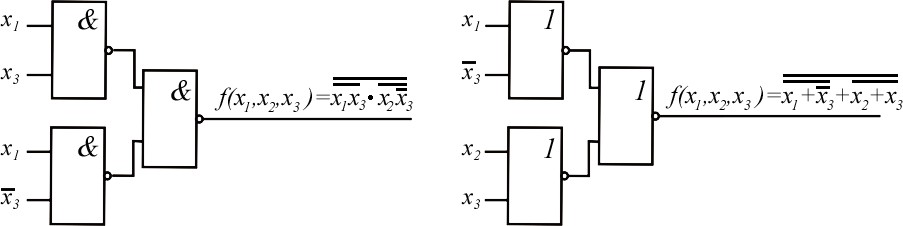 Рис. 2.7. Реализация функции после упрощения |