Цифровыеустройства. Технология idl
 Скачать 3.16 Mb. Скачать 3.16 Mb.
|
3.1.1 ПолусумматорПолусумматор может быть использован для сложения двух наименее значащих бит А0 и В0 двух чисел, где отсутствует входной перенос. Услов- ное обозначение полусумматора показано на рис. 3.1. 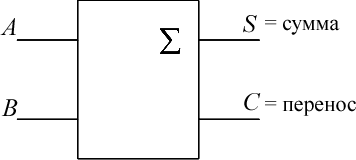 Рис. 3.1. Условное обозначение полусумматора Таблица 3.1
Из таблицы истинности полусумматора (табл. 3.1) можем получить ло- гические выражения для S и С. S ABAB A B; (3.1) ABС. (3.2) В соответствии с выражениями (3.1) и (3.2) полусумматор может быть легко реализован с помощью логических элементов ИСКЛЮЧАЮЩЕ ИЛИ и И(рис. 3.2). 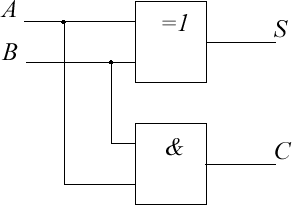 Рис. 3.2. Схема полусумматора Полный сумматорПолусумматор имеет только два входа и не имеет возможности сумми- ровать перенос из младшего разряда при многобитовом сложении. Для этих целей используется третий вход и схема осуществляет сложение An, Bnи С1, nгде An, Bn– это биты чисел A и B в разряде n, а С 1–nэто перенос при сложении из 1 разряда. Таблица 3.2
Логические выражения для S и C могут быть упрощены с помощью карт Карно (рис. 3.3). 1 BCBC 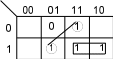 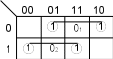 nnn1 nnn1AA nn n Рис. 3.3. Упрощение выражений для Sи C n полного сумматора Логическое выражение для S может быть упрощено в базисе функций ИСКЛЮЧАЮЩЕЕ ИЛИ. Sn ( AnBnCn1 AnBnCn1) ( AnBnCn1 AnBnCn1) An(Bn Cn1) An(Bn Cn1) An Bn Cn1 . (3.3) ФАЛ для Спможет быть покрыта с помощью обычного логического соседства, а также диагонального соседства (рис. 3.3). Сn ( AnBnСn 1 AnBnС1) ( AnBnС 1 AnBnС1) Сn1(An Bn) AnBn. (3.4) В соответствии с выражениями (3.3) и (3.4) на рис. 3.4 показана схема полного сумматора. 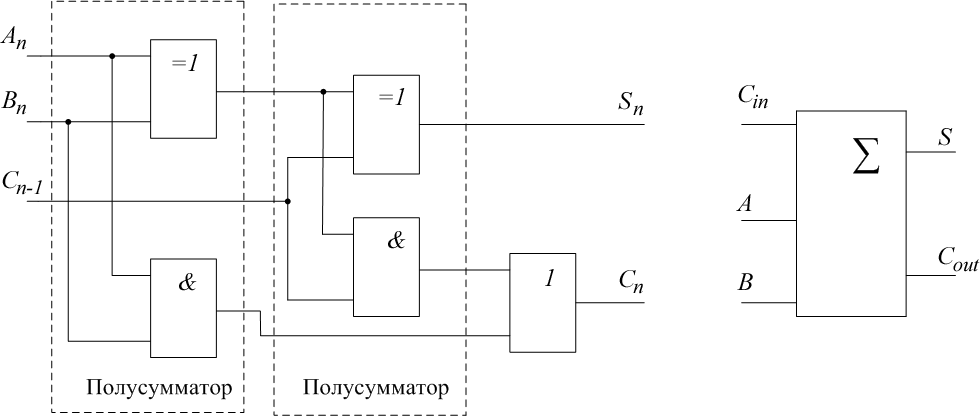 а б Рис. 3.4. Полный сумматор: а –логическая схема; б – условное обозначение | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
