Цифровыеустройства. Технология idl
 Скачать 3.16 Mb. Скачать 3.16 Mb.
|
Параллельный сумматорДля сложения четырехразрядных двоичных чисел четыре полных сум- матора могут быть соединены, как показано на рис. 3.5, для получения четы- рехразрядного параллельного сумматора. Два четырехразрядных двоичных числа подаются на входы Аи Вчетырех полных сумматоров. А0 ,В0 – это, конечно, наименее значимые биты. Выход переноса Сout каждого сумматора соединен непосредственно с входом переноса Сin следующего более значи- мого полного сумматора. Выход Сout наиболее значимого разряда является переносом всей схемы.Биты переноса передаются через схему от разряда к разряду, и индивидуальная сумма будет правильной, когда перенос из пре- дыдущего разряда появится в данном разряде. Это означает, что выходная или полная сумма появится, когда все биты переноса пройдут через схему. Поэтому такую схему (рис. 3.5, а) более точно называют псевдопараллель- ным сумматором. В интегральном исполнении выпускается четырехразрядный парал- лельный сумматор 1533ИМ3(74АLS83) (рис. 3.5, б). 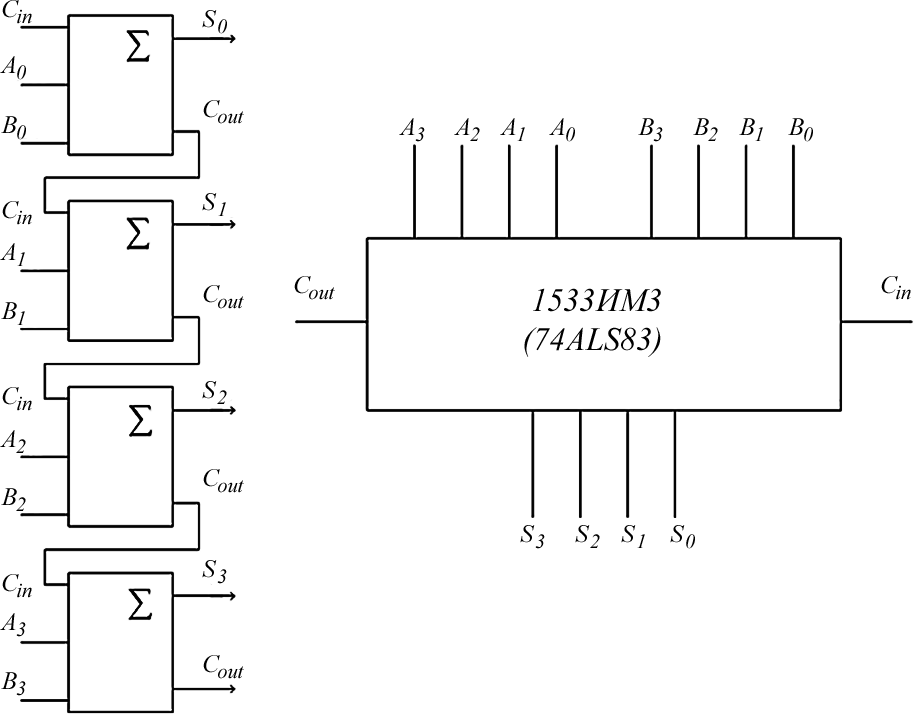 а б а бРис. 3.5. Параллельный сумматор ВычитателиПолувычитатель Логическая схема, которая осуществляет вычитание B(вычитаемое) из A(уменьшаемое), где Aи B– это однобитовые числа, называется полувычита- телем. Процесс вычитания может быть представлен с помощью таблицы ис- тинности (табл. 3.3). Таблица 3.3
Здесь Аи В– это входы, а выходы D– разность и С– заем. Из таблицы истинности (см. табл. 3.3)
В соответствии с выражениями (3.5) и (3.6) логическая схема полувычи- тателя показана на рис. 3.6. 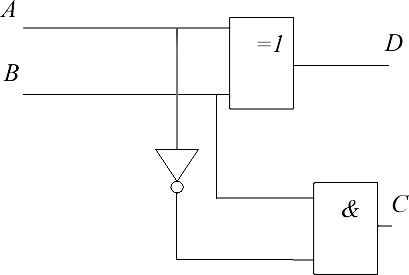 Рис. 3.6. Логическая схема полувычитателя Полныйвычитатель Для выполнения многобитового вычитания необходим полный вычита- тель, где заем из предыдущего разряда присутствует. Таким образом, полный вычитатель имеет три входа: Ап(уменьшаемое), Вп(вычитаемое) и Сп 1 (за- ем от предыдущего разряда) и два выхода Dп(разность) и Сп(заем). Таблица 3.4
Таблица истинности (табл. 3.4) и карта Карно для выхода Dпточно та- кие же, как и для Sпв полном сумматоре, поэтому АD В С1. (3.7) Карта Карно для Сп показана на рис. 3.7. 1 BC 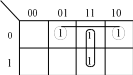 n nA  C A(B C) BC C A(B C) BCnn n1 nn1 Рис. 3.7. Упрощение для Сс помощью карты Карно Существует три варианта упрощения выражения для заема С. Два из них дают схему полного сумматора, состоящего из двух полувычитателей и схемы ИЛИ. Однако наиболее интересным представляется третий вариант (см. рис. 3.7): n ( n nn1 nnn1) ( nnn1 nnAAСAСBnСBBB1) n( n n1) nСAnBС1 .B (3.8) Логическая схема полного вычитателя для этого варианта показана на рис. 3.8. 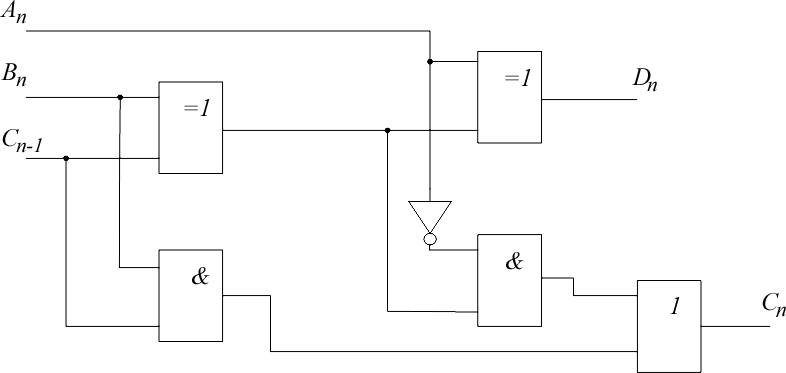 Рис. 3.8. Полный вычитатель Рис. 3.8. Полный вычитательПолный вычитатель (см. рис. 3.8) по сравнению с обычной схемой не состоит из двух полувычитателей, а содержит на один логический элемент (инвертор) меньше и время распространения сигнала через схемы на один элемент меньше, т. е. схема полного вычитателя (см. рис. 3.8) более быстро- действующая по сравнению с обычной схемой полного вычитателя. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
