Цифровыеустройства. Технология idl

• Название: Цифровыеустройства. Технология idl
• Дата: 15.02.2022
• Размер: 3.16 Mb.
• Имя файла: Budko_CU.docx
• Тип: Документы; #362193
• страница: 21 из 46

Реализация функции m+1 переменных на мультиплексорах с m адресными входами

Рассмотрим это на примере.

Пример 5.2. Реализовать ФАЛ, заданную таблицей истинности

(табл. 5.2).

Решение. ФАЛ четырех переменных может быть реализована, исполь-

зуя мультиплексор размерностью 8:1 (рис. 5.4). Переменные ФАЛ

^x1,

^x2 , ^x₃

подсоединим к адресным входам

^S2 ,

^S1 ,

^S0 соответственно. Переменную, не

подсоединенную к адресным входам, называют «выделенной». Без выделен-

ной переменной наборы переменных

^x1,

^x2 ,

^x₃ образуют пары. В таблице

истинности (см. табл. 5.2) эти пары выделены пунктирными линиями. Теперь рассмотрим соотношения между выделенной переменной
^x4 и

выходом для каждой пары. При этом возможны четыре варианта, когда вы-

ход ^Yне зависит от переменной ^x4

и равен 0 или 1 и когда выход ^Yзависит от Таблица 5.2

Входы Выход
x1	x2	x3	x4	Y
0	0	0	0	1
0	0	0	1	1
0	0	1	0	0
0	0	1	1	1
0	1	0	0	0
0	1	0	1	1
0	1	1	0	1
0	1	1	1	1
1	0	0	0	0
1	0	0	1	0
1	0	1	0	1
1	0	1	1	0
1	1	0	0	0
1	1	0	1	1
1	1	1	0	1
1	1	1	1	0

1
x₄ x₄ 1

0



x

4
x

4




^x4

переменной

^x4 и равен

^x4 или

^x4 ^{, как отмечено справа от таблицы истинно-}

сти. Исходя из этого на информационные входы мультиплексора и подается

лог. 0, лог. 1,

^x4 или

^x4 ^{, как показано на рис. 5.4.}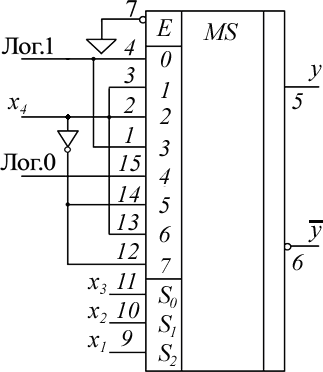

Рис. 5.4. Реализация ФАЛ, пример 5.2, с использованием мультиплексора КР1533КП7(74ALS151)
Для синтеза ФАЛ можно использовать карты Карно (рис. 5.5). Парные наборы на ней расположены рядом, т. е. являются соседними. Объединим эти

наборы и пометим числом, соответствующим наборам переменных

^x1,

^x2 ,

^x₃ . Можно заметить, что парные наборы легко выделяются проведением раз-

делительных линий по переменным

^x1,

^x2 ,

^x₃ (рис. 5.5, б). После объедине-

ния парных наборов получается карта Карно для трех переменных.



а б в Рис. 5.5. Синтез ФАЛ с помощью карт Карно

Зададим теперь ФАЛ с помощью карты Карно (рис. 5.5,в).Сопостав-

ляя рис. 5.5, б и рис. 5.5, в, можно заметить, что в клетке с номером 0 ^Y1 и,

следовательно,

₀ ^I1. В клетке с номером 1

^{Y x4} , что дает

I₁

^x4 . Про-

должая рассмотрение дальше, получим итоговый результат:

I₀ I

₃ ^{ 1},

  I₁ I₂ I₆

^x4 , <sup>I4

0</sup> ,

I₅ I₇

^x4 .

До сих пор мы различали парные наборы по переменной

^x4 , которая

затем подавалась на информационные входы. Однако в качестве «выделен- ной» может быть взята любая переменная. Более того, для технической реа- лизации не безразлично,какую переменную следует выделять. Это связано с тем, что выбор выделенной переменной определяет количество информаци- онных входов, на которые подаются константы 0, 1. Такие информационные входы не нагружают предыдущие цепи, поэтому их желательно иметь как можно больше. Очевидно, что для достижения этого в качестве выделенной следует использовать переменную, от которой ФАЛ зависит меньше всего.

Последнее можно установить по минимальной дизъюнктивной форме, под- считав количество вхождений переменной в эту форму как с инверсией, так и без нее.