Цифровыеустройства. Технология idl
 Скачать 3.16 Mb. Скачать 3.16 Mb.
|
Исследование вычитателейПолувычитатель Используя логические элементы, собрать схему полувычитателя (см. рис. 3.6). Изменяя состояния входов А и В, исследовать работу полувычитате- ля, получить таблицу истинности полувычитателя (см. табл. 3.3). Полныйвычитатель Используя логические элементы, собрать схему полного вычитателя (см. рис. 3.8). Изменяя состояния входов А, В, С 1, исследовать работу полного вычитателя, получить таблицу истинности полного вычитателя (см. табл. 3.4). Исследование суммирования/вычитания в дополнительном коде1. Собрать схему сумматора/вычитателя (см. рис. 3.9). 2.Исследовать работу сумматора/вычитателя,используя несколько примеров. Числа Аи Впредставляются в дополнительном коде. 3. Объяснить результаты экспериментов. СОДЕРЖАНИЕ ОТЧЕТА Цель работы. Схемы, исследуемые в работе. Таблицы, отражающие результаты исследований. Выводы по результатам исследований. КОНТРОЛЬНЫЕ ВОПРОСЫ Какие комбинационные схемы называются полу/полным суммато- ром (вычитателем)? Нарисуйте схему полу/полного сумматора (вычитателя). Напишите таблицу истинности полу/полного сумматора (вычитателя). Примеры суммирования/вычитания в дополнительном коде. Лабораторная работа №4 ИССЛЕДОВАНИЕ ПРЕОБРАЗОВАТЕЛЕЙ КОДОВЦельработы: Синтез преобразователей двоичных кодов. Исследование функционирования преобразователей двоичных кодов. ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ Для представления информации в цифровых устройствах используются двоичные коды. И хотя любой код, используемый для представления инфор- мации, имеет двоичную форму, однако правильная интерпретация этих кодов возможна, только если этот код известен. Наиболее часто используемые дво- ичные коды представлены в табл. 4.1. Таблица 4.1
Прямойдвоичныйкод Используется для представления чисел в двоичной системе счисления. В табл. 4.1 прямой двоичный код представляет числа от 0 до 15. Двоично-десятичный8-4-2-1код(ВСD-код) Используется для представления десятичных цифр. Числа 8, 4, 2 и 1 яв- ляются весами разрядов. Запись десятичной цифры в коде 8-4-2-1 совпадает с записью двоичных чисел от0до 9,а -разрядное десятичное число пред- ставляется с помощью тетрад, каждая из которых состоит из четырех двоич- ных разрядов (например 39510 0011 1001 0101). Двоично-десятичныйкодсизбытком3(Excess-3код) Excess-3 код (также используемый для представления десятичных цифр) образуется от соответствующих представлений цифр в ВСD-коде пу- тем прибавления двоичного числа 0011. Код с избытком 3 является самодо- полняющим кодом. Правила преобразования прямого кода с избытком 3 в дополнительный с избытком 3 и правила обратного преобразования такие же, как и для двоичного дополнительного кода. Поэтому код с избытком 3 часто удобнее использовать для выполнения арифметических операций. При этом для сложения четырехразрядных кодов можно использовать четырехразряд- ные двоичные сумматоры. Код Грея В коде Грея десятичные числа представлены в двоичном виде таким образом, что представление каждого числа отличается от предыдущего как и от последующего только в одном бите (разряде). Код Грея является зеркальным и может быть построен следующим об- разом. Одноразрядный код Грея состоит из кодовых слов, 0 и 1, которые представляют десятичные числа 0 и 1. В -разрядном ( п 2) коде Грея первые 2п1 кодовых слова повто- ряют ( 1)-разрядный код Грея с приписанным 0 в крайнем левом разряде. Последние 2п1 кодовые слова представляют кодовые слова( п 1)- разрядного кода Грея, записанными в обратном порядке (как будто между первыми 2п и последними 2п1 кодовыми словами размещено зеркало) и дописанной 1 в крайнем левом разряде. Например, определим одноразрядный, двухразрядный и трехразрядный код Грея. Для одноразрядного кода Грея
Для двухразрядного кода Грея  Для трехразрядного кода Грея 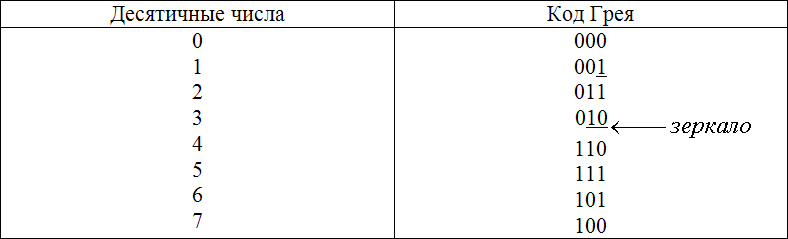 Очень часто в цифровых системах возникает задача преобразования двоичной информации, представленной в одном двоичном коде, в другой код. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
