Газидинамический профиль камеры. ЖРД Курсовой. Д. А. Жуйков (подпись, дата) (инициалы, фамилия)
 Скачать 0.97 Mb. Скачать 0.97 Mb.
|
|
Федеральное государственное бюджетное образовательное учреждение высшего образования «Сибирский государственный университет науки и технологий имени академика М.Ф. Решетнева» Кафедра Двигатели летательных аппаратов Дисциплина Теория и проектирование турбонасосных агрегатов Группа Д15-01 ЗАДАНИЕ НА КУРСОВУЮ РАБОТУ 1. Тема проекта Расчет и проектирование турбонасосного агрегата Дата выдачи «____» ______________ 2018 г. Срок сдачи проекта «____» ______________ 2019 г. Руководитель проекта _________ Д. А. Жуйков (подпись, дата) (инициалы, фамилия) Студент _________ А. С. Погорелов (подпись, дата) (инициалы, фамилия) Оглавление Введение 3 ЗАДАНИЕ 4 1. Определение удельной формулы топлива 5 1.1 Молекулярная масса вещества 5 1.2 Удельная формула вещества 5 1.3 Удельная формула окислителя 5 1.4 Массовое стехеометрическое соотношение компонентов 5 1.5 Массовое действительное соотношение компонентов 6 1.6 Расчёт удельной формулы топлива 7 2. Определение полной энтальпии 7 3. Параметры в камере двигателя 7 3.1 Расчёт удельного импульса 8 3.2 Основные параметры в камере двигателя 9 4. Построение контура камеры двигателя 10 5. Построение графиков 11 6. Дроссельная и высотная характеристики 16 Расчет охлаждения 18 7. Определение лучистых тепловых потоков 18 8. Определение теплопередачи от продуктов сгорания к охлаждающей жидкости 20 9. Расчет α2 22 10. Расчет охлаждения 23 ВведениеМетодические указания закрепляют курс лекций по теории жидкостных ракетных двигателей. Цель данной курсовой работы заключается в том, чтобы рассчитать основные параметры камеры двигателя (КД), включая расчет тракта охлаждения. Материал дает представление о процессах горения и истечения, методах их количественного описания и позволяет выполнить соответствующие расчеты. Рассматриваются свойства топлива и продуктов сгорания (ПС); система уравнений для расчета гомогенного и гетерогенного состава смеси реагирующих газов (из четырех химических элементов H, C, N, O) при заданном давлении и метод решения этой системы; приводится порядок расчета температуры ПС в камере сгорания (температуры горения), равновесного и замороженного истечения, идеального и действительного удельного импульса, расходного комплекса, основных размеров и контура камеры двигателя, параметры охлаждающего тракта, расчет лучистого и конвективного теплообмена в КД. Основные зависимости исследования процессов течения газов выводятся при анализе уравнения неразрывности и двух уравнений первого закона термодинамики, написанных для зафиксированных и подвижных осей координат. Расчет истечения начинают с определения области течения, которая может быть дозвуковой, звуковой, сверхзвуковой. Ее находят сравнением перепада давления с критическим перепадом , являющимся функцией свойств продуктов сгорания. Однако путем такого сравнения можно определить лишь возможность получения той ли иной скорости. Чтобы эта возможность стала действительностью, необходима соответствующая форма сопла. Канал, в котором достижима сверхзвуковая скорость, называется соплом Лаваля (по имени шведского инженера , предложившего это сопло для получения сверхзвуковой скорости в струе пара, работающей в турбине). Сопло Лаваля состоит из сужающейся и расширяющийся частей. В сужающейся части скорость увеличивается от начального значения (если истечение происходит из большого сосуда, w=0) до скорости, равной местной скорости звука; в расширяющейся части наблюдается дальнейшее увеличение скорости потока. Для уменьшения потерь энергии расширяющаяся часть соединяется ссужающейся плавным переходом - горловиной. Это минимальное сечение, в котором достигается скорость движения потока, равная скорости звука, называется критическим сечением, а параметры газа - критическими. Для курсовой работы задают компоненты топлива в жидком состоянии, давление в камере сгорания Pк, давление на срезе сопла Pа, наружное Pн и тяга P. Для выполнения данного курсового проекта используется программа GRD55.exe, которая позволяет рассчитать параметры продуктов сгорания в КС и на срезе сопла, а так же удельный импульс и расходный комплекс, так же для построения КД используется пакет «Компас 3D», для расчета охлаждения используются табличный процессор «Google Sheets» и различные методические пособия и научная литература. ЗАДАНИЕПровести термодинамический расчет двигателя со следующими исходными данными: Окислитель 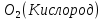 Горючее 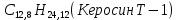 Давление в камере =24,5 МПа Давление на срезе =0,078 МПа Давление наружное =0.050 МПа Тяга P=1850 кН Количество камер 1 Необходимо выполнить следующие расчеты: -рассчитать стехиометрическое соотношение компонентов, удельную формулу и энтальпию топлива; -для  -для  -для 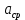 состав ПС в камере сгорания и на срезе состав ПС в камере сгорания и на срезе 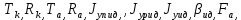 потери в потери в 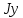 на замороженность в процентах, потери на охлаждение на замороженность в процентах, потери на охлаждение 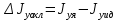 в процентах. в процентах.- параметры камеры двигателя (КД): размеры и контур КД. Основные результаты расчетов, а именно: 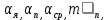 , удельную формулу топлива , удельную формулу топлива 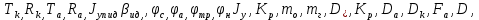 представить в пояснительной записке в виде таблицы после начальных данных. представить в пояснительной записке в виде таблицы после начальных данных.Построить графические зависимости: - состав ПС в КС от  (в масштабе); (в масштабе);- 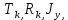 от от 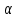 с нахождением с нахождением 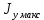 ; ;- состав ПС по длине КД (в масштабе и с контуром КД); -T, R, 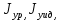 по длине КД (в масштабе и с контуром КД); по длине КД (в масштабе и с контуром КД);Часть 1. Термодинамический расчет жидкостного ракетного двигателя 1. Определение удельной формулы топливаЗапишем удельную формулу каждого вещества Горючее: Керосин Т-1 - химическая формула C12H24 Окислитель: Кислород - химическая формула O2 1.1 Молекулярная масса веществаДля горючего: 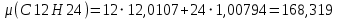 Для окислителя 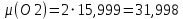 1.2 Удельная формула веществаДля горючего C12H24 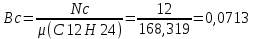 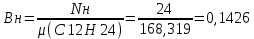 Получаем удельную формулу горючего Керосин Т-1: C0,0713H0,1426 1.3 Удельная формула окислителя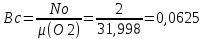 Получаем удельную формулу окислителя Кислород: О0,0625 1.4 Массовое стехеометрическое соотношение компонентов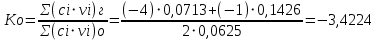
1.5 Массовое действительное соотношение компонентов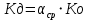 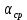 - коэффициент избытка окислителя - коэффициент избытка окислителяРк=24,50 МПа; - Давление в КС Ра=0,078МПа; - Давление на срезе Pн=0,050 МПа; - Атмосферное давление Используя компьютерное приложение, рассчитываем удельный импульс
Уточним выборы коэффициента до 2-го знака в пределе [0,8;0,9]
При значении 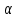 =0,86, Iy=3370, приложение выдаёт прирост 0% по сравнению с =0,86, Iy=3370, приложение выдаёт прирост 0% по сравнению с 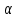 =0,85 и =0,85 и 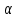 =0,87, поэтому принимаем, что =0,87, поэтому принимаем, что 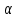 =0,87; Iy=3370 =0,87; Iy=3370Определяем 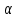 в пристеночном слое, приняв в пристеночном слое, приняв 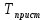 =2000К, получаем =2000К, получаем 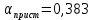 ; R=508,3 ; R=508,3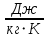 ; ;  Определяем 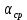 , приняв , приняв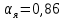 ; ; 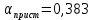 ; ; 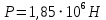 Получаем, что 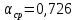 Действительный коэффициент соотношения компонентов 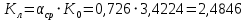 1.6 Расчёт удельной формулы топлива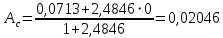 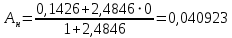 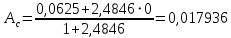 Удельная формула топлива 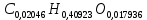 2. Определение полной энтальпии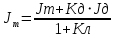 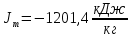 ; ; 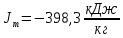 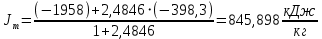 3. Параметры в камере двигателяДействительный удельный импульс 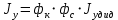 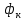 принимаем принимаем 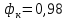 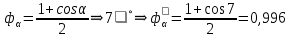 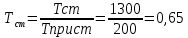 Находим угол раскрытия сопла в критическом сечении 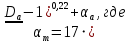 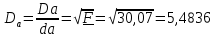 . .( 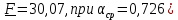 , тогда , тогда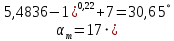 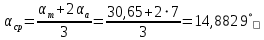 Значение 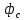 принимаем принимаем 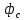 =0,98, проверим его =0,98, проверим его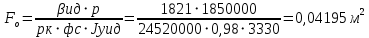 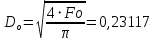 м м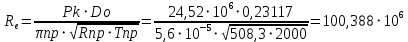 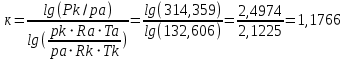 где гдеTa=1682 К; Tk=3801 К Ra=338,5; Rk=355,1 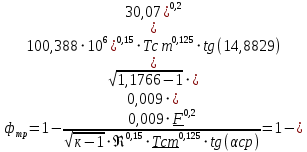 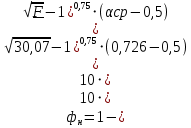 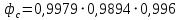 =0,9833 =0,9833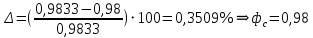 верно верно3.1 Расчёт удельного импульсаДля расчета Iуд примем Фс=0,983, полученное расчетным путем, тогда 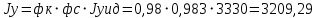 м/c м/cНайдем потери удельного импульса при изменении режима истечения с равновесного на замороженный Iуз=3170 м/с 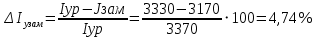 Находим потери на охлаждение 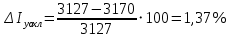 3.2 Основные параметры в камере двигателяРасход топлива 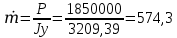 кг/с кг/сРасход горючего 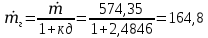 кг/с кг/сРасход окислителя 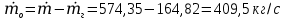 Площадь критического сечения 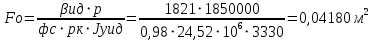 Диаметр критического сечения 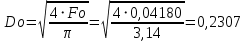 м м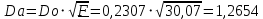 м мОбъем камеры сгорания Vкс=Fo  Lпр, где Lпр, где 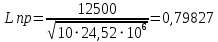 , тогда , тогда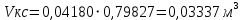 Площадь поперечного сечения КС 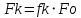 , где , где 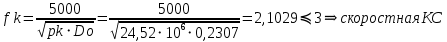 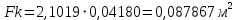 Диаметр КС 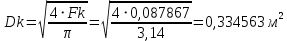 Расходный комплекс 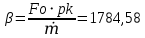 Тяговый комплекс 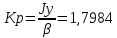 4. Построение контура камеры двигателя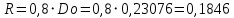 м м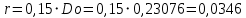 м м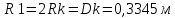 Вычисляем длину цилиндрической части КС 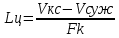 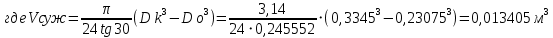 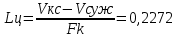 м мДлина сверхзвуковой части сопла 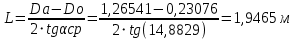 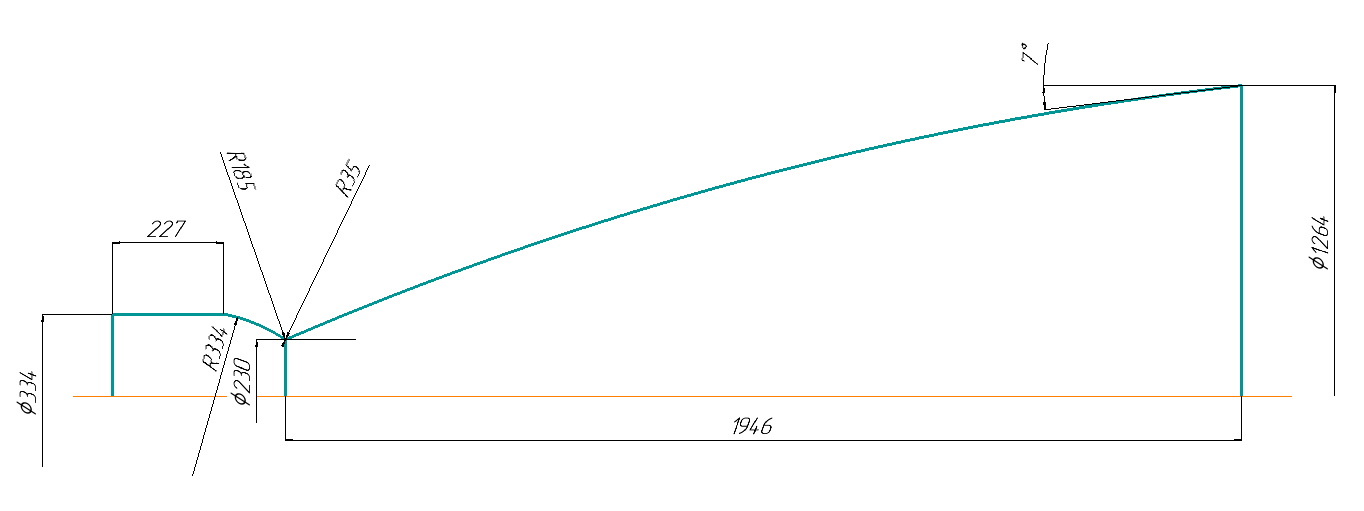 5. Построение графиков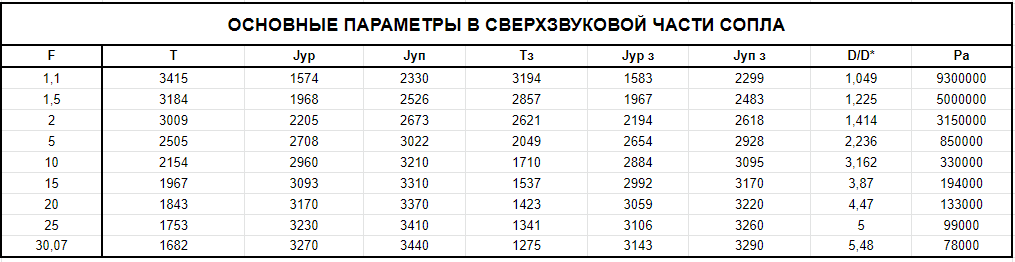 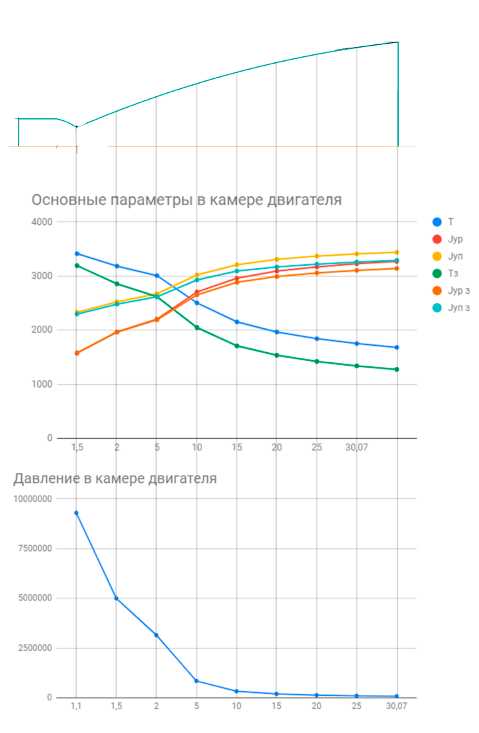 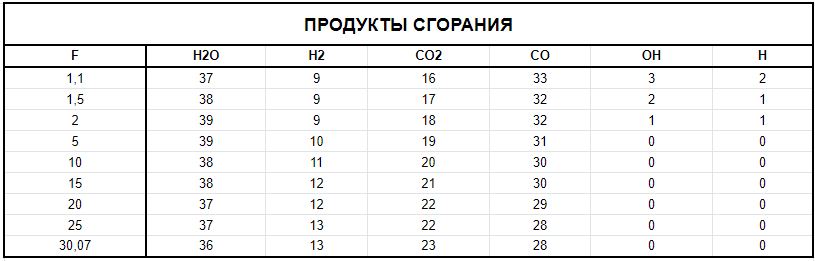 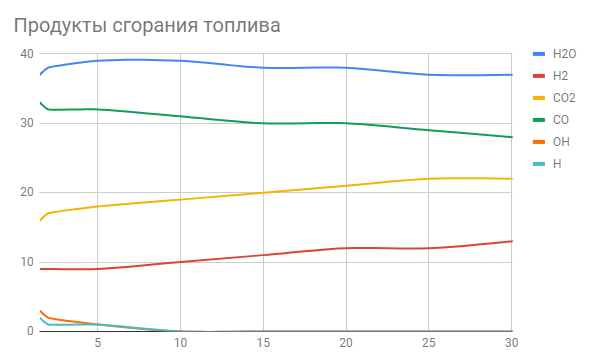 6. Дроссельная и высотная характеристики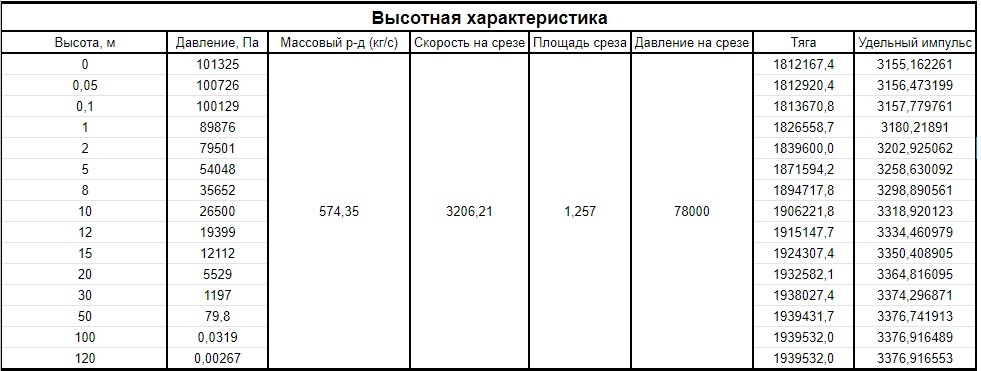 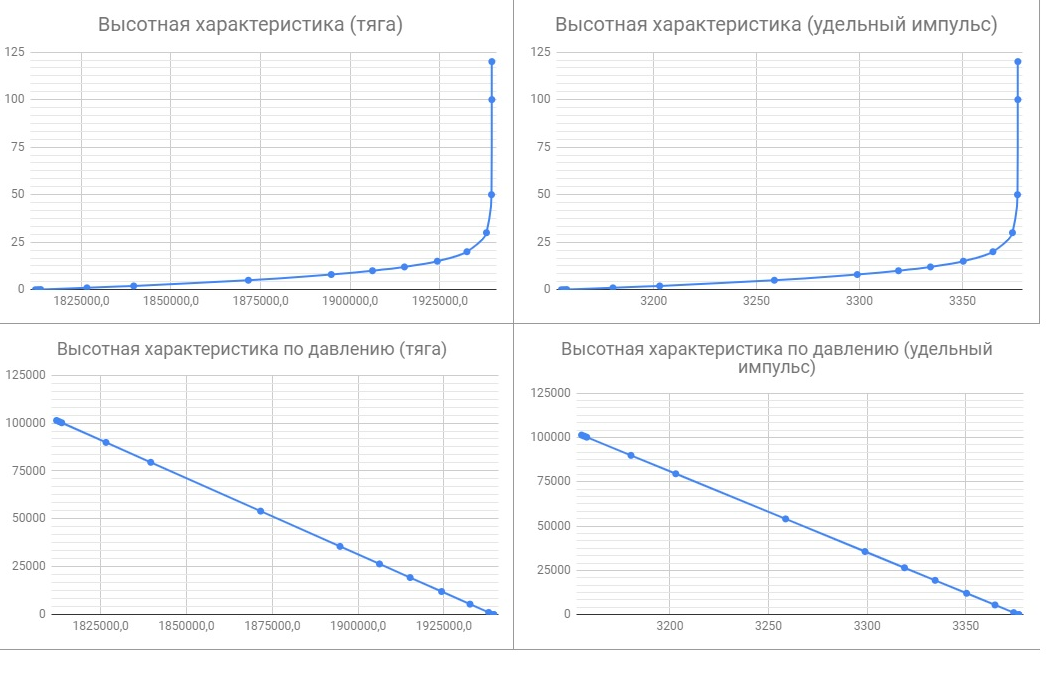 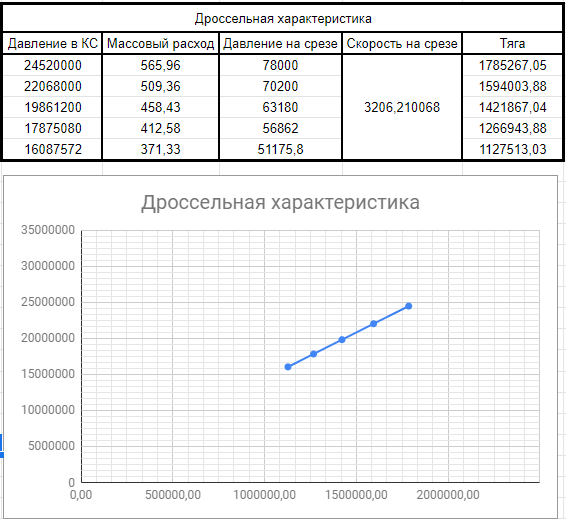 Расчет охлаждения7. Определение лучистых тепловых потоковВ камере двигателя происходит излучение продуктов сгорания. Излучательная и поглощательная способность газов, входящих в состав продуктов сгорания, различна. Наибольшей излучательной и поглощательной способностью обладают многоатомные газы, в первую очередь, пары Н2О и СО2. Для определения лучистых тепловых потоков воспользуемся эмпирическими формулами: 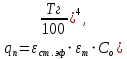 где Со=5,67 Вт/(м2К4) – коэффициент излучения абсолютно черного тела, Тг – температура продуктов сгорания (К), а значения εст.эф и εг определяются: εг=εН2О+εСО2- εН2ОεСО2 εН2О=1-(1- εоН2О)n εоН2О определяем по графикам, полученным путем экстраполяции данных Хоттеля и Эгберта. εоН2О=0,9 n=1.3 εН2О=1-(1-0.9)1.3=0.95 εСО2=0.5, тогда εг=0,95+0,5+0,95*0,5=0,975 εст.эф= εст(1+(1- εст)(1- εг))=0,7(1+(1-0,7)(1-0,975))=0,705 для стали примем εст=0,7 можем найти лучистые тепловые потоки: 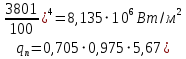 Для определения qл в различных областях камеры с достаточной степенью точности, примем: - в камере сгорания на 60мм от смесительной головки q=0,8 qл=6,508*106 ВТ/м2 и возрастает до qл - в дозвуковой части сопла постоянный до диаметра D=1.2Dкр. -в закритической части сопла до диаметра D=1.5Dкр, q=0,1 qл=8,135*105 ВТ/м2 -в сечении, где D=2.5Dкр , q=0,02 qл=1,62*105 ВТ/м2 и остается постоянным до среза сопла. 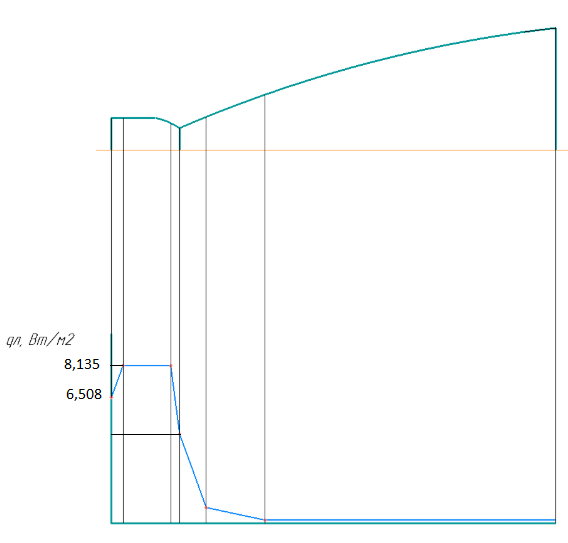 Рис. 6. График изменения лучистых тепловых потоков по длине камеры 8. Определение теплопередачи от продуктов сгорания к охлаждающей жидкостиДля определения теплопередачи от продуктов сгорания к охлаждающей жидкости рассмотрим отдельно теплоотдачу от продуктов сгорания к огневой стенке q1, теплопередачу внутри стенки q2, теплоотдачу от стенки к охлаждающей жидкости q3, а в качестве проверки будем использовать формулу теплопередачи q: q1=α1(Т1-Т2) q2= (Т2-Т3) q3=α2(Т3-Т4) q=k(Т1-Т4) k= 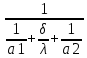 , где , гдеα1 - коэкоэффициент теплоотдачи от стенки к жидкости, α2 - - коэкоэффициент теплоотдачи от стенки к охлаждающей жидкости, Т1 – температура продуктов сгорания в пристеночном слое, Т2 – температура стенки со стороны продуктов сгорания Т3 – температура стенки со стороны жидкости, Т4 – температура жидкости, λ – коэффициент теплопроводности стенки, δ – толщина стенки, k – коэффициент теплопередачи. Для расчета охлаждения необходимо определить неизвестные величины α1, Т2, α2, Т3. Определять их будем методом последовательных приближений, т.к. все тепловые потоки q1, q2, q3, q должны быть между собой равны. На несовершенство расчета примем допустимую погрешность Δ, которая не должна превышать 5%. Также разобьем камеру на конечное количество областей: 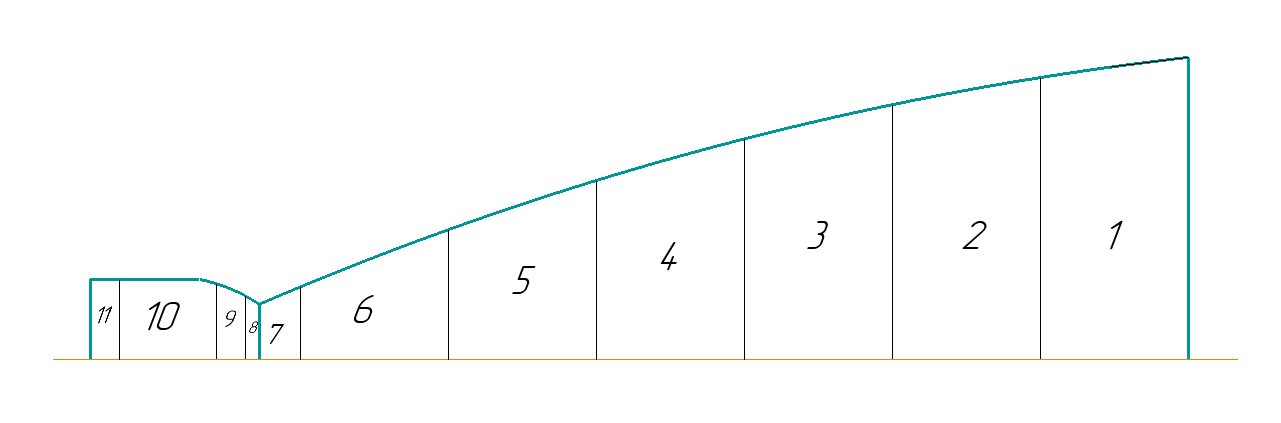 Проведем расчет для области 1: Коэффициент теплоотдачи α1: 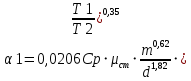 , где , гдеСр=3490 – теплоемкость продуктов сгорания, μст=99*10-6 – вязкость продуктов сгорания, m=574,36 кг/с – массовый расход, d=1,264 м – диаметр области (примем начальный). Для определения α2 необходимо учесть влияние ребер в охлаждающем тракте: α2=ηр*αж, где ηр – коэффициент оребрения, αж – коэффициент теплоотдачи от стенки к охлаждающей жидкости без учета ребер. Перед нахождением коэффициента оребрения зададимся геометрическими параметрами каналов в рубашке охлаждения: Ширина каналов а=4,5 мм, толщина ребер δр=1,75 мм, толщина стенки δст=1,5 мм, высота каналов hохл=4 мм. Так как при движении жидкости вдоль охлаждающего тракта диаметры рассчитываемых областей будут непостоянны, толщину ребер δр будем принимать как среднюю по длине области. В случае сужения ребер до толщины порядка 1 мм будем делать проточку с изменением числа каналов. В области 1 количество каналов n=600. 9. Расчет α2Перед расчетом в качестве охлаждающей жидкости примем керосин, т.к. его использование в качестве охладителя обусловлено высококипящими свойствами и простотой использования. Начальная температура керосина, попадающего в охлаждающий тракт Т4=293 К, а максимальную примем Т4max=623 K, что обусловлено высоким давлением. Суммарная площадь каналов охлаждающего тракта: f=а*hохл*n=0,011 м2 Эквивалентный диаметр тракта: 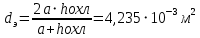 Коэффициент теплоотдачи от стенки к охлаждающей жидкости без учета ребер: 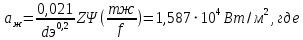 mж=100 кг/с – массовый расход охлаждающей жидкости через рубашку охлаждения, а комплекс Zψ=1,7*102 и установлен исходя из термодинамических графиков для керосина. Коэффициент оребрения: 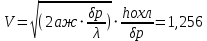 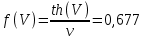 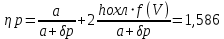 Коэффициент теплоотдачи от оребренной стенки к охлаждающей жидкости: α2= ηр* αж=2.517*104 Вт/м2 Температура Т1=2000 К и остается постоянной по всей длине камеры (температура пристеночного слоя). В качестве сравнительной величины примем тепловой поток q. 10. Расчет охлажденияНеизвестные температуры будем определять методом последовательных приближений. Примем Т2=488 К, Т3=455 К, таким образом конвективные тепловые потоки:   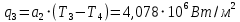 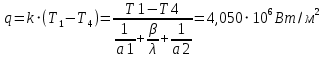  ; ;  ; ; 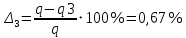 ; ;Величины расхождения не превышают ранее заданного предела Δ=5%, соответственно определенные тепловые потоки и температуры можно считать верными Количество тепла, переданного в стенку расчетной области равно:  , где , где  Диаметры d1 и d2 – диаметры начала и конца расчетной области соответственно, а l – ее длина. Определим, на сколько нагрелась жидкость при прохождении области:  Температура жидкости на выходе из области 1: 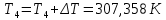 Расчет области 1 можем считать завершенным, а все данные по остальным вычислим с помощью табличного процессора и занесем в таблицу. 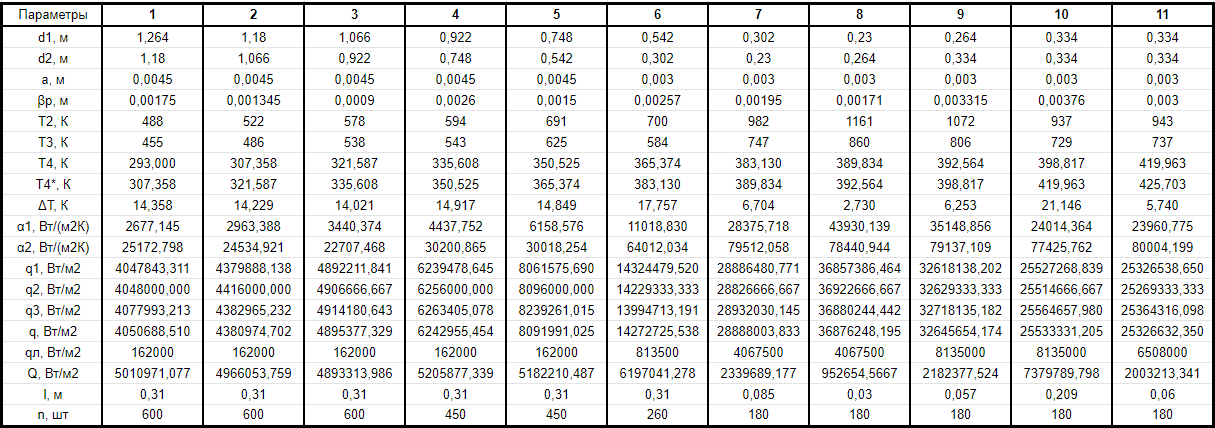 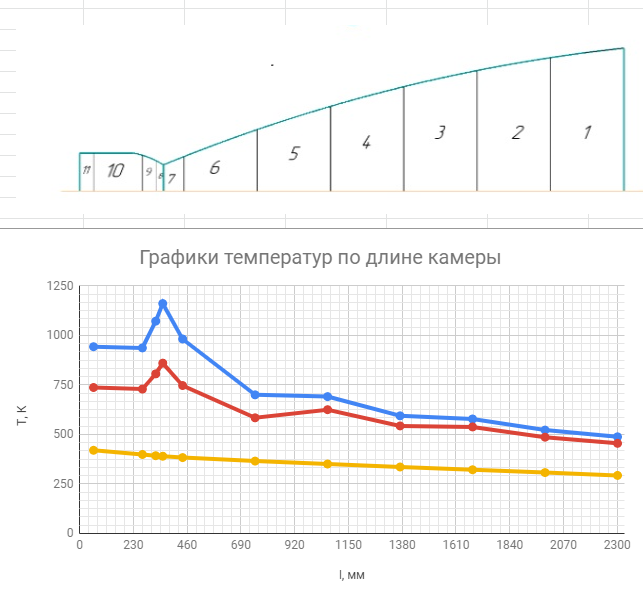 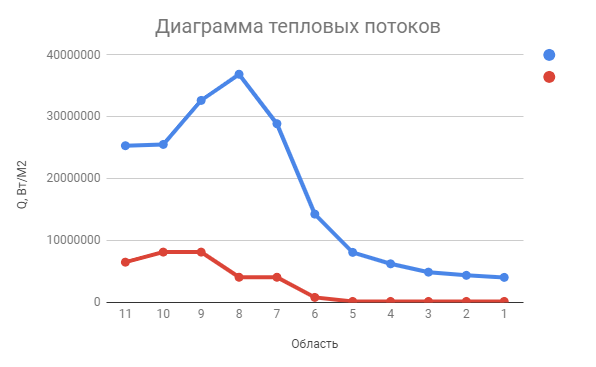 Так как температуры Т2 и Т3 не выходят за пределы допустимых, можем считать расчет охлаждения успешным Красноярск 2019г |
