Учебник по дискретной математики. Д. Ушинского Дискретная математика
 Скачать 2.66 Mb.
|
Бином Ньютона. Полиномиальная формула.
Рекуррентные соотношения.
a) аn+2-7an+1+12an=0; b) аn+2+3an+1-10an=0; c) аn+2+9an=0 ; d) аn+2+4an+1+4an=0.
Введение в теорию графов Среди дисциплин и методов дискретной математики теория графов и особенно алгоритмы на графах находят наиболее широкое применение в программировании. Дело в том, что теория графов дает очень удобный язык для описания программных моделей. Особенно важно наличие наглядной графической интерпретации понятия графа. Картинки позволяют сразу «усмотреть» суть дела на интуитивном уровне, дополняя и украшая утомительные рациональные текстовые доказательства и сложные формулы. Начало теории графов относят к 1736 г., когда Л. Эйлер решил задачу о Кениксбергских мостах. Около 100 лет это был единственный результат теории графов. В задаче о Кениксбергских мостах (см. рис. 1) необходимо было определить можно ли, начав с некоторой точки, совершить прогулку и вернуться в исходную точку, пройдя по каждому мосту ровно один раз. 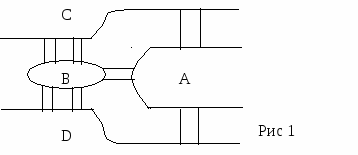 В 1930 году К. Куратовским была решена задача о трех домах и трех колодцах, сформулированная следующим образом: «Имеются три дома и три колодца. Жители домов поссорились и решили проложить дороги к своим колодцам так, чтобы они не пересекались. Возможно ли это?» Почти 100 лет не была доказана теорема о раскраске карты: «Любую карту на плоскости можно раскрасить четырьмя красками так, чтобы никакие две соседние области не были закрашены одним цветом.» Родившись при решении головоломок и занимательных игр, теория графов стала в настоящее время простым, доступным и мощным средством решения вопросов, относящихся к широкому кругу проблем. В виде графов можно интерпретировать схемы дорог и электрические цепи, географические карты и молекулы химических соединений, связи между людьми и группами людей. То есть виде графа можно изобразить любую структуру, на которой задано некоторое отношение между её объектами. На рисунках 2 и 3 изображены участок электрической цепи и часть карты дорог. Ясно, что оба эти рисунка могут быть представлены одной и той же диаграммой из точек и линий, изображенной на рисунке 4 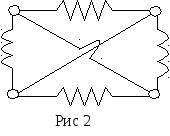 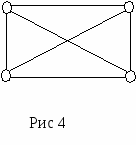 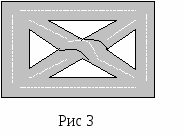 Основные определения Определение. Определим граф как совокупность двух множеств непустого множества V (множество вершин) и множества E неупорядоченных и упорядоченных пар вершин из V. Определение. Неупорядоченная пара вершин называется ребром, а упорядоченная пара - дугой. Определение. Граф, содержащий только ребра, называется неориентированным; граф, содержащий только дуги, - ориентированным, или орграфом, содержащий и ребра и дуги – смешанным. Каждый граф можно представить на плоскости множеством точек, соответствующих вершинам, которые соединены линиями, соответствующими ребрам. В трехмерном пространстве любой граф можно представить, таким образом, что линии (ребра) не будут пересекаться. Вершины графа на рисунке выделяют обычно кружочками или квадратиками, так как не всегда точки пересечения ребер являются вершинами графа. Н 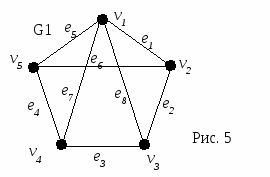 а рисунке 5 изображен неориентированный граф G1, с пятью вершинами и восьмью ребрами.На рисунках 6 и 7 изображены ориентированный и смешанный графы, соответственно. 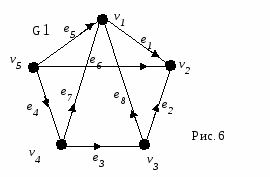 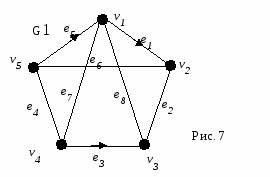 Обозначения Множество вершин будем обозначать большой латинской буквой V. Элементы этого множества (вершины) – маленькими латинскими буквами v с индексом. Множество ребер (дуг) обозначим большой латинской буквой Е, а сами ребра (дуги) - маленькими латинскими буквами е с индексом. Граф G с множеством вершин V и множеством ребер Е будем обозначать G(V,E). Количество вершин (мощность множества V) будем обозначать |V|, количество ребер (дуг) – |E|. Для графа, изображенного на рисунке 1.5 V={v1, v2, v3, v4, v5, }, |V|=5, E={e1, e2, e3, e4, e5, e6, e7, e8}, |E|=8. Определение. Вершины, соединенные ребром (дугой), называются смежными. Ребра (дуги), имеющие общую вершину, также называются смежными. Определение. Ребро и любая из его двух вершин называются инцидентными. Определение. Степень вершины в неориентированном графе - число ребер, концом которых является эта вершина. Будем обозначать степень i-той вершины через deg vi. Например, для графа, изображенного на рисунке 5:
Определение. Пусть v вершина орграфа D назовем полустепенью исхода v число дуг орграфа D, имеющих вид (v, w); аналогично полустепенью захода v назовем число дуг вида (w, v). Будем обозначать полустепень захода i-той вершины через deg+ vi, полустепень исхода i-той вершины через deg- vi. Например, для графа, изображенного на рисунке 6 deg+ v1=3, deg- v1=1. Определение. Если два ребра инцидентны одной и той же паре вершин, они называются кратными. Определение. Граф, содержащий кратные ребра называется мультиграфом.. Например, граф соответствующий ситуации, описанной в задаче о кенигсбергских мостах, является мультиграфом и изображен на рисунке 8. Ребра е1 и е2 этого графа соединяют одну и ту же пару вершин, а значит, являются кратными. 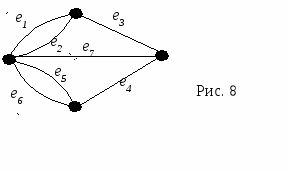 Определение. Ребро (дуга) называется петлей, если начало и конец его (её) совпадают. О 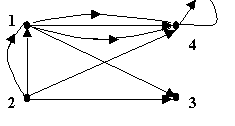 пределение. Граф содержащий петли называется псевдографом Рис. 9 На рисунке 9 изображен мульти-псевдограф. Определение. Неориентированный граф без петель и кратных ребер называется простым графом. Теорема. (Лемма о рукопожатиях). В простом графе сумма степеней всех его вершин – число четное, равное удвоенному числу ребер графа.  Доказательство. Очевидно, что каждое ребро вносит 2 в сумму степеней вершин. Теорема. Число нечетных вершин простого графа четно. Доказательство. Предположим противное: существует граф G, имеющий нечетное количество вершин нечетной степени. Подсчитаем сумму степеней всех вершин – она будет нечетной, что противоречит лемме о рукопожатиях. Орлемма о рукопожатии. Сумма полустепеней захода всех вершин орграфа равна сумме полустепеней исхода всех вершин.   Доказательство. Каждая дуга “участвует” в каждой сумме ровно один раз. Примеры графов Определение. Регулярный граф – граф, у которого все вершины имеют одну и ту же степень. 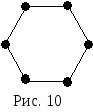 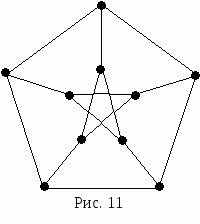 На рисунке 10 изображен регулярный граф со степенью регулярности 2. На рисунке 11 – регулярный граф со степенью регулярности 3. Граф, изображенный на рисунке 11 называют графом Петерсона, он интересен тем, что любые две его вершины соединены маршрутом, проходящим не более чем по двум ребрам. Определение. Граф называется полным, если каждые две его различные вершины соединены одним и только одним ребром. Полный граф с n вершинами обозначается Кn. На рисунке 12 изображены полные графы на 2, 3 и 5 вершинах. 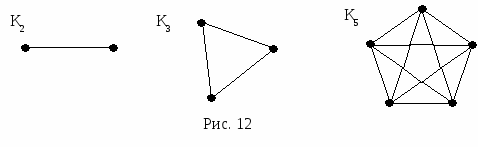 Определение. Двудольный граф-это граф G(V,E), такой что множество V разбито на два непересекающихся множества V1 и V2(  ,  ), причем всякое ребро из E соединяет вершину из V1 с вершиной из V2. Множества V1 и V2 называются долями двудольного графа. Если двудольный граф содержит все ребра, соединяющий множества V1 и V2, то он называется полным двудольным графом.Полный двудольный граф с m вершинами в одной доле и n вершинами в другой обозначается Кmn. На рисунке 13 изображен полный двудольный граф К33 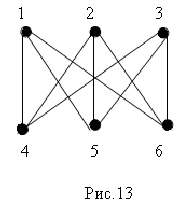 Способы описания графа. При решении задач на компьютере граф должен быть представлен дискретным способом. Известны различные способы представления графов в памяти компьютера, которые различаются объемом занимаемой памяти и скоростью выполнения операций над графами. Выбор наилучшего представления определяется требованиями задачи. При решении конкретных задач используются, как правило, некоторые комбинации или модификации указанных представлений. Матрица смежности
Для неориентированного графа A[i,j]=  Для неориентированного графа - это симметричная матрица с нулями на главной диагонали. Сумма цифр в любой строке или столбце равна степени соответствующей вершины. Ниже представлена матрица смежности графа, изображенного на рисунке 13 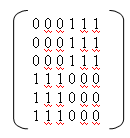 Для ориентированных графов 1 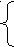 , существует дуга (i, j)A[i,j]= 0, не существует дуги вида (i, j) Для ориентированных графов матрица смежности не будет симметрична относительно главной диагонали. Для ориентированных мульти- и псевдографов A[i,j] равно количеству дуг, соединяющих вершину i с вершиной j. На рисунке 14 изображен ориентированный мульти-псевдограф и его матрица смежности 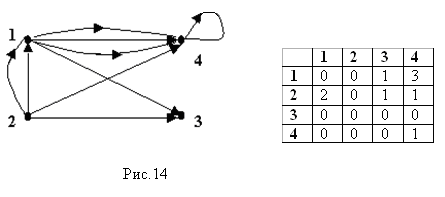 Матрица инциденцийМатрица инциденций отражает инцидентность вершин и ребер. Для неориентированных графов  1, вершина с номером i инцидентна ребру с номером j,A[i,j]= 0, вершина с номером i не инцидентна ребру с номером j. На рисунке 15 изображен простой граф и его матрица инцидентности. 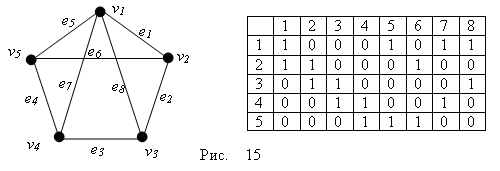 Для ориентированных графов 1, вершина с номером i инцидентна ребру с номером j и является его концом,A[i,j]= 0, вершина с номером i не инцидентна ребру с номером j, -1 вершина с номером i инцидентна ребру с номером j и является его началом. На рисунке 16 изображен орграф и его матрица инцидентности.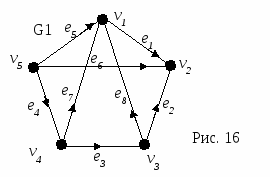 
Перечень реберДля хранения перечня ребер используют двумерный массив размерности |Е| х 2, каждая строка которого описывает ребро графа. Для графа, изображенного на рисунке 15 перечень ребер имеет вид:
Изоморфизм графов. Определение. Два графа изоморфны, если существует взаимно однозначное соответствие между их вершинами, обладающее тем свойством, что две вершины соединены ребром в одном графе тогда и только тогда, когда они соединены ребром в другом. На рисунке 17 изображены изоморфные графы. 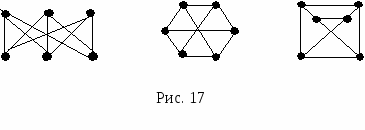 Достижимость и связность Определение. Маршрут – это последовательность ребер (дуг) графа, в которой конец каждого ребра (дуги) совпадает с началом следующего ребра. 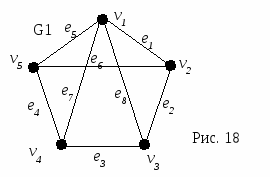 Определение. Число ребер маршрута называется его длиной. Определение. Циклом называется замкнутый маршрут. Например, в графе, изображенном на рисунке 18, вершины v5иv3 соединены маршрутами (е6, е2) длины 2; (е5, е1, е2) длины 3. Маршрут (е5, е1, е2, е3, е4) является циклом. Определение. Если существует маршрут из вершины графа v в вершину u, то говорят, что u достижима из v. |
?
?
.
.