Курсовая термех 1курс. Дано Mур Мдв 0,8 Нм 30Масса звеньев 0,5 кг 0
 Скачать 43.58 Kb. Скачать 43.58 Kb.
|
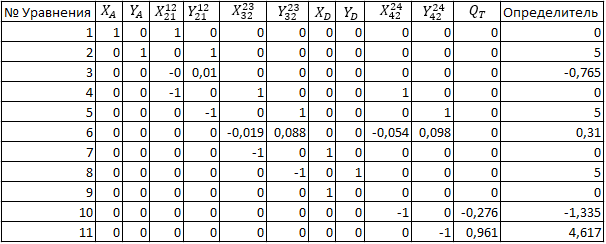 Статика. Статика.Дано: Mур =Мдв =0,8 Нм; φ 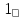 =30 =30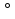 Масса звеньев: Масса звеньев: 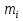 =0,5 кг; =0,5 кг; 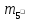 =0; =0;Веса звеньев: 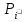 = =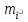 *g= 0,5*9,81 *g= 0,5*9,81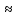 5Н. 5Н.Длины звеньев: AB=0,016м; BC=0,09 м; EH=0,072 м; СЕ=0,036 м; СD=0,05 м; EB=0,112 м; Определить: 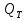 =?. =?.Решение: Освободим систему от связей, заменяя их действие реакциями. Воспользуемся способом решение задачи путем расчленения системы на отдельные звенья. При этом каждое звено должно подчиняться условиям равновесия. Записываем условия равновесия звеньев. 1 звено АВ: 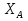 + +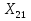 =0; (1) =0; (1)∑ 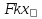 =0; =0; 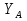 - -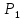 + +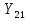 =0; =0;∑ 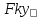 =0; =0; 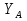 + +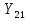 = =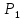 ; ; 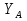 + +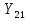 =5; (2) =5; (2)∑ 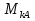 =0; Мдв- =0; Мдв-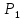 * *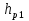 + +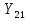 * *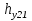 - -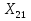 * *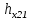 =0; =0;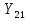 *ABcos30⁰ - *ABcos30⁰ -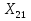 *ABsin30⁰= -Мдв + *ABsin30⁰= -Мдв +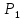 *AB *AB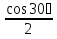 ; ;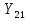 *0,016cos30⁰ - *0,016cos30⁰ -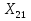 *0,016sin30⁰= -0,8+5*0,016 *0,016sin30⁰= -0,8+5*0,016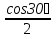 ; ;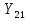 *0,014 - *0,014 -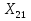 *0,008= -0,765; (3) *0,008= -0,765; (3)2 звено BCE: ∑Fkx=0; - 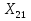 + +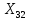 + +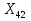 =0; (4) =0; (4)∑Fky=0; - 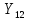 - -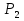 + +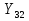 + + =0; =0;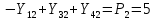 ; (5) ; (5)∑Mкв=0; 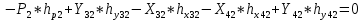 ; ;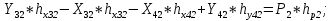 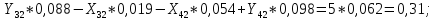 (6) (6)3 звено СD: ∑Fkx=0; 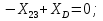 (7) (7)∑Fky=0; 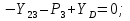 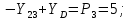 (8) (8)∑ 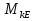 =0; =0; 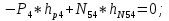 Откуда сразу можно вычислить: 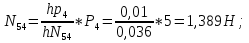 ∑Fkx=0; 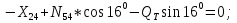 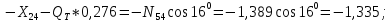 (10) (10)∑Fky=0; 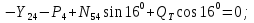 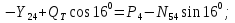 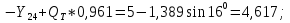 (11) (11)5 звено: ∑Fkx=0; 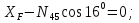 Решаем матрицу с помощью программы Mathcad U.14.0.0.163 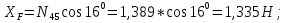 ∑Fky=0; 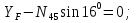 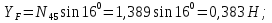 Составляем матрицу Кинематика. Дано: φ 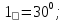 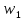 =50 рад/c; =50 рад/c;AB=0,016 м; BC=0,09 м; CE=0,036 м ; EH=0,072 м; CD=0,05 м; EB=0,112 м; 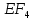 =0,036 м; =0,036 м;Решение: Определим скорость т. B: 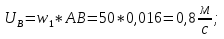 Для построения плана скоростей выберем длину вектора pb и определим масштаб скоростей 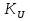 . .При pb=80мм 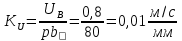 ; ;Для определения скорости т. С составим следующее векторное уравнение: 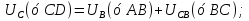 Тогда: 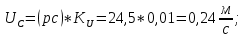 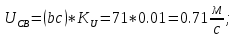 Условие скорости звеньев 2 и 3: 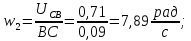 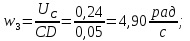 Положение т. e на плане определим по теореме подобия: 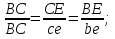 Значит: 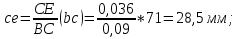 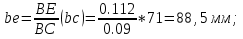 При этом 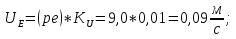 Составляем еще векторное уравнение: 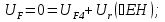 т.к т. F неподвижна; т.к т. F неподвижна;При этом: 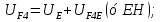 Тогда: 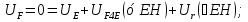 Значит: 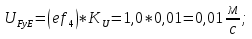 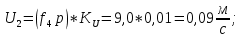 Угловая скорость звена 4: 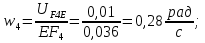 Положение т. h на плане определяем также на основании теоремы подобия: 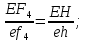 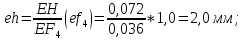 При этом: 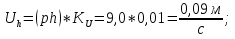 Построение плана ускорений. Поскольку 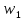 =const, то =const, то 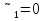 . Значит, абсолютное ускорение т. В равно ее нормальной составляющей, т.к . Значит, абсолютное ускорение т. В равно ее нормальной составляющей, т.к 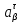 = =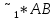 =0. =0.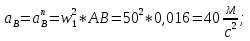 Выберем длину вектора 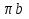 B определим масштаб ускорений B определим масштаб ускорений 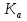 : : 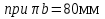 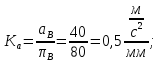 Для определения ускорения т. С составляем следующее векторное уравнение: 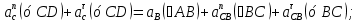 В этом уравнении: 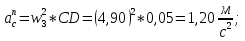 Длина вектора, изображающего это ускорение на плане: 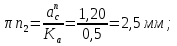 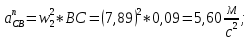 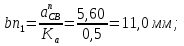 Из построения можно вычислить: 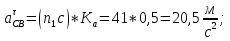 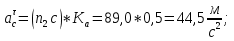 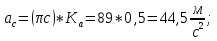 Угловые ускорения звеньев 2 и 3: 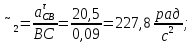 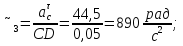 Положение т. e на плане ускорений определяется по аналогии с планом скоростей на основании теоремы подобия: 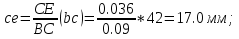 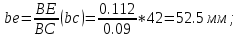 При этом: 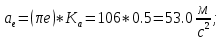 Рассматривая звенья 4 и 5 запишем еще векторные уравнения, учитывая, что т. F неподвижна: 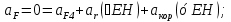 Поскольку 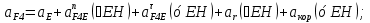 В этом уравнении: 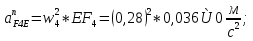 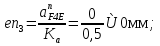 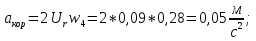 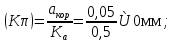 Вычисляем: 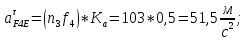 Угловое ускорение звена 4: 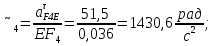 Определяем на плане положение т. h: 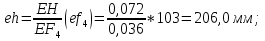 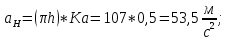 Динамика. С помощью построенного плана скоростей определяем: 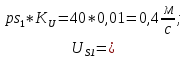 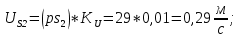 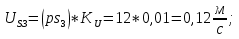 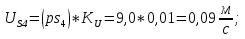 Определим кинетическую энергию механизма в данном положении. 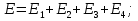 где 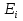 -кинетическая энергия звена механизма, Дж; -кинетическая энергия звена механизма, Дж;Кинетическая энергия кривошипа 1, совершающего вращательное движение: 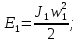 где 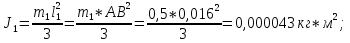 Тогда: 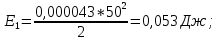 Кинетическая энергия шатуна 2, совершающего плоское движение: 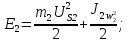 Примем 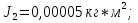 Тогда: 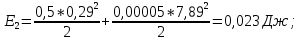 Кинетическая энергия коромысла 3, совершающего вращательное движение: 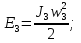 где 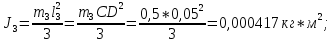 Значит: 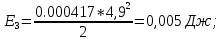 Кинетическая энергия шатуна 4, совершающего плоское движение: 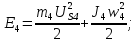 где 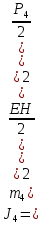 Тогда: 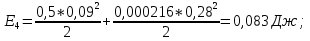 Итак: 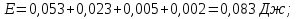 Определяем главный вектор количества движения: 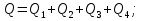 где 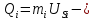 главный вектор количества движения каждого звена; главный вектор количества движения каждого звена;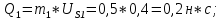 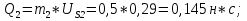 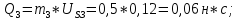 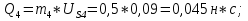 Построим план количеств движения в масштабе 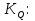 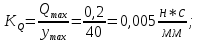 Тогда: 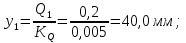 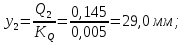 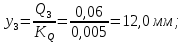 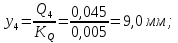 Из построения получим: 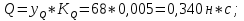 |
