спланы. Давайте вспомним что такое аппроксимация
 Скачать 0.97 Mb. Скачать 0.97 Mb.
|
|
Сплайны Сплайн-это функция или модель, предполагающая разбиение всего пространства моделирования на интервалы (сегменты или звенья сплайна) с последующим заданием какого-либо полинома (отрезка степенного ряда) в каждом сегменте.  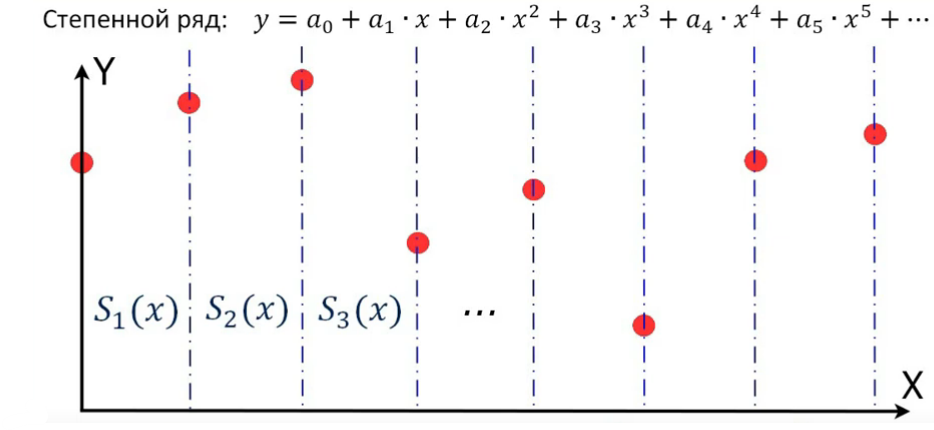 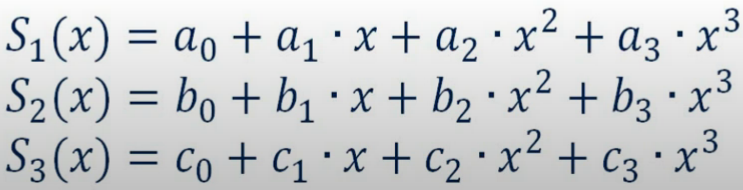 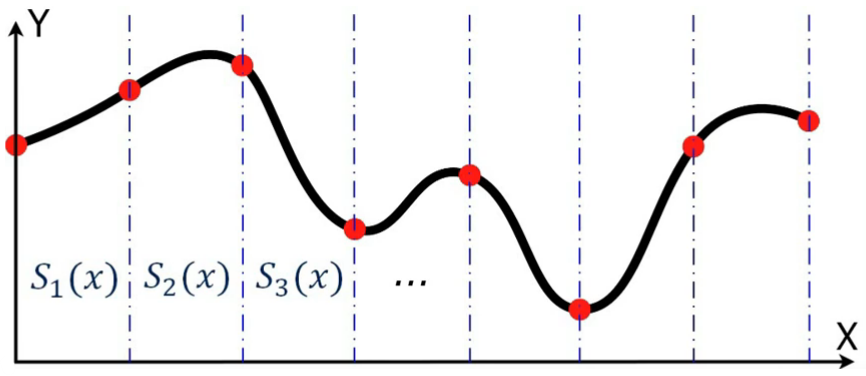 (Есть какие-то экспериментальны данные, результаты измерений, точки, которые даны нам в виде каталога координат этих точек на системе координат. Эти точки заданы в двумерном пространстве. Мы будем сводить эту задачу к одномерной задаче и получим одномерную задачу. Мы разбиваем все пространство моделирования на сегменты сплайна. Между точками находятся сегменты, в данном случае они равномерны. В каждом интервале задаем степенной ряд в какой-либо степени. В каждом интервале разбиения задаем полином какой-то степени. Например, первой степени, тогда это будут отрезки прямых. Каждый отрезок прямых kx+b или y=a0+a1*x-это тот же самый kx+b. Либо квадратичный полином, в каждом интервале свой, но чаще всего это кубический полином, в нем 4 неизвестных коэффициента. Вот пример кубического полинома, в каждом интервале задан свой полином. В первом интервале задан кубический полином и все неизвестные коэффициенты называются а, во втором b, в третьем с и т.д. На это примере получилось так, что интервал разбиения получился одинаковый, в общем случае он не одинаковый. И вот в результате решения некоторой системы уравнения мы получаем вот такую вот кривую. В каждом интервале разбиения свой полином. Вот такого вот вида (кубического) (давайте вспомним что такое аппроксимация) Аппроксимация-это замена одних математических объектов другими математическими объектами: 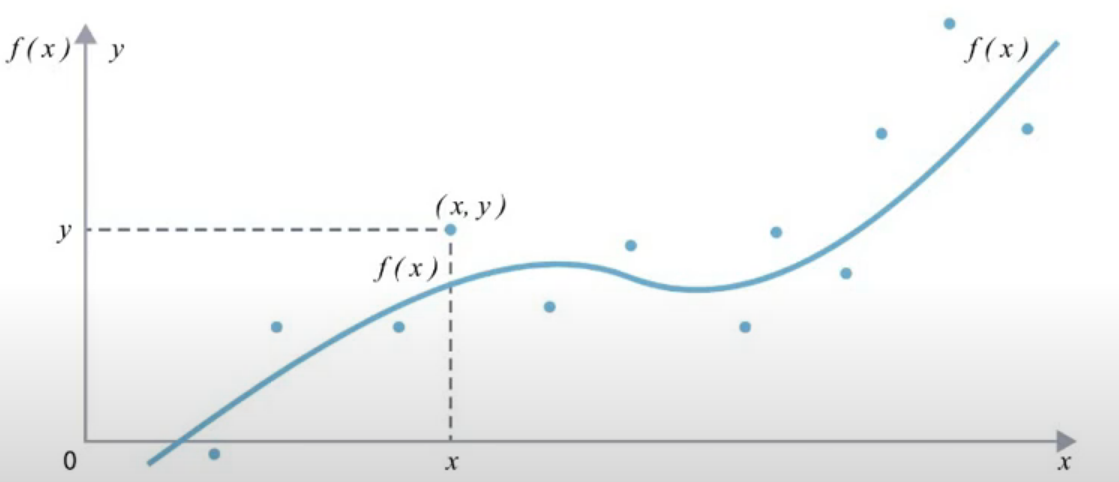 (вот были мат. объекты это точки, т е каталог координат это один мат объект, а другой мат объект это ф-ция с помощбю которой мы хотим заменить этот каталог координат. И получается мы имеем двумерную задачу (т е каталог координат х и у), а заменяем ф-цию f(x), это уже одномерная ф-ция. Заменяем один мат объект на другой) 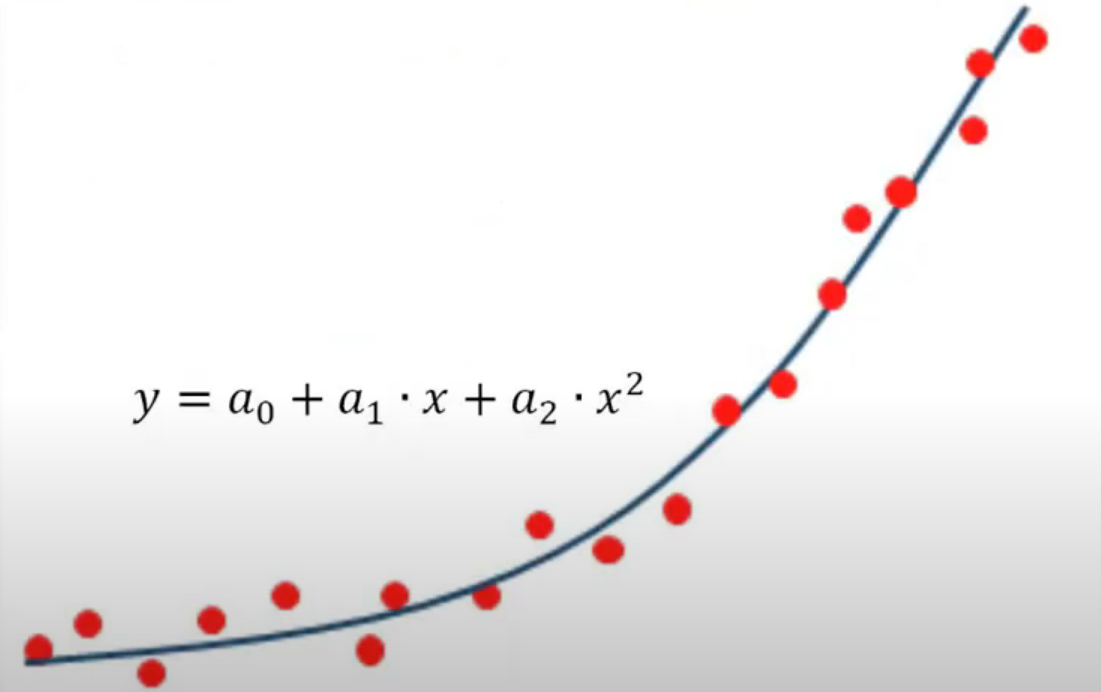 (есть ряд точек и мы заменяем вот этот каталог координат такой вот квадратичной моделью. В итоге мы получаем, что модель уклоняется от точек. Эта вот величина отклонения называется невязкой. Подбираем все эти коэффициенты под условие (сумма невязок квадратов должна быть минимальной) минимальной суммы квадратов) ( в противовес аппроксимации поговорим об инетрполяции) Интерполяция-это замена математических объектов другими. Но при этом модель (ф-ия) точно проходит через измеренные точки: 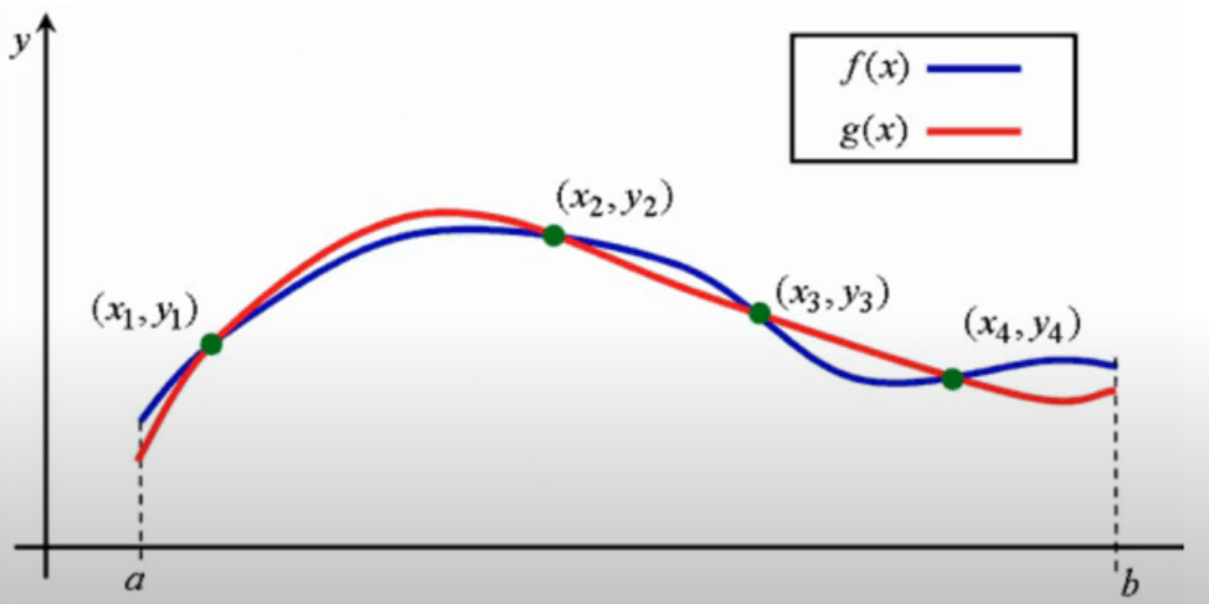 Можно говорить, что интерполяция это частный случай аппроксимации, когда все уклонения от модели равны 0 Можно утверждать, что аппроксимация-это обобщение понятия интерполяции, когда функция проходит вблизи измеримых точек: 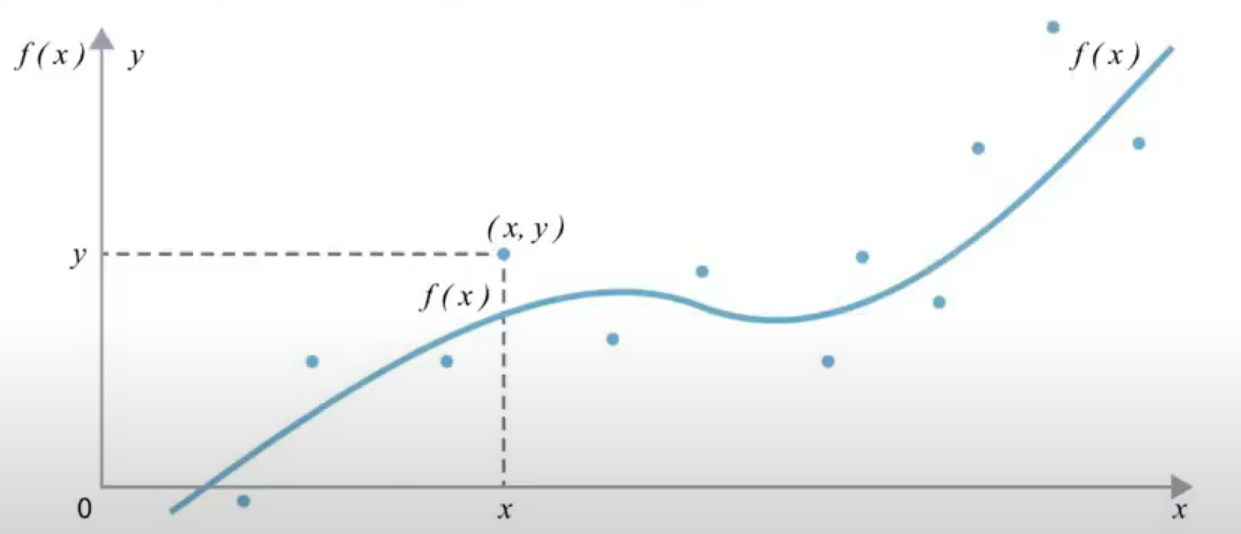 Сплайны бывают: интерполяционные и сглаживающие ( которые тесно связаны с аппроксимацией, можно еще назвать аппроксимирующие сплайны) |
