Действие учителя Цель 1 Задает вопрос Можно ли проверить перпендикулярность прямой и плоскости с помощью определения
 Скачать 1.06 Mb. Скачать 1.06 Mb.
|
|
№13. Соотнесите действие учителя с его целью во время работы с признаком перпендикулярности прямой и плоскости:
№14. Дан текст учебника. Выберите подходящий для него заголовок.  1) «О значении перпендикуляра в технике и быту». 2) «О значении перпендикуляра в законах отражения и преломления света». 3) «О значение перпендикуляра к плоскости». 4) «Перпендикулярность прямых и плоскостей как основа “строительной” геометрии». №14. Дан текст учебника. Выберите подходящий для него заголовок.   1) «О значении перпендикуляра в технике и быту». 2) «О значении перпендикуляра в законах отражения и преломления света». 3) «О значение перпендикуляра к плоскости». 4) «Перпендикулярность прямых и плоскостей как основа “строительной” геометрии». №3. Вставьте пропущенные слова в построении расстояния между скрещивающимися прямыми a и b: 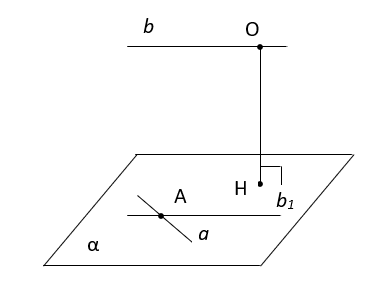 1. Через произвольную точку А на прямой _ (1) _ провести прямую b1 ll_ (2) _. 2. Через прямые a и b1 провести плоскость α ll_ (3) _. 3. Отметить произвольную точку О на прямой b. 4. Опустить перпендикуляр _ (4) _ на плоскость α.
А) b B) OH C) α D) a E) b1 №4. Дана задача: «Один конец данного отрезка лежит в плоскости α, а другой находится на расстоянии 4 см. Найдите расстояние от середины данного отрезка до плоскости α». Выберите верный чертеж к данной задаче: 1) 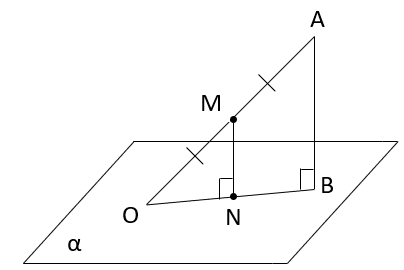 MN-искомое расстояние. MN-искомое расстояние.2) 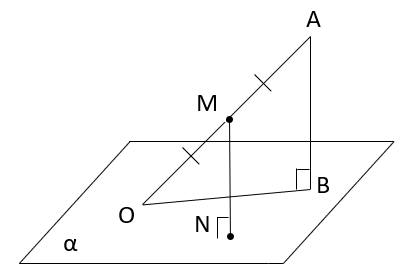 MN-искомое расстояние. MN-искомое расстояние.3) 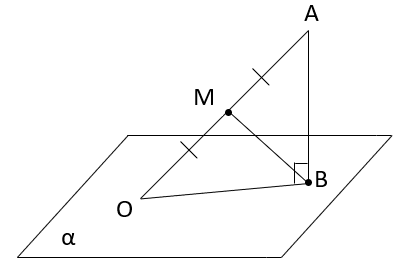 MB-искомое расстояние. MB-искомое расстояние.4) 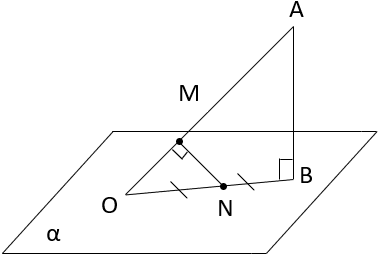 MN-искомое расстояние. MN-искомое расстояние.№5. Дана задача: «В тетраэдре ABCD точка E – середина ребра AC, AB=BC, DA=DC. Докажите, что плоскость треугольника BDE перпендикулярна к прямой AC.» 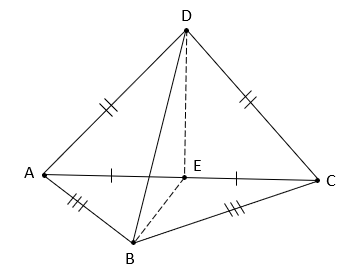 Для доказательства того, что AC⊥(BDE) по признаку перпендикулярности прямой и плоскости, ученик выбрал в плоскости (BDE) прямые DE и DB. Выясните, прав ли он, и выберите нужные прямые: 1.DEиDB. 2.BE и DB. 3.DE и BE. №6. Дана задача: «В тетраэдре ABCD точка E – середина ребра AC, AB=BC, DA=DC. Докажите, что плоскость треугольника BDE перпендикулярна к прямой AC.»  Доказав, что AC⊥DE и AC⊥BE, ученик сделал вывод, что AC⊥(BDE) по определению. Выясните, где допущена ошибка и выберите верный вариант: 1) вместо AC⊥(BDE) по определению надо AC⊥(BDE) по теореме о трех перпендикулярах. 2) вместо AC⊥DE и AC⊥BE надо AC⊥DB и AC⊥BE. 3) вместо AC⊥(BDE) по определению надо AC⊥(BDE) по признаку перпендикулярности прямой и плоскости. №7. Дано требование: доказать, что прямая перпендикулярна плоскости. Выберите из списка его верную переформулировку на основе определения прямой, перпендикулярной плоскости: 1. Доказать, что прямая перпендикулярна произвольной прямой, лежащей в этой плоскости. 2. Доказать, что прямая перпендикулярна двум параллельным прямым, лежащим в этой плоскости. 3. Доказать, что прямая перпендикулярная двум произвольным прямым, лежащим в этой плоскости. 4. Доказать, что прямая перпендикулярная двум пересекающимся прямым, лежащим в этой плоскости. №8. Вставьте пропущенные слова в схеме доказательства перпендикулярности прямой и плоскости по определению: 1) Построить произвольную _ (1) _в данной плоскости. 2) Доказать, что данная прямая _ (2) _произвольной прямой. 3) Сделать вывод, что прямая перпендикулярна _ (3) _.
А) плоскость B) плоскости C) параллельна D) перпендикулярна E) прямую F) прямой №9. Каким способом доказывается теорема: «Если одна из двух параллельных прямых перпендикулярна к плоскости, то и другая прямая перпендикулярна этой плоскости»:  1. Метод от противного. 2. Переформулировка требования. 3. Метод воображаемого построения. №10. Дано доказательство теоремы «Если две прямые перпендикулярны плоскости, то они параллельны»:  Восстановите последовательность этапов данной теоремы: 1. Доказать, что построенная прямая совпадает с данной по условию прямой. 2. Построить удовлетворяющую требованию теоремы прямую. 3. Сделать вывод, что данная прямая удовлетворяет требованию теоремы. №11. Вставьте на место пропуска недостающие данные алгоритма применения теоремы о трех перпендикулярах:  a⸦α a⸦αb ⊥ α c – наклонная а ⊥ с d – проекция наклонной ______ 1. c⊥ d 2. а ⊥ d 3. а ⊥ b 4. c ⊥ α №11. Вставьте на место пропуска недостающие данные алгоритма применения теоремы о трех перпендикулярах: если прямая, лежащая на плоскости, перпендикулярна проекции наклонной на эту плоскость, то данная прямая перпендикулярна и самой наклонной.  a⸦α a⸦αAH ⊥ α АМ – наклонная а ⊥ АМ НМ – проекция наклонной ______ 1. АМ ⊥ НМ 2. а ⊥ НМ 3. а ⊥ АН 4. АМ ⊥ α №12. Выберите алгоритм применения теоремы по ее формулировке: если плоскость проходит через перпендикуляр к другой плоскости, то эти плоскости взаимно перпендикулярны. А) 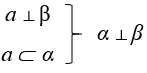 B) 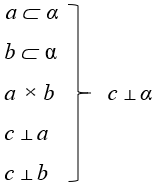 C) 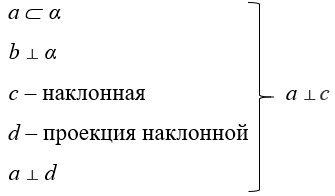 №5. Выберите алгоритм №15. При подведении итогов урока по теме «Перпендикулярность прямой и плоскости» учитель задал вопрос: «С каким новым понятием и фактом мы сегодня познакомились и что о них узнали?». Какие ответы учеников желательно услышать? 1) Формулировку признака перпендикулярности прямой и плоскости. 2) Определение расстояния от точки до плоскости. 3) Что было дано и что требовалось доказать в признаке перпендикулярности прямой и плоскости. 4) Определение наклонной, проведенной из данной точки к данной плоскости. 5) Что надо проверить, чтобы можно было применить признак перпендикулярности прямой и плоскости. 6)Этапы доказательства признака перпендикулярности прямой и плоскости. 7) Определение прямой, перпендикулярной плоскости. |
